八年级数学下册第19章矩形菱形与正方形19.3正方形作业课件新版华东师大版(共21张ppt)
文档属性
| 名称 | 八年级数学下册第19章矩形菱形与正方形19.3正方形作业课件新版华东师大版(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 696.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 09:35:52 | ||
图片预览






文档简介
(共21张PPT)
第19章 矩形、菱形与正方形
19.3 正方形
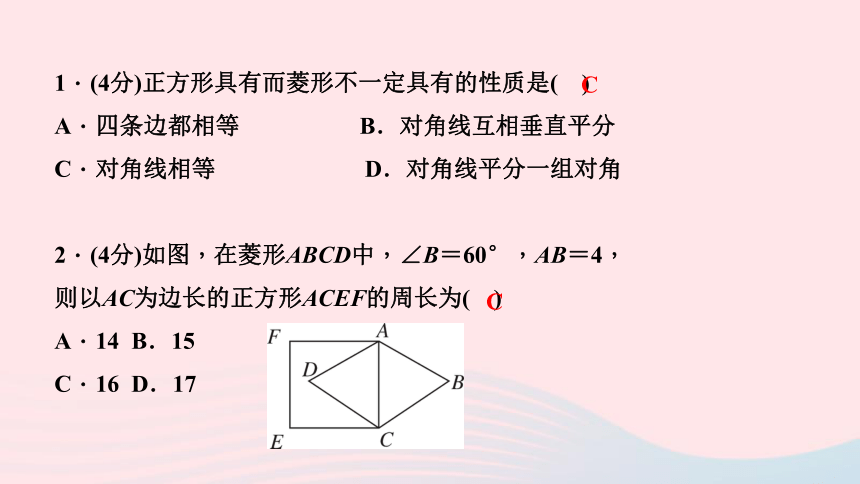
1.(4分)正方形具有而菱形不一定具有的性质是(
)
A.四条边都相等 B.对角线互相垂直平分
C.对角线相等
D.对角线平分一组对角
2.(4分)如图,在菱形ABCD中,∠B=60°,AB=4,
则以AC为边长的正方形ACEF的周长为(
)
A.14
B.15
C.16
D.17
C
C
3.(4分)如图,在正方形ABCD的外侧,作等边三角形ADE,
AC,BE相交于点F,则∠BFC为(
)
A.45°
B.55°
C.60°
D.75°
4.(4分)如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角形的直角顶点落在A点,两条直角边分别与CD交于点F,CB的延长线交于点E,则四边形AECF的面积为____.
C
16
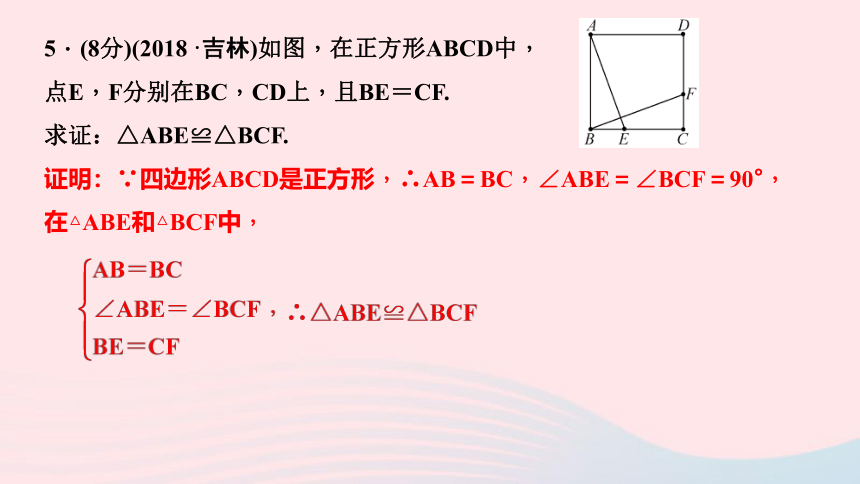
5.(8分)(2018·吉林)如图,在正方形ABCD中,
点E,F分别在BC,CD上,且BE=CF.
求证:△ABE≌△BCF.
证明:∵四边形ABCD是正方形,∴AB=BC,∠ABE=∠BCF=90°,
在△ABE和△BCF中,
6.(4分)下列说法不正确的是(
)
A.一组邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.对角线互相垂直的矩形是正方形
D.有一个角是直角的平行四边形是正方形
D
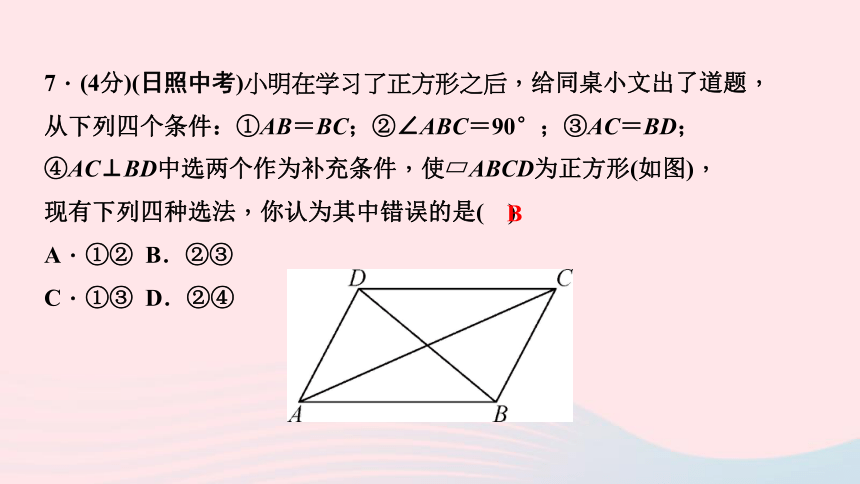
7.(4分)(日照中考)小明在学习了正方形之后,给同桌小文出了道题,
从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;
④AC⊥BD中选两个作为补充条件,使?ABCD为正方形(如图),
现有下列四种选法,你认为其中错误的是(
)
A.①②
B.②③
C.①③
D.②④
B
8.(8分)(2018·舟山)如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
解:∵四边形ABCD是矩形,∴∠B=∠D=∠C=90°,
∵△AEF是等边三角形,∴AE=AF,∠AEF=∠AFE=60°,
∵∠CEF=45°,∴∠CFE=∠CEF=45°,
∴∠AFD=∠AEB=180°-45°-60°=75°,
∴△AEB≌△AFD(AAS),∴AB=AD,∴矩形ABCD是正方形
A
A
11.(2018·武汉)以正方形ABCD的边AD作等边△ADE,
则∠BEC的度数是____________.
30°或150°
①②③
13.(12分)(2018·盐城)在正方形ABCD中,对角线BD所在的直线上
有两点E,F满足BE=DF,连结AE,AF,CE,CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.
(2)四边形AECF是菱形.理由:如图,连结AC交BD于点O,∵正方形ABCD,∴OA=OC,OB=OD,AC⊥EF,∴OB+BE=OD+DF,即OE=OF,∵OA=OC,OE=OF,∴四边形AECF是平行四边形,∵AC⊥EF,∴四边形AECF是菱形
14.(12分)(青岛中考)已知:如图,在菱形ABCD中,
点E,O,F分别为AB,AC,AD的中点,连结CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
(2)解:当AB⊥BC时,四边形AEOF是正方形,理由如下:
由(1)得AE=OE=OF=AF,∴四边形AEOF是菱形,∵AB⊥BC,OE∥BC,∴OE⊥AB,∴∠AEO=90°,∴四边形AEOF是正方形
【综合运用】
15.(16分)正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,
它的两边分别交CB,DC(或它们的延长线)于点M,N,AH⊥MN于点H.
(1)如图①,当∠MAN绕点A旋转到BM=DN时,
请你直接写出AH与AB的数量关系:________;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立,请写出理由;如果成立,请证明.
AH=AB
第19章 矩形、菱形与正方形
19.3 正方形
1.(4分)正方形具有而菱形不一定具有的性质是(
)
A.四条边都相等 B.对角线互相垂直平分
C.对角线相等
D.对角线平分一组对角
2.(4分)如图,在菱形ABCD中,∠B=60°,AB=4,
则以AC为边长的正方形ACEF的周长为(
)
A.14
B.15
C.16
D.17
C
C
3.(4分)如图,在正方形ABCD的外侧,作等边三角形ADE,
AC,BE相交于点F,则∠BFC为(
)
A.45°
B.55°
C.60°
D.75°
4.(4分)如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角形的直角顶点落在A点,两条直角边分别与CD交于点F,CB的延长线交于点E,则四边形AECF的面积为____.
C
16
5.(8分)(2018·吉林)如图,在正方形ABCD中,
点E,F分别在BC,CD上,且BE=CF.
求证:△ABE≌△BCF.
证明:∵四边形ABCD是正方形,∴AB=BC,∠ABE=∠BCF=90°,
在△ABE和△BCF中,
6.(4分)下列说法不正确的是(
)
A.一组邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.对角线互相垂直的矩形是正方形
D.有一个角是直角的平行四边形是正方形
D
7.(4分)(日照中考)小明在学习了正方形之后,给同桌小文出了道题,
从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;
④AC⊥BD中选两个作为补充条件,使?ABCD为正方形(如图),
现有下列四种选法,你认为其中错误的是(
)
A.①②
B.②③
C.①③
D.②④
B
8.(8分)(2018·舟山)如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
解:∵四边形ABCD是矩形,∴∠B=∠D=∠C=90°,
∵△AEF是等边三角形,∴AE=AF,∠AEF=∠AFE=60°,
∵∠CEF=45°,∴∠CFE=∠CEF=45°,
∴∠AFD=∠AEB=180°-45°-60°=75°,
∴△AEB≌△AFD(AAS),∴AB=AD,∴矩形ABCD是正方形
A
A
11.(2018·武汉)以正方形ABCD的边AD作等边△ADE,
则∠BEC的度数是____________.
30°或150°
①②③
13.(12分)(2018·盐城)在正方形ABCD中,对角线BD所在的直线上
有两点E,F满足BE=DF,连结AE,AF,CE,CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.
(2)四边形AECF是菱形.理由:如图,连结AC交BD于点O,∵正方形ABCD,∴OA=OC,OB=OD,AC⊥EF,∴OB+BE=OD+DF,即OE=OF,∵OA=OC,OE=OF,∴四边形AECF是平行四边形,∵AC⊥EF,∴四边形AECF是菱形
14.(12分)(青岛中考)已知:如图,在菱形ABCD中,
点E,O,F分别为AB,AC,AD的中点,连结CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
(2)解:当AB⊥BC时,四边形AEOF是正方形,理由如下:
由(1)得AE=OE=OF=AF,∴四边形AEOF是菱形,∵AB⊥BC,OE∥BC,∴OE⊥AB,∴∠AEO=90°,∴四边形AEOF是正方形
【综合运用】
15.(16分)正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,
它的两边分别交CB,DC(或它们的延长线)于点M,N,AH⊥MN于点H.
(1)如图①,当∠MAN绕点A旋转到BM=DN时,
请你直接写出AH与AB的数量关系:________;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立,请写出理由;如果成立,请证明.
AH=AB
