八年级数学下册第19章矩形菱形与正方形章末复习四作业课件新版华东师大版(共22张ppt)
文档属性
| 名称 | 八年级数学下册第19章矩形菱形与正方形章末复习四作业课件新版华东师大版(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 677.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 09:40:10 | ||
图片预览





文档简介
(共22张PPT)
第19章 矩形、菱形与正方形
章末复习(四) 矩形、菱形与正方形
1.给下列条件:①已知矩形的一边和一条对角线的长;②已知矩形的一条对角线长和两条对角线的夹角;③已知矩形的一边长及这条边与对角线的夹角;④已知矩形的周长.其中能确定矩形的形状和大小的条件是(
)
A.①②③ B.①② C.①③ D.②③
A
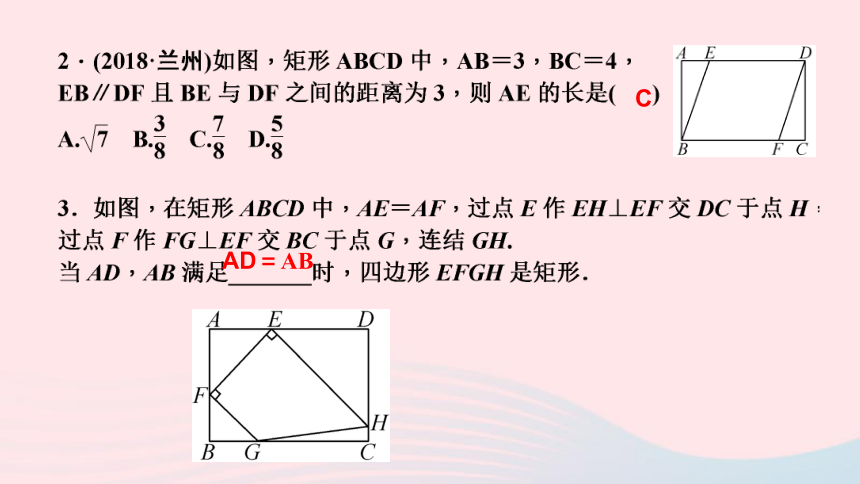
C
AD=AB
4.(2018·湘西州)如图,在矩形ABCD中,E是AB的中点,连结DE,CE.
(1)求证:△ADE≌△BCE;
(2)若AB=6,AD=4,求△CDE的周长.
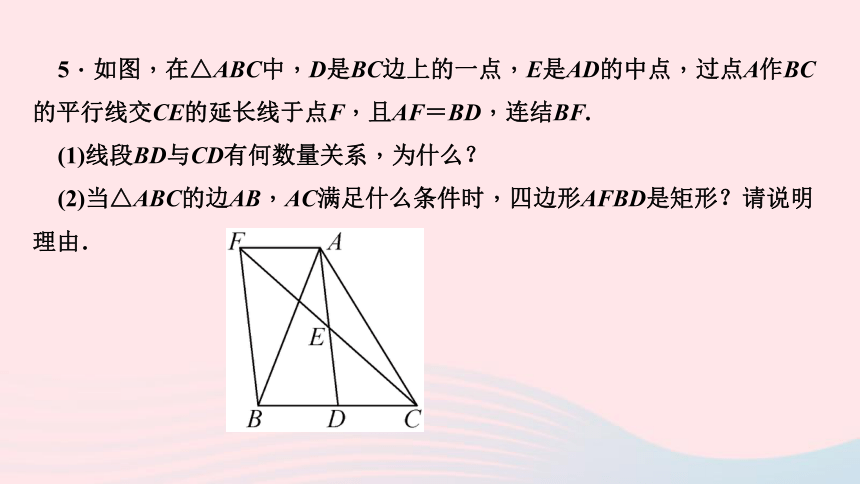
5.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连结BF.
(1)线段BD与CD有何数量关系,为什么?
(2)当△ABC的边AB,AC满足什么条件时,四边形AFBD是矩形?请说明理由.
解:(1)BD=CD.理由:∵AF∥BC,∴∠AFE=∠DCE,∠FAE=∠CDE.∵E是AD的中点,∴AE=DE,∴△AFE≌△DCE,∴AF=CD.
又AF=BD,∴BD=CD
(2)当△ABC的边AB,AC满足AB=AC时,四边形AFBD是矩形.
理由:∵AF∥BD,∴四边形AFBD是平行四边形.∵AB=AC,
BD=CD,∴AD⊥BC,∴∠ADB=90°,∴四边形AFBD是矩形
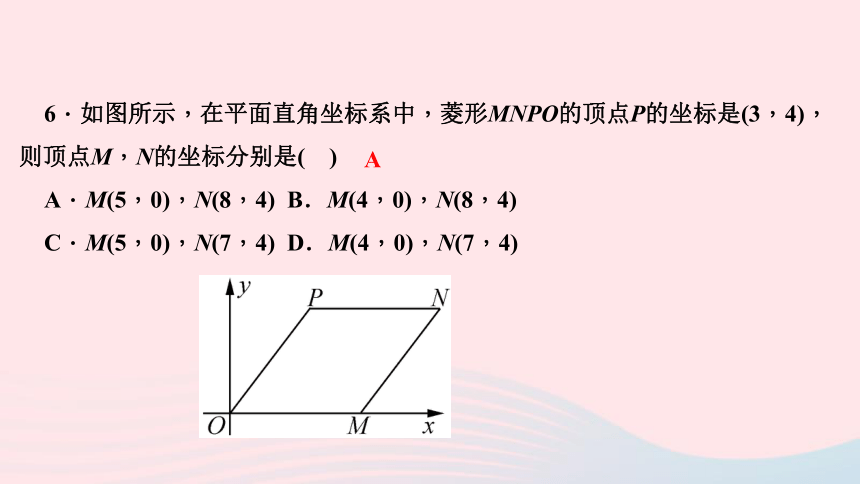
6.如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M,N的坐标分别是(
)
A.M(5,0),N(8,4)
B.M(4,0),N(8,4)
C.M(5,0),N(7,4)
D.M(4,0),N(7,4)
A
7.(临沂中考)在△ABC中,点D是边BC上的点(与B,C两点不重合),
过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,
下列说法正确的是(
)
A.若AD⊥BC,则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
D
8.(2018·黑龙江)如图,在平行四边形ABCD中,
添加一个条件______________________使平行四边形ABCD是菱形.
AB=BC或AC⊥BD等
9.如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,
垂足分别是E,F,且DE=DF.
求证:(1)△ADE≌△CDF;
(2)四边形ABCD是菱形.
(2)∵△ADE≌△CDF,∴AD=CD.
∵四边形ABCD是平行四边形,∴四边形ABCD是菱形
7.如图,在菱形ABCD中,对角线AC=6,BD=8,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,求这个最小值.
解:(1)∵AB∥CD,∴∠OAB=∠DCA,∵AC为∠DAB的平分线,∴∠OAB=∠DAC,∴∠DCA=∠DAC,∴CD=AD=AB,∵AB∥CD,∴四边形ABCD是平行四边形,∵AD=AB,∴?ABCD是菱形
11.如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以点C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是(
)
A.(2,10)
B.(-2,0)
C.(2,10)或(-2,0)
D.(10,2)或(-2,0)
C
B
13.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF是正方形的是(
)
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
D
14.如图,四边形ABCD是正方形,点E,F分别在BC,AB上,
点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,
NE⊥DE交于点N,连结NF.
(1)求证:DE⊥DM;
(2)猜想四边形CENF是怎样的特殊四边形,并证明你的猜想.
(2)四边形CENF是平行四边形.证明如下:∵四边形ABCD是正方形,
∴AB∥CD,AB=CD.∵BF=AM,∴MF=AF+AM=AF+BF=AB,
即MF=CD.又∵点F在AB上,点M在BA的延长线上,∴MF∥CD,
∴四边形CFMD是平行四边形,∴DM=CF,DM∥CF.∵NM⊥DM,
NE⊥DE,DE⊥DM,∴四边形DENM是矩形,∴EN=DM,EN∥DM,
∴CF=EN,CF∥EN,∴四边形CENF为平行四边形
第19章 矩形、菱形与正方形
章末复习(四) 矩形、菱形与正方形
1.给下列条件:①已知矩形的一边和一条对角线的长;②已知矩形的一条对角线长和两条对角线的夹角;③已知矩形的一边长及这条边与对角线的夹角;④已知矩形的周长.其中能确定矩形的形状和大小的条件是(
)
A.①②③ B.①② C.①③ D.②③
A
C
AD=AB
4.(2018·湘西州)如图,在矩形ABCD中,E是AB的中点,连结DE,CE.
(1)求证:△ADE≌△BCE;
(2)若AB=6,AD=4,求△CDE的周长.
5.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连结BF.
(1)线段BD与CD有何数量关系,为什么?
(2)当△ABC的边AB,AC满足什么条件时,四边形AFBD是矩形?请说明理由.
解:(1)BD=CD.理由:∵AF∥BC,∴∠AFE=∠DCE,∠FAE=∠CDE.∵E是AD的中点,∴AE=DE,∴△AFE≌△DCE,∴AF=CD.
又AF=BD,∴BD=CD
(2)当△ABC的边AB,AC满足AB=AC时,四边形AFBD是矩形.
理由:∵AF∥BD,∴四边形AFBD是平行四边形.∵AB=AC,
BD=CD,∴AD⊥BC,∴∠ADB=90°,∴四边形AFBD是矩形
6.如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M,N的坐标分别是(
)
A.M(5,0),N(8,4)
B.M(4,0),N(8,4)
C.M(5,0),N(7,4)
D.M(4,0),N(7,4)
A
7.(临沂中考)在△ABC中,点D是边BC上的点(与B,C两点不重合),
过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,
下列说法正确的是(
)
A.若AD⊥BC,则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
D
8.(2018·黑龙江)如图,在平行四边形ABCD中,
添加一个条件______________________使平行四边形ABCD是菱形.
AB=BC或AC⊥BD等
9.如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,
垂足分别是E,F,且DE=DF.
求证:(1)△ADE≌△CDF;
(2)四边形ABCD是菱形.
(2)∵△ADE≌△CDF,∴AD=CD.
∵四边形ABCD是平行四边形,∴四边形ABCD是菱形
7.如图,在菱形ABCD中,对角线AC=6,BD=8,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,求这个最小值.
解:(1)∵AB∥CD,∴∠OAB=∠DCA,∵AC为∠DAB的平分线,∴∠OAB=∠DAC,∴∠DCA=∠DAC,∴CD=AD=AB,∵AB∥CD,∴四边形ABCD是平行四边形,∵AD=AB,∴?ABCD是菱形
11.如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以点C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是(
)
A.(2,10)
B.(-2,0)
C.(2,10)或(-2,0)
D.(10,2)或(-2,0)
C
B
13.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF是正方形的是(
)
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
D
14.如图,四边形ABCD是正方形,点E,F分别在BC,AB上,
点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,
NE⊥DE交于点N,连结NF.
(1)求证:DE⊥DM;
(2)猜想四边形CENF是怎样的特殊四边形,并证明你的猜想.
(2)四边形CENF是平行四边形.证明如下:∵四边形ABCD是正方形,
∴AB∥CD,AB=CD.∵BF=AM,∴MF=AF+AM=AF+BF=AB,
即MF=CD.又∵点F在AB上,点M在BA的延长线上,∴MF∥CD,
∴四边形CFMD是平行四边形,∴DM=CF,DM∥CF.∵NM⊥DM,
NE⊥DE,DE⊥DM,∴四边形DENM是矩形,∴EN=DM,EN∥DM,
∴CF=EN,CF∥EN,∴四边形CENF为平行四边形
