华东师大版八年级数学下册课件:17.2.1平面直角坐标系(共36张PPT)
文档属性
| 名称 | 华东师大版八年级数学下册课件:17.2.1平面直角坐标系(共36张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 09:50:41 | ||
图片预览










文档简介
义务教育课程标准实验教科书华东师大版
1、什么是函数?
2、
函数有哪些表示方法?
3、数轴的表示方法及如何在数轴上表示点?
复习回顾
二、导入
问题:你去过电影院吗?你是怎样找到座位的。
准备一张电影票,让学生说明找到位置的方法
狮城影院电影票
22排13号
如图是一条数轴,数轴上的点与实数是一一对应的.
数轴上每个点都对应一个实数,这个实数叫做这个点在数轴上的坐标
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
点A在数轴上表示-5,怎样确定点A的位置?
A
例如,点A在数轴上的坐标是-5
知道一个点的坐标,这个点的位置就确定了
已知点B、C在数轴上的坐标分别为
-3和2.5,在数轴上标出它们的位置
注意事项:
1、点的坐标的表示方法:
(1)表示点用大写字母。
(2)先写横坐标,再写纵坐标,中间用逗号分开,再用小括号把两坐标括起来。
(3)横坐标、纵坐标的位置不能颠倒。
2、知道点的位置,如何确定点的坐标:
先点已知点P分别作x轴、y轴的垂线段,垂足分别为a、b,则点P的坐标为(a,b)
点拨
1.如图,找一点P(3,2),
这时作PM⊥x轴,PN⊥y轴垂足分别为M和N,点M在x轴上对应的数是3,称为点P的横坐标,点N在y轴上对应的数2,称为点P的纵坐标。请在直角坐标系中标出点P(3,2)
1
2
3
4
-1
-2
-3
-4
1
2
3
-1
-2
-3
第一象限
第二象限
第三象限
第四象限
x
y
o
P
N
M
·
·
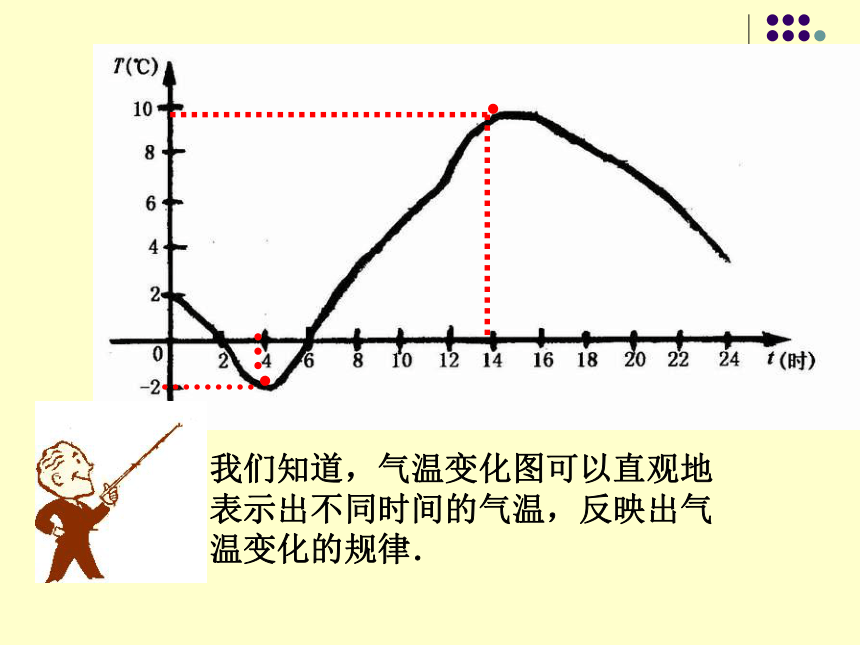
我们知道,气温变化图可以直观地
表示出不同时间的气温,反映出气
温变化的规律.
一般地,函数常常可以用它的图象来表示,利用函数的图象可以帮助我们直观地研究函数.那么,什么是函数的图象?怎样画出函数的图象呢?这一节我们将对此作一些初步的研究.为此,先学习一个非常有用的工具——
平面直角坐标系
李林
妈妈要去学校给李林开家长会,李林告诉妈妈他的座位是从门口开始数第三行第四列,妈妈从来没去过李林的教室,她根据李林的叙述能找到李林的座位吗?
门口
找座位时,先找到第几排再找到第几列就可了.
也就是说,李林的座位完全可以由两个数确定下来.
在平面上画两条原点重合、
互相垂直且具有相同单位长度的
数轴,这就建立了平面直角坐标
系。
一个平面上有无数个点,如何来确定这些点的位置呢?在数学中,我们可以用有序实数对来
确定平面上点的位置.
新授
1
2
3
﹣1
﹣2
﹣3
Y
通常把其中水平的一条数轴
叫做x轴或横轴,取向右为正方
向;
O
1
2
X
-1
-2
(横轴)
(纵轴)
铅直的数轴叫做y轴或纵轴,
取向上为正方向;
Y
两数轴的交点O叫做坐标原点.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
X轴上的坐标
写在前面
如图,平面上任意一点A,从点A分别向x轴和y轴作垂线,垂足分别为点M和点N.
·
A
M
N
A
依次写出点A的横坐标和纵坐标,
得到一对有序实数(3,2),称为
点A的坐标.记作A(3,2).
这时,点M在x轴上对应的数
为3,称为点A的横坐标;点N在y轴上
对应的数为2,称为点A的纵坐标.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
第一象限
第四象限
第三象限
第二象限
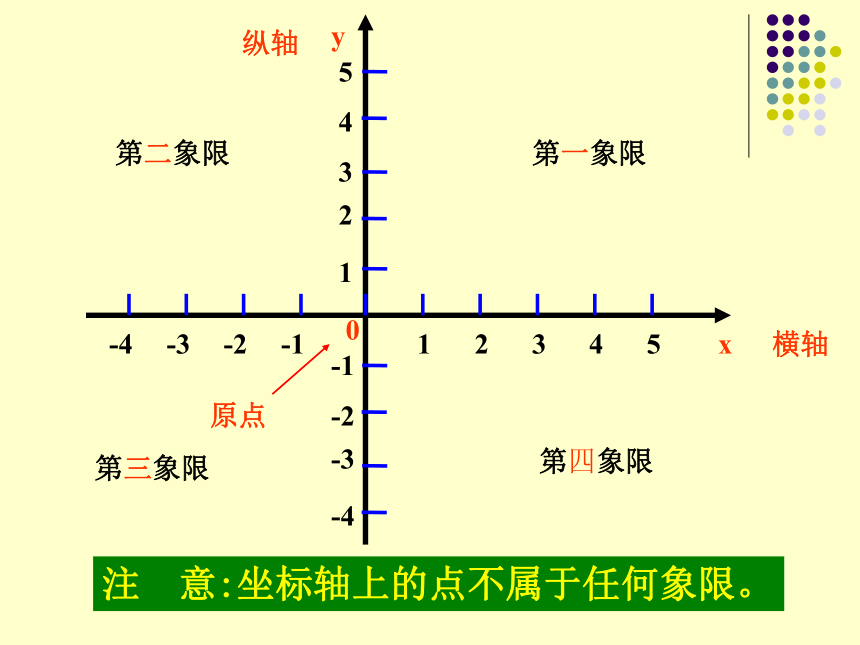
注
意:坐标轴上的点不属于任何象限。
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
(
2,3
)
(
3,2
)
(
-2,1
)
(
-4,-
3
)
(
1,-
2
)
坐标是有序
的实数对。
例1、写出图中A、B、C、D、E、F各点的坐标。
·
F
(
4,0
)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B
·
A
·
D
·
C
例2、在直角坐标系中,描出下列各点:A(4,3),
B(-2,3),C(-4,-1),D(2,-2)。
x
横轴
y
纵轴
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
第一象限
第四象限
第三象限
第二象限
(+,+)
(-,+)
(+,-)
(-,-)
平面直角坐标系内点的坐标特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
在第一象限
在第三象限
在第三象限
在第四象限
在y轴上
F(-5,1) G(6,0)
在第二象限
在x轴上
根据点所在的位置,用“+”“-”或“0”填表.
点的位置
横坐标符号
纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在x轴上
在正半轴上
在负半轴上
在y轴上
在正半轴上
在负半轴上
原点
+
-
-
-
+
0
+
-
0
+
0
-
0
0
0
-
+
+
+
例3:已知点M(
a+1,
2-a
)的位置在第一象限,
求
a的取值范围.
解:因为点M(
a+1,
2-a
)在第一象限
所以
解得
﹣1<a<2
三、例题讲解与练习
例4:若m为整数,点P(
3m-9,
3-3m
)是
第三象限的点,求P点的坐标。
解:因为点P(
3m-9,
3-3m
)是第三象限的点
解得
1
<
m
<
3
所以
又因为m为整数,
所以
m
=
2
所以
P
(﹣3
,
﹣3
)
三、例题讲解与练习
例5:已知点P(
0,
a
)在y轴的负半轴上,
则点Q(﹣a2-1,
﹣a+1)在第几象限?
解:因为点P(
0,
a
)在y轴负半轴
所以
a﹤0,
又因为a2≥0,
所以﹣a2-1﹤0
所以点Q在第二象限
﹣a+1﹥0
则a2+1﹥0
三、例题讲解与练习
例6、已知:点
P(x-2,
3x-9)在第四象限,
化简
+
解:∵点
P(x-2,
3x-9)在第四象限
∴
解得
∴
=
=
=
一、选择题
A.第一象限
B.第二象限
C.第三象限
D.第四象限
1.若
,则点P
应在(
)
2.在平面直角坐标系中,点P
一定在
(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
A.点B与C的横坐标相等
B.点B与C的纵坐标相等
C.点B与C的横坐标与纵坐标分别相等
D.点B与C的横坐标、纵坐标都不相等
3.在平面直角坐标系中,线段BC∥
轴,则
(
)
A.原点
B.
轴上
C.
轴上
D.
轴或
轴上
4.若点P
的坐标满足
,则点P必在
(
)
5.平面上的点(2,-1)通过上下平移不能与之重合的是(
)
A.(2,-2)
B.(-2,-1)
C.(2,0)
D.(2,-3)
A.(-1,-5)
B.(-1,-1)
C.(5,-1)
D.(5,5)
6.点P(2,-3)先向上平移2个单位长度,再向
左平移3个单位长度,得到点P
的坐标是(
)
二、填空题
7.将点M(2,-3)向左平移2个单位长度,再向平移
1个单位长度,得到的点的坐标为_______
8.在直角坐标系中,若点P
在
则点P的坐标为____________
轴上,
9.已知点P
,Q
,且PQ∥
轴,则
_________,
___________
10.点P
在第四象限,则点Q
在第___象限
1
A
x
y
2
3
4
1
2
3
4
-1
-2
-3
-4
-4
-3
-2
-1
0
B
P
D
C
B(-a,b)
A(a,b)
关于y轴对称
1
A
x
y
2
3
4
1
2
3
4
-1
-2
-3
-4
-4
-3
-2
-1
0
c(a,
-
b)
A(a,b)
关于x轴对称
C
P
E
F
1
(a,b)
x
y
点(a,b)
2
3
4
1
2
3
4
-1
-2
-3
-4
-4
-3
-2
-1
0
(-a,b)
(a,-b)
点(a,-b)
点(-a,b)
关于
轴对称
x
点(a,b)
关于y轴对称
简单的说:关于什么轴对称,就什么坐标不变。
0
1
-1
1
-1
x
y
P(a,b)
A(a,-b)
B(-a,b)
C(-a,-b)
对称点的坐标
(1)点(1,-3)关于X轴的对称点的坐标为______关于Y轴的对称点的坐标为_________,关于原点对称的点的坐标为
_________。
(2)点(-1,3)关于X轴的对称点的坐标为________,关于Y轴对称点的坐标为______,关于原点的对称点的坐标为____________。
一般地,点P(a,b),关于x轴对称点的坐标为
________,关于y轴对称点的坐标为_________,关于原点的坐标为_____。
(1,3)
(-1,-3)
(-1,3)
(-1,-3)
(1,3)
(1,-3)
(a,-b)
(-a,b)
(-a,-b)
(文字表述参见课本138页).
举一反三我能行!
已知点A和点B的坐标,请你根据坐标判断A、B关于x轴对称,还是关于y轴对称。
(1)A(-3,1.5)
B(3,1.5)
(2)
A(-3,-1.5)
B(-3,1.5)
(3)
A(3,1.5)
B(3,-1.5)
(4)
A(3,1.5)
B(-3,1.5)
0
1
-1
1
-1
x
y
特殊点的坐标
(x,0)
(0,y)
在平面直角坐标系内描出
(-2,2),(0,2),(2,2),(4,2),依次连接各点,从中你发现了什么?
平行于x轴的直线上的各点的纵坐标相同,横坐标不同.
平行于y轴的直线上的各点的横坐标相同,纵坐标不同.
在平面直角坐标系内描出(-2,3),
(-2,2),(-2,0),(-2,-2),依次连接各点,从中你发现了什么?
点到坐标轴及原点的距离
x
y
0
A
B
C
D
(a,b)
(-a,b)
(-a,-b)
(a,-b)
a
b
a
b
a
a
a
b
b
b
(1)写出图中的平行四边形ABCD各个顶点的坐标.
(2)图中A与D,B与C的纵坐标相同吗?
为什么?
(3)A与B,C与D的横坐标相同吗?为什么?
做一做:
x
y
0
1
1
A
B
C
D
(-2,3)
(-3,-1)
(3,-1)
(4,3)
本节课我们学面直角坐标系。学习本节
我们要掌握以下三方面的内容:
1、能够正确画出直角坐标系。
2、能在直角坐标系中,根据坐标找出点,
由点求出坐标。
3、掌握x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
4、掌握各象限内点的坐标符号特征
小结:
作业
课本第37页
习题18.2
第2、3题
1、什么是函数?
2、
函数有哪些表示方法?
3、数轴的表示方法及如何在数轴上表示点?
复习回顾
二、导入
问题:你去过电影院吗?你是怎样找到座位的。
准备一张电影票,让学生说明找到位置的方法
狮城影院电影票
22排13号
如图是一条数轴,数轴上的点与实数是一一对应的.
数轴上每个点都对应一个实数,这个实数叫做这个点在数轴上的坐标
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
点A在数轴上表示-5,怎样确定点A的位置?
A
例如,点A在数轴上的坐标是-5
知道一个点的坐标,这个点的位置就确定了
已知点B、C在数轴上的坐标分别为
-3和2.5,在数轴上标出它们的位置
注意事项:
1、点的坐标的表示方法:
(1)表示点用大写字母。
(2)先写横坐标,再写纵坐标,中间用逗号分开,再用小括号把两坐标括起来。
(3)横坐标、纵坐标的位置不能颠倒。
2、知道点的位置,如何确定点的坐标:
先点已知点P分别作x轴、y轴的垂线段,垂足分别为a、b,则点P的坐标为(a,b)
点拨
1.如图,找一点P(3,2),
这时作PM⊥x轴,PN⊥y轴垂足分别为M和N,点M在x轴上对应的数是3,称为点P的横坐标,点N在y轴上对应的数2,称为点P的纵坐标。请在直角坐标系中标出点P(3,2)
1
2
3
4
-1
-2
-3
-4
1
2
3
-1
-2
-3
第一象限
第二象限
第三象限
第四象限
x
y
o
P
N
M
·
·
我们知道,气温变化图可以直观地
表示出不同时间的气温,反映出气
温变化的规律.
一般地,函数常常可以用它的图象来表示,利用函数的图象可以帮助我们直观地研究函数.那么,什么是函数的图象?怎样画出函数的图象呢?这一节我们将对此作一些初步的研究.为此,先学习一个非常有用的工具——
平面直角坐标系
李林
妈妈要去学校给李林开家长会,李林告诉妈妈他的座位是从门口开始数第三行第四列,妈妈从来没去过李林的教室,她根据李林的叙述能找到李林的座位吗?
门口
找座位时,先找到第几排再找到第几列就可了.
也就是说,李林的座位完全可以由两个数确定下来.
在平面上画两条原点重合、
互相垂直且具有相同单位长度的
数轴,这就建立了平面直角坐标
系。
一个平面上有无数个点,如何来确定这些点的位置呢?在数学中,我们可以用有序实数对来
确定平面上点的位置.
新授
1
2
3
﹣1
﹣2
﹣3
Y
通常把其中水平的一条数轴
叫做x轴或横轴,取向右为正方
向;
O
1
2
X
-1
-2
(横轴)
(纵轴)
铅直的数轴叫做y轴或纵轴,
取向上为正方向;
Y
两数轴的交点O叫做坐标原点.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
X轴上的坐标
写在前面
如图,平面上任意一点A,从点A分别向x轴和y轴作垂线,垂足分别为点M和点N.
·
A
M
N
A
依次写出点A的横坐标和纵坐标,
得到一对有序实数(3,2),称为
点A的坐标.记作A(3,2).
这时,点M在x轴上对应的数
为3,称为点A的横坐标;点N在y轴上
对应的数为2,称为点A的纵坐标.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
第一象限
第四象限
第三象限
第二象限
注
意:坐标轴上的点不属于任何象限。
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
(
2,3
)
(
3,2
)
(
-2,1
)
(
-4,-
3
)
(
1,-
2
)
坐标是有序
的实数对。
例1、写出图中A、B、C、D、E、F各点的坐标。
·
F
(
4,0
)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B
·
A
·
D
·
C
例2、在直角坐标系中,描出下列各点:A(4,3),
B(-2,3),C(-4,-1),D(2,-2)。
x
横轴
y
纵轴
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
第一象限
第四象限
第三象限
第二象限
(+,+)
(-,+)
(+,-)
(-,-)
平面直角坐标系内点的坐标特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
在第一象限
在第三象限
在第三象限
在第四象限
在y轴上
F(-5,1) G(6,0)
在第二象限
在x轴上
根据点所在的位置,用“+”“-”或“0”填表.
点的位置
横坐标符号
纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在x轴上
在正半轴上
在负半轴上
在y轴上
在正半轴上
在负半轴上
原点
+
-
-
-
+
0
+
-
0
+
0
-
0
0
0
-
+
+
+
例3:已知点M(
a+1,
2-a
)的位置在第一象限,
求
a的取值范围.
解:因为点M(
a+1,
2-a
)在第一象限
所以
解得
﹣1<a<2
三、例题讲解与练习
例4:若m为整数,点P(
3m-9,
3-3m
)是
第三象限的点,求P点的坐标。
解:因为点P(
3m-9,
3-3m
)是第三象限的点
解得
1
<
m
<
3
所以
又因为m为整数,
所以
m
=
2
所以
P
(﹣3
,
﹣3
)
三、例题讲解与练习
例5:已知点P(
0,
a
)在y轴的负半轴上,
则点Q(﹣a2-1,
﹣a+1)在第几象限?
解:因为点P(
0,
a
)在y轴负半轴
所以
a﹤0,
又因为a2≥0,
所以﹣a2-1﹤0
所以点Q在第二象限
﹣a+1﹥0
则a2+1﹥0
三、例题讲解与练习
例6、已知:点
P(x-2,
3x-9)在第四象限,
化简
+
解:∵点
P(x-2,
3x-9)在第四象限
∴
解得
∴
=
=
=
一、选择题
A.第一象限
B.第二象限
C.第三象限
D.第四象限
1.若
,则点P
应在(
)
2.在平面直角坐标系中,点P
一定在
(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
A.点B与C的横坐标相等
B.点B与C的纵坐标相等
C.点B与C的横坐标与纵坐标分别相等
D.点B与C的横坐标、纵坐标都不相等
3.在平面直角坐标系中,线段BC∥
轴,则
(
)
A.原点
B.
轴上
C.
轴上
D.
轴或
轴上
4.若点P
的坐标满足
,则点P必在
(
)
5.平面上的点(2,-1)通过上下平移不能与之重合的是(
)
A.(2,-2)
B.(-2,-1)
C.(2,0)
D.(2,-3)
A.(-1,-5)
B.(-1,-1)
C.(5,-1)
D.(5,5)
6.点P(2,-3)先向上平移2个单位长度,再向
左平移3个单位长度,得到点P
的坐标是(
)
二、填空题
7.将点M(2,-3)向左平移2个单位长度,再向平移
1个单位长度,得到的点的坐标为_______
8.在直角坐标系中,若点P
在
则点P的坐标为____________
轴上,
9.已知点P
,Q
,且PQ∥
轴,则
_________,
___________
10.点P
在第四象限,则点Q
在第___象限
1
A
x
y
2
3
4
1
2
3
4
-1
-2
-3
-4
-4
-3
-2
-1
0
B
P
D
C
B(-a,b)
A(a,b)
关于y轴对称
1
A
x
y
2
3
4
1
2
3
4
-1
-2
-3
-4
-4
-3
-2
-1
0
c(a,
-
b)
A(a,b)
关于x轴对称
C
P
E
F
1
(a,b)
x
y
点(a,b)
2
3
4
1
2
3
4
-1
-2
-3
-4
-4
-3
-2
-1
0
(-a,b)
(a,-b)
点(a,-b)
点(-a,b)
关于
轴对称
x
点(a,b)
关于y轴对称
简单的说:关于什么轴对称,就什么坐标不变。
0
1
-1
1
-1
x
y
P(a,b)
A(a,-b)
B(-a,b)
C(-a,-b)
对称点的坐标
(1)点(1,-3)关于X轴的对称点的坐标为______关于Y轴的对称点的坐标为_________,关于原点对称的点的坐标为
_________。
(2)点(-1,3)关于X轴的对称点的坐标为________,关于Y轴对称点的坐标为______,关于原点的对称点的坐标为____________。
一般地,点P(a,b),关于x轴对称点的坐标为
________,关于y轴对称点的坐标为_________,关于原点的坐标为_____。
(1,3)
(-1,-3)
(-1,3)
(-1,-3)
(1,3)
(1,-3)
(a,-b)
(-a,b)
(-a,-b)
(文字表述参见课本138页).
举一反三我能行!
已知点A和点B的坐标,请你根据坐标判断A、B关于x轴对称,还是关于y轴对称。
(1)A(-3,1.5)
B(3,1.5)
(2)
A(-3,-1.5)
B(-3,1.5)
(3)
A(3,1.5)
B(3,-1.5)
(4)
A(3,1.5)
B(-3,1.5)
0
1
-1
1
-1
x
y
特殊点的坐标
(x,0)
(0,y)
在平面直角坐标系内描出
(-2,2),(0,2),(2,2),(4,2),依次连接各点,从中你发现了什么?
平行于x轴的直线上的各点的纵坐标相同,横坐标不同.
平行于y轴的直线上的各点的横坐标相同,纵坐标不同.
在平面直角坐标系内描出(-2,3),
(-2,2),(-2,0),(-2,-2),依次连接各点,从中你发现了什么?
点到坐标轴及原点的距离
x
y
0
A
B
C
D
(a,b)
(-a,b)
(-a,-b)
(a,-b)
a
b
a
b
a
a
a
b
b
b
(1)写出图中的平行四边形ABCD各个顶点的坐标.
(2)图中A与D,B与C的纵坐标相同吗?
为什么?
(3)A与B,C与D的横坐标相同吗?为什么?
做一做:
x
y
0
1
1
A
B
C
D
(-2,3)
(-3,-1)
(3,-1)
(4,3)
本节课我们学面直角坐标系。学习本节
我们要掌握以下三方面的内容:
1、能够正确画出直角坐标系。
2、能在直角坐标系中,根据坐标找出点,
由点求出坐标。
3、掌握x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
4、掌握各象限内点的坐标符号特征
小结:
作业
课本第37页
习题18.2
第2、3题
