华东师大版八年级数学下册课件:17.4.1反比例函数定义(共24张PPT)
文档属性
| 名称 | 华东师大版八年级数学下册课件:17.4.1反比例函数定义(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 903.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 12:46:42 | ||
图片预览








文档简介
反比例函数定义
第一课时
学习目标
1.经历从实际问题抽象出反比例函数的探索过程,发展学生的抽象思维能力。
2.理解反比例函数的概念,会列出实际问题的反比例函数关系式。
自主学习
自学课本54—55页内容。
1、体育课上,同学们跑800米时,每个同学跑步的平均速度v(单位:m/分)随着此同学跑完全程的时间t(单位:h分)的变化而变化,用含t的式子表示v.
2、一次数学课上,老师要同学们画一个面积为10平方厘米的矩形,同学们画后发现矩形相邻两边y(单位:厘米)随着x(单位:厘米)的变化而变化,用含x的式子表示y.
3、已知北京市的总面积为16800平方千米,人均占有土地面积s(单位:平方千米/人)随着全市总人口n(单位:人)的变化而变化,用含n的式子表示s.
以上三个问题的函数解析式为:
1、v=
2、y=
3、s=
小结:判断解析式是不是反比例函数,
看式子是否可以写成
的结构
思考:如何求反比例的解析式呢?
小结2:求反比例函数的解析式只需要找到一个点带入解析式就可以求出k值
小结:
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
函数定义:
一般地,在一个变化过程中,如果有两个变量x和y,
并且对于x的每一个给定的值,
y都有唯一的一个值与其相应,那么我们就说x是自变量,y是x的函数。
y=2x+3
y=10x
y=-4x
一次函数定义
一般地,形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数
当b=0时,即y=kx,是正比例函数
是一种特殊的一次函数.
回顾与思考
探究思考:
4、电流I,电阻R,电压U之间满足U=IR,当U=220
v时,你能用含R的代数式表示I吗?变量I是R的函数吗?
一般地,如果两个变量x,y之间的关系可以表示
成:
(K为常数,且K不为0)的形式,那么
称y是x的反比例函数.
注意:
1.常数
2.自变量x不能为零(因为分母为零时,该分式无意义)
3.当
可以写成
时注意x的指数为
4.注意分母是单项式
亦可表示为xy=k,y=kx-1
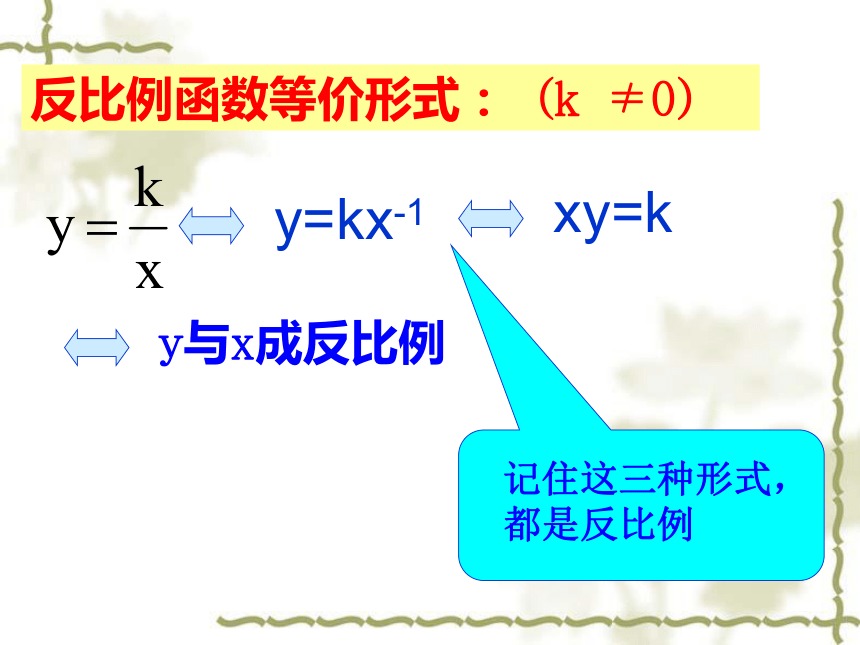
反比例函数等价形式:(k
≠0)
y=kx-1
xy=k
y与x成反比例
记住这三种形式,都是反比例
定义应用1:下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?
可以改写成
,所以y是x的反比例函数,比例系数k=1。
不具备
的形式,所以y不是x的反比例函数。
y是x的反比例函数,比例系数k=4。
不具备
的形式,所以y不是x的反比例函数。
可以改写成
所以y是x的
反比例函数,比例系数k=
随堂练习:挑战自我
1.在下列函数表达式中,x均为自变量,哪些是反比例函数?每一个反比例函数相应的k值是多少?
(b为常数)
提高练习1:关系式xy+4=0中y是x的反比例函数吗?若是,比例系数k等于多少?若不是,请说明理由。
xy+4=0可以改写成
比例系数k等于-4
所以y是x的反比例函数
反比例等价形式:(k
≠0)
y=kx-1
xy=k
反比例要点:
1、三种写法形式
2、k不等于0(注:k可以是个分数,在分母上)
2、x的次数为-1
1、已知函数
是正比例函数,则
m
=
___
2、
已知函数
是反比例函数,则
m
=
___
。
2
-3
(例2)知识点应用:次数为-1,k不为0
1.若函数y=2x
是反比例函数,
则n_____;
2.若函数y=(m+3)x
是反比例函数,
则m=_____;
n-1
lml-4
=0
3
尝试练习3:
求反比例的解析式
就是求出
k值为多少
例3:已知y是x的反比例函数,当x=2时,y=6.
(1)写出y与x的函数关系式:
(2)求当x=4时y的值.
已知y是x的反比例函数,当x=2时,y=6.
写出y与x的函数关系式:
求当x=4时y的值.
因为当
x=2
时y=6,所以有
∵y与x的函数关系式为
⑵
把
x=4
代入
得
待定系数法求
尝试练习4
(1).写出这个反比例函数的表达式;
解:∵
y是x的反比例函数,
(2).根据函数表达式完成上表.
2
-4
1
一反比例要点:
1、三种写法形式
2、k不等于0(注:k可以是个分数,在分母上)
3、x的次数为-1
二、求反比例解析式:求反比例函数的解析式只需要找到一个点带入解析式就可以求出k值
1.下列函数中哪些是反比例函数,并指出相应k的值?
①
②
③
④
⑤
⑥
⑦
⑧
(9)
xy
=
5
(10)
y
=
3x-1
y
=
2x2
y
=
2x
3
y
=
x
1
y
=
3x
y
=
3
2x
y
=
1
3x
y
=
x
1
【达标检测】
1.已知函数y=3xm-7是正比例数,m=
,
2.
.已知函数y=3xm-7是反比例函数,则
m=
.
3、已知y=(m+2)x|m|-3是反比例函数,则m=____
4、反比例函数经过(-2,3),则反比例函数的解析式为_____,
5、反比例函数,当x=2.5时,y=4,则反比例函数的解析式为_____.
6、已知y
是2x-3
成反比例,当x=
时,y=-2,写出y与x的函数关系式
反比例函数定义
第一课时
学习目标
1.经历从实际问题抽象出反比例函数的探索过程,发展学生的抽象思维能力。
2.理解反比例函数的概念,会列出实际问题的反比例函数关系式。
自主学习
自学课本54—55页内容。
1、体育课上,同学们跑800米时,每个同学跑步的平均速度v(单位:m/分)随着此同学跑完全程的时间t(单位:h分)的变化而变化,用含t的式子表示v.
2、一次数学课上,老师要同学们画一个面积为10平方厘米的矩形,同学们画后发现矩形相邻两边y(单位:厘米)随着x(单位:厘米)的变化而变化,用含x的式子表示y.
3、已知北京市的总面积为16800平方千米,人均占有土地面积s(单位:平方千米/人)随着全市总人口n(单位:人)的变化而变化,用含n的式子表示s.
以上三个问题的函数解析式为:
1、v=
2、y=
3、s=
小结:判断解析式是不是反比例函数,
看式子是否可以写成
的结构
思考:如何求反比例的解析式呢?
小结2:求反比例函数的解析式只需要找到一个点带入解析式就可以求出k值
小结:
一般地,如果两个变量x,y之间的关系可以表示
成:
(K为常数,且K不为0)的形式,那么
称y是x的反比例函数.
注意:
1.常数
2.自变量x不能为零(因为分母为零时,该分式无意义)
3.当
可以写成
时注意x的指数为
4.注意分母是单项式
亦可表示为xy=k,y=kx-1
反比例函数定义
第一课时
学习目标
1.经历从实际问题抽象出反比例函数的探索过程,发展学生的抽象思维能力。
2.理解反比例函数的概念,会列出实际问题的反比例函数关系式。
自主学习
自学课本54—55页内容。
1、体育课上,同学们跑800米时,每个同学跑步的平均速度v(单位:m/分)随着此同学跑完全程的时间t(单位:h分)的变化而变化,用含t的式子表示v.
2、一次数学课上,老师要同学们画一个面积为10平方厘米的矩形,同学们画后发现矩形相邻两边y(单位:厘米)随着x(单位:厘米)的变化而变化,用含x的式子表示y.
3、已知北京市的总面积为16800平方千米,人均占有土地面积s(单位:平方千米/人)随着全市总人口n(单位:人)的变化而变化,用含n的式子表示s.
以上三个问题的函数解析式为:
1、v=
2、y=
3、s=
小结:判断解析式是不是反比例函数,
看式子是否可以写成
的结构
思考:如何求反比例的解析式呢?
小结2:求反比例函数的解析式只需要找到一个点带入解析式就可以求出k值
小结:
再见
反比例函数定义
第一课时
学习目标
1.经历从实际问题抽象出反比例函数的探索过程,发展学生的抽象思维能力。
2.理解反比例函数的概念,会列出实际问题的反比例函数关系式。
自主学习
自学课本54—55页内容。
1、体育课上,同学们跑800米时,每个同学跑步的平均速度v(单位:m/分)随着此同学跑完全程的时间t(单位:h分)的变化而变化,用含t的式子表示v.
2、一次数学课上,老师要同学们画一个面积为10平方厘米的矩形,同学们画后发现矩形相邻两边y(单位:厘米)随着x(单位:厘米)的变化而变化,用含x的式子表示y.
3、已知北京市的总面积为16800平方千米,人均占有土地面积s(单位:平方千米/人)随着全市总人口n(单位:人)的变化而变化,用含n的式子表示s.
以上三个问题的函数解析式为:
1、v=
2、y=
3、s=
小结:判断解析式是不是反比例函数,
看式子是否可以写成
的结构
思考:如何求反比例的解析式呢?
小结2:求反比例函数的解析式只需要找到一个点带入解析式就可以求出k值
小结:
再见
探究思考:
反比例函数定义
第一课时
学习目标
1.经历从实际问题抽象出反比例函数的探索过程,发展学生的抽象思维能力。
2.理解反比例函数的概念,会列出实际问题的反比例函数关系式。
自主学习
自学课本54—55页内容。
1、体育课上,同学们跑800米时,每个同学跑步的平均速度v(单位:m/分)随着此同学跑完全程的时间t(单位:h分)的变化而变化,用含t的式子表示v.
2、一次数学课上,老师要同学们画一个面积为10平方厘米的矩形,同学们画后发现矩形相邻两边y(单位:厘米)随着x(单位:厘米)的变化而变化,用含x的式子表示y.
3、已知北京市的总面积为16800平方千米,人均占有土地面积s(单位:平方千米/人)随着全市总人口n(单位:人)的变化而变化,用含n的式子表示s.
以上三个问题的函数解析式为:
1、v=
2、y=
3、s=
小结:判断解析式是不是反比例函数,
看式子是否可以写成
的形式
思考:如何求反比例的解析式呢?
小结2:求反比例函数的解析式只需要找到一个点带入解析式就可以求出k值
小结:
再见
探究思考:
随堂练习:挑战自我
1.在下列函数表达式中,x均为自变量,哪些是反比例函数?每一个反比例函数相应的k值是多少?
(b为常数)
1.已知函数y=3xm-7是正比例数,m=
,
2.
.已知函数y=3xm-7是反比例函数,则
m=
.
3、已知y=(m+2)x|m|-3是反比例函数,则m=____
4、反比例函数经过(-2,3),则反比例函数的解析式为_____,
5、反比例函数,当x=2.5时,y=4,则反比例函数的解析式为_____.
6、已知y
是2x-3
成反比例,当x=
时,y=-2,写出y与x的函数关系式
第一课时
学习目标
1.经历从实际问题抽象出反比例函数的探索过程,发展学生的抽象思维能力。
2.理解反比例函数的概念,会列出实际问题的反比例函数关系式。
自主学习
自学课本54—55页内容。
1、体育课上,同学们跑800米时,每个同学跑步的平均速度v(单位:m/分)随着此同学跑完全程的时间t(单位:h分)的变化而变化,用含t的式子表示v.
2、一次数学课上,老师要同学们画一个面积为10平方厘米的矩形,同学们画后发现矩形相邻两边y(单位:厘米)随着x(单位:厘米)的变化而变化,用含x的式子表示y.
3、已知北京市的总面积为16800平方千米,人均占有土地面积s(单位:平方千米/人)随着全市总人口n(单位:人)的变化而变化,用含n的式子表示s.
以上三个问题的函数解析式为:
1、v=
2、y=
3、s=
小结:判断解析式是不是反比例函数,
看式子是否可以写成
的结构
思考:如何求反比例的解析式呢?
小结2:求反比例函数的解析式只需要找到一个点带入解析式就可以求出k值
小结:
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
函数定义:
一般地,在一个变化过程中,如果有两个变量x和y,
并且对于x的每一个给定的值,
y都有唯一的一个值与其相应,那么我们就说x是自变量,y是x的函数。
y=2x+3
y=10x
y=-4x
一次函数定义
一般地,形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数
当b=0时,即y=kx,是正比例函数
是一种特殊的一次函数.
回顾与思考
探究思考:
4、电流I,电阻R,电压U之间满足U=IR,当U=220
v时,你能用含R的代数式表示I吗?变量I是R的函数吗?
一般地,如果两个变量x,y之间的关系可以表示
成:
(K为常数,且K不为0)的形式,那么
称y是x的反比例函数.
注意:
1.常数
2.自变量x不能为零(因为分母为零时,该分式无意义)
3.当
可以写成
时注意x的指数为
4.注意分母是单项式
亦可表示为xy=k,y=kx-1
反比例函数等价形式:(k
≠0)
y=kx-1
xy=k
y与x成反比例
记住这三种形式,都是反比例
定义应用1:下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?
可以改写成
,所以y是x的反比例函数,比例系数k=1。
不具备
的形式,所以y不是x的反比例函数。
y是x的反比例函数,比例系数k=4。
不具备
的形式,所以y不是x的反比例函数。
可以改写成
所以y是x的
反比例函数,比例系数k=
随堂练习:挑战自我
1.在下列函数表达式中,x均为自变量,哪些是反比例函数?每一个反比例函数相应的k值是多少?
(b为常数)
提高练习1:关系式xy+4=0中y是x的反比例函数吗?若是,比例系数k等于多少?若不是,请说明理由。
xy+4=0可以改写成
比例系数k等于-4
所以y是x的反比例函数
反比例等价形式:(k
≠0)
y=kx-1
xy=k
反比例要点:
1、三种写法形式
2、k不等于0(注:k可以是个分数,在分母上)
2、x的次数为-1
1、已知函数
是正比例函数,则
m
=
___
2、
已知函数
是反比例函数,则
m
=
___
。
2
-3
(例2)知识点应用:次数为-1,k不为0
1.若函数y=2x
是反比例函数,
则n_____;
2.若函数y=(m+3)x
是反比例函数,
则m=_____;
n-1
lml-4
=0
3
尝试练习3:
求反比例的解析式
就是求出
k值为多少
例3:已知y是x的反比例函数,当x=2时,y=6.
(1)写出y与x的函数关系式:
(2)求当x=4时y的值.
已知y是x的反比例函数,当x=2时,y=6.
写出y与x的函数关系式:
求当x=4时y的值.
因为当
x=2
时y=6,所以有
∵y与x的函数关系式为
⑵
把
x=4
代入
得
待定系数法求
尝试练习4
(1).写出这个反比例函数的表达式;
解:∵
y是x的反比例函数,
(2).根据函数表达式完成上表.
2
-4
1
一反比例要点:
1、三种写法形式
2、k不等于0(注:k可以是个分数,在分母上)
3、x的次数为-1
二、求反比例解析式:求反比例函数的解析式只需要找到一个点带入解析式就可以求出k值
1.下列函数中哪些是反比例函数,并指出相应k的值?
①
②
③
④
⑤
⑥
⑦
⑧
(9)
xy
=
5
(10)
y
=
3x-1
y
=
2x2
y
=
2x
3
y
=
x
1
y
=
3x
y
=
3
2x
y
=
1
3x
y
=
x
1
【达标检测】
1.已知函数y=3xm-7是正比例数,m=
,
2.
.已知函数y=3xm-7是反比例函数,则
m=
.
3、已知y=(m+2)x|m|-3是反比例函数,则m=____
4、反比例函数经过(-2,3),则反比例函数的解析式为_____,
5、反比例函数,当x=2.5时,y=4,则反比例函数的解析式为_____.
6、已知y
是2x-3
成反比例,当x=
时,y=-2,写出y与x的函数关系式
反比例函数定义
第一课时
学习目标
1.经历从实际问题抽象出反比例函数的探索过程,发展学生的抽象思维能力。
2.理解反比例函数的概念,会列出实际问题的反比例函数关系式。
自主学习
自学课本54—55页内容。
1、体育课上,同学们跑800米时,每个同学跑步的平均速度v(单位:m/分)随着此同学跑完全程的时间t(单位:h分)的变化而变化,用含t的式子表示v.
2、一次数学课上,老师要同学们画一个面积为10平方厘米的矩形,同学们画后发现矩形相邻两边y(单位:厘米)随着x(单位:厘米)的变化而变化,用含x的式子表示y.
3、已知北京市的总面积为16800平方千米,人均占有土地面积s(单位:平方千米/人)随着全市总人口n(单位:人)的变化而变化,用含n的式子表示s.
以上三个问题的函数解析式为:
1、v=
2、y=
3、s=
小结:判断解析式是不是反比例函数,
看式子是否可以写成
的结构
思考:如何求反比例的解析式呢?
小结2:求反比例函数的解析式只需要找到一个点带入解析式就可以求出k值
小结:
一般地,如果两个变量x,y之间的关系可以表示
成:
(K为常数,且K不为0)的形式,那么
称y是x的反比例函数.
注意:
1.常数
2.自变量x不能为零(因为分母为零时,该分式无意义)
3.当
可以写成
时注意x的指数为
4.注意分母是单项式
亦可表示为xy=k,y=kx-1
反比例函数定义
第一课时
学习目标
1.经历从实际问题抽象出反比例函数的探索过程,发展学生的抽象思维能力。
2.理解反比例函数的概念,会列出实际问题的反比例函数关系式。
自主学习
自学课本54—55页内容。
1、体育课上,同学们跑800米时,每个同学跑步的平均速度v(单位:m/分)随着此同学跑完全程的时间t(单位:h分)的变化而变化,用含t的式子表示v.
2、一次数学课上,老师要同学们画一个面积为10平方厘米的矩形,同学们画后发现矩形相邻两边y(单位:厘米)随着x(单位:厘米)的变化而变化,用含x的式子表示y.
3、已知北京市的总面积为16800平方千米,人均占有土地面积s(单位:平方千米/人)随着全市总人口n(单位:人)的变化而变化,用含n的式子表示s.
以上三个问题的函数解析式为:
1、v=
2、y=
3、s=
小结:判断解析式是不是反比例函数,
看式子是否可以写成
的结构
思考:如何求反比例的解析式呢?
小结2:求反比例函数的解析式只需要找到一个点带入解析式就可以求出k值
小结:
再见
反比例函数定义
第一课时
学习目标
1.经历从实际问题抽象出反比例函数的探索过程,发展学生的抽象思维能力。
2.理解反比例函数的概念,会列出实际问题的反比例函数关系式。
自主学习
自学课本54—55页内容。
1、体育课上,同学们跑800米时,每个同学跑步的平均速度v(单位:m/分)随着此同学跑完全程的时间t(单位:h分)的变化而变化,用含t的式子表示v.
2、一次数学课上,老师要同学们画一个面积为10平方厘米的矩形,同学们画后发现矩形相邻两边y(单位:厘米)随着x(单位:厘米)的变化而变化,用含x的式子表示y.
3、已知北京市的总面积为16800平方千米,人均占有土地面积s(单位:平方千米/人)随着全市总人口n(单位:人)的变化而变化,用含n的式子表示s.
以上三个问题的函数解析式为:
1、v=
2、y=
3、s=
小结:判断解析式是不是反比例函数,
看式子是否可以写成
的结构
思考:如何求反比例的解析式呢?
小结2:求反比例函数的解析式只需要找到一个点带入解析式就可以求出k值
小结:
再见
探究思考:
反比例函数定义
第一课时
学习目标
1.经历从实际问题抽象出反比例函数的探索过程,发展学生的抽象思维能力。
2.理解反比例函数的概念,会列出实际问题的反比例函数关系式。
自主学习
自学课本54—55页内容。
1、体育课上,同学们跑800米时,每个同学跑步的平均速度v(单位:m/分)随着此同学跑完全程的时间t(单位:h分)的变化而变化,用含t的式子表示v.
2、一次数学课上,老师要同学们画一个面积为10平方厘米的矩形,同学们画后发现矩形相邻两边y(单位:厘米)随着x(单位:厘米)的变化而变化,用含x的式子表示y.
3、已知北京市的总面积为16800平方千米,人均占有土地面积s(单位:平方千米/人)随着全市总人口n(单位:人)的变化而变化,用含n的式子表示s.
以上三个问题的函数解析式为:
1、v=
2、y=
3、s=
小结:判断解析式是不是反比例函数,
看式子是否可以写成
的形式
思考:如何求反比例的解析式呢?
小结2:求反比例函数的解析式只需要找到一个点带入解析式就可以求出k值
小结:
再见
探究思考:
随堂练习:挑战自我
1.在下列函数表达式中,x均为自变量,哪些是反比例函数?每一个反比例函数相应的k值是多少?
(b为常数)
1.已知函数y=3xm-7是正比例数,m=
,
2.
.已知函数y=3xm-7是反比例函数,则
m=
.
3、已知y=(m+2)x|m|-3是反比例函数,则m=____
4、反比例函数经过(-2,3),则反比例函数的解析式为_____,
5、反比例函数,当x=2.5时,y=4,则反比例函数的解析式为_____.
6、已知y
是2x-3
成反比例,当x=
时,y=-2,写出y与x的函数关系式
