华东师大版八年级数学下册课件:18.1.1平行四边形的性质(共18张PPT)
文档属性
| 名称 | 华东师大版八年级数学下册课件:18.1.1平行四边形的性质(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 12:48:58 | ||
图片预览





文档简介
义务教育教科书(华东师大版)八年级下册§18.1
平行四边形的性质
1、理解并掌握平行四边形的概念以及
平行四边形对边、对角相等的性质;
2、运用平行四边形的性质进行有关的计算
与证明,进而解决简单的问题;
3、了解两条平行线之间距离的意义,
能度量两条平行线之间的距离.
与目标对话
对照要求 达成目标
与生活对话
问题:下面的图片中,有你熟悉的哪些图形?
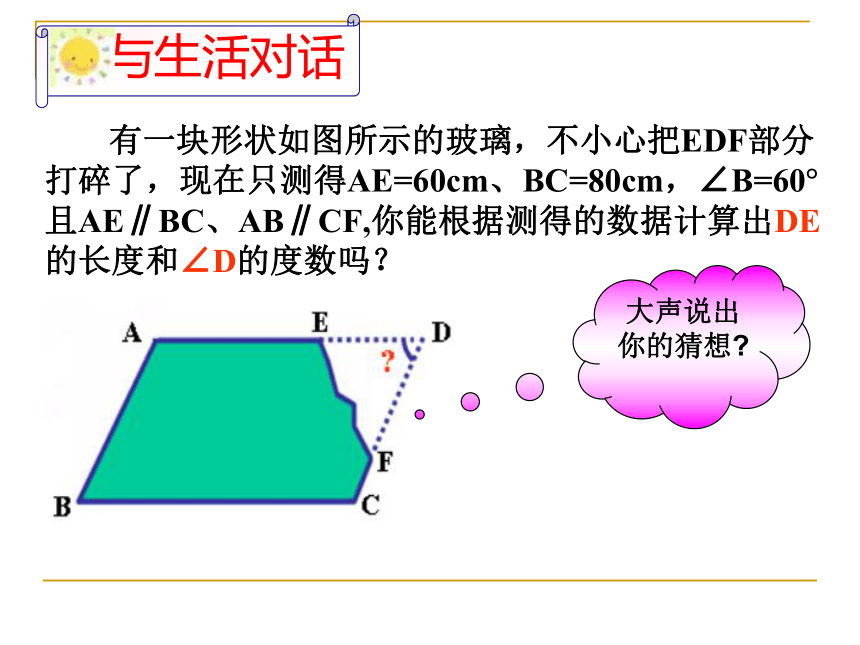
有一块形状如图所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
与生活对话
大声说出
你的猜想?
与文本对话
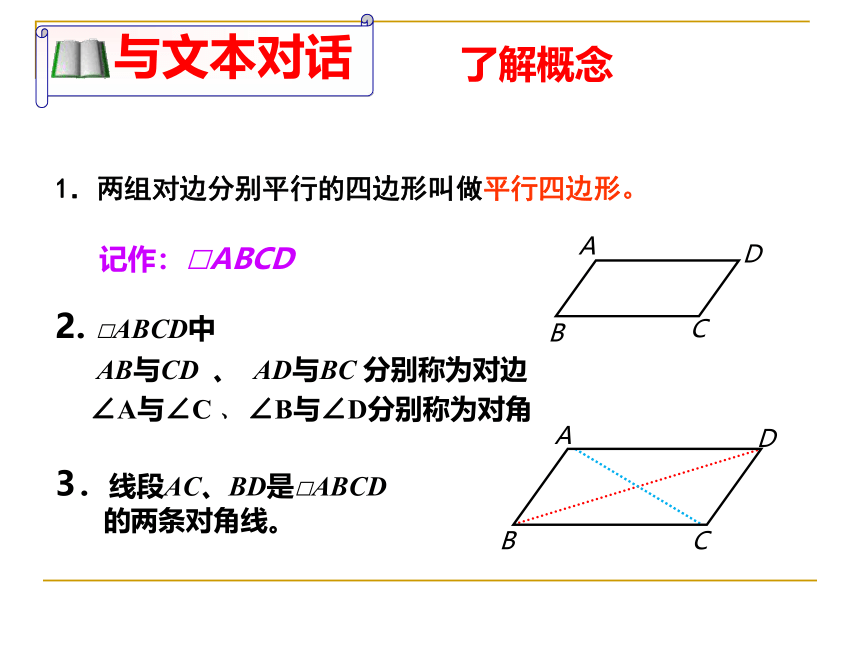
1.两组对边分别平行的四边形叫做平行四边形。
记作:□ABCD
3.线段AC、BD是□ABCD
的两条对角线。
2. □ABCD中
AB与CD 、 AD与BC 分别称为对边
∠A与∠C 、 ∠B与∠D分别称为对角
了解概念
A
D
C
B
A
D
C
B
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
与文本对话
理解定义
与探究对话
画板演示 过程重现
小组合作 发现性质
A
D
B
C
A
D
C
B
1、边的数量关系
2、角的数量关系
与探究对话
已知:如图, □ABCD
求证:AB=CD,AD=CB;∠A=∠C,∠ABC=∠CDA
证明:连结BD
A
B
C
D
即∠ABC=∠CDA
∴AB∥DC,AD∥BC(平行四边形的两组对边分别平行)
∴∠1=∠2,∠3=∠4
又∵ BD=DB
∴ ABD≌ CDB(ASA)
∴AB=CD, AD =CB,∠A=∠C
由∵∠1=∠2和∠3=∠4,得
∠1+∠4=∠2+∠3
∵ 四边形ABCD是平行四边形
1
2
4
3
与题组对话
先学检测 反馈落实
140°
140°
40°
50°
130°
5
8
30
12
18
60°
120°
10
改编训练 提升技能
与改编对话
如图,已知□ABCD中,∠DAB的平分线AE交CD于E,
且AB=8,EC=3,求□ABCD的周长.
拓展知识
与实践对话
A
C
B
D
概括:
①平行线的又一个性质: ;
②两条平行线之间的距离的意义: .
平行线之间的距离处处相等
两条直线平行,其中一条直线上的任一点到另一条直线的距离,
拓展知识 灵活应用
与实践对话
与收获对话
承前启后 升华知识
有一块形状如图所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解释问题
升华知识
用两个三边不等的完全相同的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常连结对角线,转化为两个全等三角形来解题。
与探究对话
课外作业与综合实践
与实践对话
与改编对话
编制问题 提升能力
如图是某区部分街道示意图,其中: AD // EG // BC ,
AB // FH // DC,试问.
(2)从B站乘车到D站有两条
可直接到达的公交车路线,
路线1:B—E—A—F—D,
路线2:B—H—O—G—D,
请比较两条路线路程的长短,
并说明理由。
A
C
D
F
H
O
B
(1)图中的平行四边形共有_____个.
E
G
平行四边形的性质
1、理解并掌握平行四边形的概念以及
平行四边形对边、对角相等的性质;
2、运用平行四边形的性质进行有关的计算
与证明,进而解决简单的问题;
3、了解两条平行线之间距离的意义,
能度量两条平行线之间的距离.
与目标对话
对照要求 达成目标
与生活对话
问题:下面的图片中,有你熟悉的哪些图形?
有一块形状如图所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
与生活对话
大声说出
你的猜想?
与文本对话
1.两组对边分别平行的四边形叫做平行四边形。
记作:□ABCD
3.线段AC、BD是□ABCD
的两条对角线。
2. □ABCD中
AB与CD 、 AD与BC 分别称为对边
∠A与∠C 、 ∠B与∠D分别称为对角
了解概念
A
D
C
B
A
D
C
B
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
与文本对话
理解定义
与探究对话
画板演示 过程重现
小组合作 发现性质
A
D
B
C
A
D
C
B
1、边的数量关系
2、角的数量关系
与探究对话
已知:如图, □ABCD
求证:AB=CD,AD=CB;∠A=∠C,∠ABC=∠CDA
证明:连结BD
A
B
C
D
即∠ABC=∠CDA
∴AB∥DC,AD∥BC(平行四边形的两组对边分别平行)
∴∠1=∠2,∠3=∠4
又∵ BD=DB
∴ ABD≌ CDB(ASA)
∴AB=CD, AD =CB,∠A=∠C
由∵∠1=∠2和∠3=∠4,得
∠1+∠4=∠2+∠3
∵ 四边形ABCD是平行四边形
1
2
4
3
与题组对话
先学检测 反馈落实
140°
140°
40°
50°
130°
5
8
30
12
18
60°
120°
10
改编训练 提升技能
与改编对话
如图,已知□ABCD中,∠DAB的平分线AE交CD于E,
且AB=8,EC=3,求□ABCD的周长.
拓展知识
与实践对话
A
C
B
D
概括:
①平行线的又一个性质: ;
②两条平行线之间的距离的意义: .
平行线之间的距离处处相等
两条直线平行,其中一条直线上的任一点到另一条直线的距离,
拓展知识 灵活应用
与实践对话
与收获对话
承前启后 升华知识
有一块形状如图所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解释问题
升华知识
用两个三边不等的完全相同的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常连结对角线,转化为两个全等三角形来解题。
与探究对话
课外作业与综合实践
与实践对话
与改编对话
编制问题 提升能力
如图是某区部分街道示意图,其中: AD // EG // BC ,
AB // FH // DC,试问.
(2)从B站乘车到D站有两条
可直接到达的公交车路线,
路线1:B—E—A—F—D,
路线2:B—H—O—G—D,
请比较两条路线路程的长短,
并说明理由。
A
C
D
F
H
O
B
(1)图中的平行四边形共有_____个.
E
G
