华东师大版八年级数学下册课件:18.2.1平行四边形的判定 (共15张PPT)
文档属性
| 名称 | 华东师大版八年级数学下册课件:18.2.1平行四边形的判定 (共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 453.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 12:49:35 | ||
图片预览




文档简介
18.2.1
平行四边形的判定
边
平行四边形的对边分别平行
平行四边形的对边分别相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边行
∴
AB∥CD,AD∥BC
。
AB=CD,AD=BC
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴
∠
A=∠
C,
∠
D=∠
B
∠
A+∠
B=
,
∠
A+∠
D=
…
∵四边形ABCD是平行边形
∴OA=OC,OB=OD
通过前面的学习,我们知道,平行四边形对边相等、对角相等、对角线互相平分。那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?
创设情境,引入新课
a.平行四边形两组对边分别平行.
b.平行四边形两组对边分别相等.
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
(定义)
可以判定一个四边形是平行四边形
你能分别说出他们的逆命题吗?
这些逆命题成立吗?
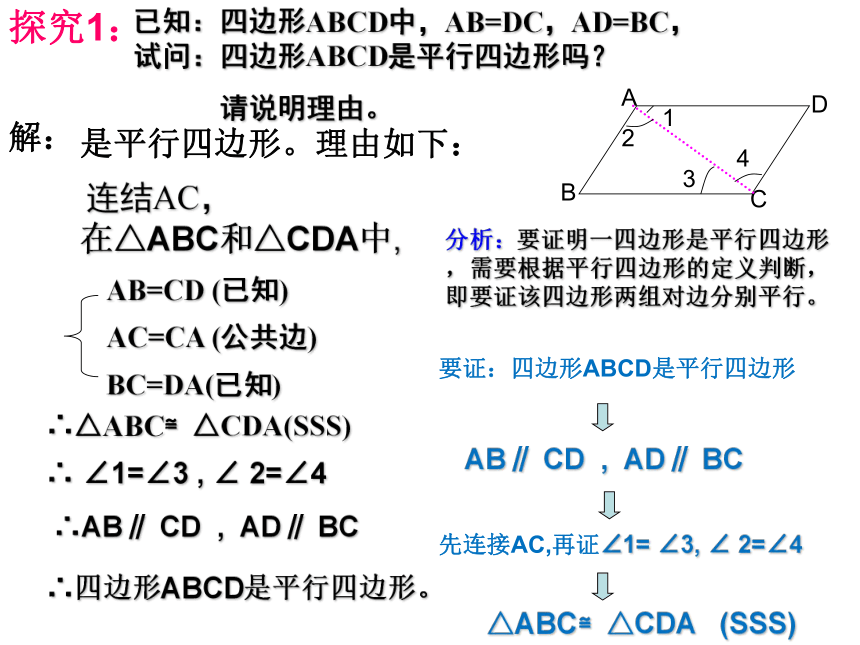
探究1:
已知:四边形ABCD中,AB=DC,AD=BC,试问:四边形ABCD是平行四边形吗?
请说明理由。
分析:要证明一四边形是平行四边形,需要根据平行四边形的定义判断,即要证该四边形两组对边分别平行。
要证:四边形ABCD是平行四边形
AB∥
CD
,
AD∥
BC
先连接AC,再证∠1=
∠3,
∠
2=∠4
△ABC≌△CDA
(SSS)
解:
是平行四边形。理由如下:
连结AC,
AB=CD
(已知)
AC=CA
(公共边)
BC=DA(已知)
∴△ABC≌△CDA(SSS)
在△ABC和△CDA中,
∴
∠1=∠3
,
∠
2=∠4
∴AB∥
CD
,
AD∥
BC
∴四边形ABCD是平行四边形。
A
B
C
D
1
2
3
4
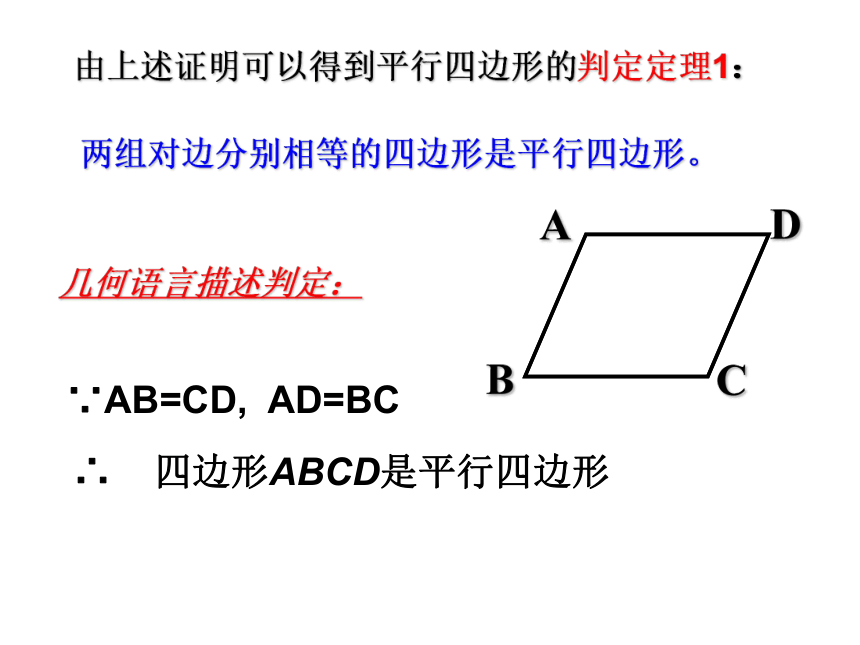
由上述证明可以得到平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
几何语言描述判定:
A
B
C
D
A
B
C
D
∵AB=CD,
AD=BC
∴
四边形ABCD是平行四边形
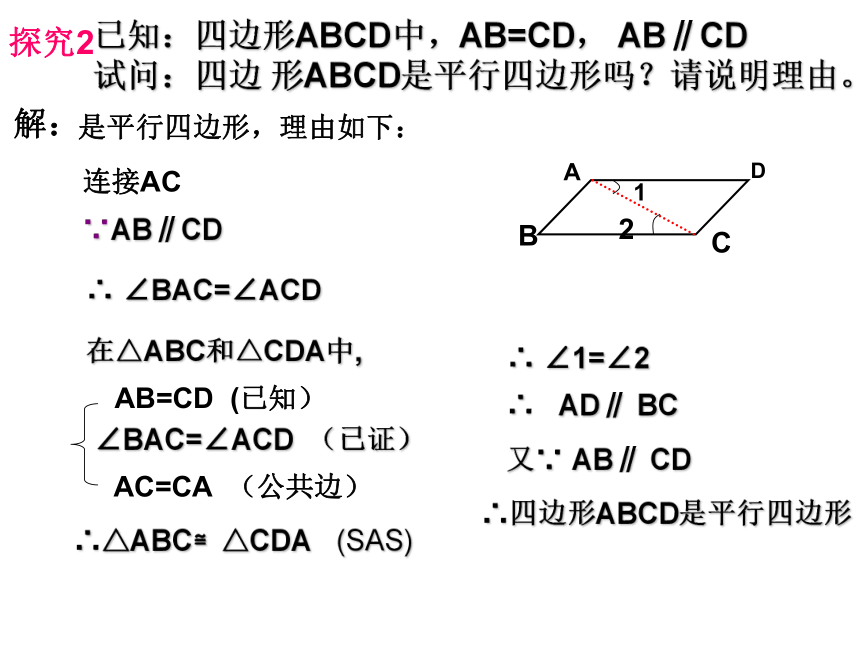
探究2
已知:四边形ABCD中,AB=CD,
AB∥CD
试问:四边
形ABCD是平行四边形吗?请说明理由。
B
解:
连接AC
A
C
D
1
2
是平行四边形,理由如下:
∵AB∥CD
∴
∠BAC=∠ACD
在△ABC和△CDA中,
AB=CD
(已知)
∠BAC=∠ACD
(已证)
AC=CA
(公共边)
∴△ABC≌△CDA
(SAS)
∴
∠1=∠2
∴
AD∥
BC
又∵
AB∥
CD
∴四边形ABCD是平行四边形
由上述证明可以得到平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形。
几何语言描述判定:
A
B
C
D
AD
BC
“
”
读作“平行且相等”.
∵
∴
四边形ABCD是平行四边形
(1)若AB∥CD,补充条件_____,
使四边形ABCD为平行四边形。
(2)若AD=CB,补充条件_____,使四边形ABCD为平行四边形。
AD∥CB
或者AB=CD
AD∥CB
或者AB=CD
练一练
1填空:
C
B
D
A
3、填空题:
如图,在四边形ABCD中,
A
B
C
D
①如果AD=8cm,AB=4cm,且BC=____cm,CD=____cm,那么四边形ABCD是平行四边形。
②如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形。
8
4
点评:两组对边相等的四边形是平行四边形
6
点评:一组对边平行且相等的四边形是平行四边形
2、在下列条件中,不能判定四边形是平行四边形的是(
)
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D)
AB∥CD,AD=BC
D
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
(一组对边平行且相等)
A
B
D
C
一组对边平行,另一组对边相等的四边形是平行四边形
判断真假命题:
C
B
D
A
C
B
D
A
是假命题
例:
如图,在平行四边形ABCD中,E、F分别是边BC和AD上的两点,且BF=DE。
求证:四边形DEBF为平行四边形
你还有其他方法吗?
应用
变式.已知:如图,E,F分别是
的边AD,BC的中点。
求证:BE=DF.
D
F
E
C
B
A
证明:
归纳小结
定义:两组对边分别平行的四边形是平行四边形。
判定定理1
两组对边分别相等的四边形是平行四边形。
判定定理2
一组对边平行且相等的四边形是平行四边形。
本节
课主要学行四边形的判定定理:
平行四边形的判定
边
平行四边形的对边分别平行
平行四边形的对边分别相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边行
∴
AB∥CD,AD∥BC
。
AB=CD,AD=BC
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴
∠
A=∠
C,
∠
D=∠
B
∠
A+∠
B=
,
∠
A+∠
D=
…
∵四边形ABCD是平行边形
∴OA=OC,OB=OD
通过前面的学习,我们知道,平行四边形对边相等、对角相等、对角线互相平分。那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?
创设情境,引入新课
a.平行四边形两组对边分别平行.
b.平行四边形两组对边分别相等.
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
(定义)
可以判定一个四边形是平行四边形
你能分别说出他们的逆命题吗?
这些逆命题成立吗?
探究1:
已知:四边形ABCD中,AB=DC,AD=BC,试问:四边形ABCD是平行四边形吗?
请说明理由。
分析:要证明一四边形是平行四边形,需要根据平行四边形的定义判断,即要证该四边形两组对边分别平行。
要证:四边形ABCD是平行四边形
AB∥
CD
,
AD∥
BC
先连接AC,再证∠1=
∠3,
∠
2=∠4
△ABC≌△CDA
(SSS)
解:
是平行四边形。理由如下:
连结AC,
AB=CD
(已知)
AC=CA
(公共边)
BC=DA(已知)
∴△ABC≌△CDA(SSS)
在△ABC和△CDA中,
∴
∠1=∠3
,
∠
2=∠4
∴AB∥
CD
,
AD∥
BC
∴四边形ABCD是平行四边形。
A
B
C
D
1
2
3
4
由上述证明可以得到平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
几何语言描述判定:
A
B
C
D
A
B
C
D
∵AB=CD,
AD=BC
∴
四边形ABCD是平行四边形
探究2
已知:四边形ABCD中,AB=CD,
AB∥CD
试问:四边
形ABCD是平行四边形吗?请说明理由。
B
解:
连接AC
A
C
D
1
2
是平行四边形,理由如下:
∵AB∥CD
∴
∠BAC=∠ACD
在△ABC和△CDA中,
AB=CD
(已知)
∠BAC=∠ACD
(已证)
AC=CA
(公共边)
∴△ABC≌△CDA
(SAS)
∴
∠1=∠2
∴
AD∥
BC
又∵
AB∥
CD
∴四边形ABCD是平行四边形
由上述证明可以得到平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形。
几何语言描述判定:
A
B
C
D
AD
BC
“
”
读作“平行且相等”.
∵
∴
四边形ABCD是平行四边形
(1)若AB∥CD,补充条件_____,
使四边形ABCD为平行四边形。
(2)若AD=CB,补充条件_____,使四边形ABCD为平行四边形。
AD∥CB
或者AB=CD
AD∥CB
或者AB=CD
练一练
1填空:
C
B
D
A
3、填空题:
如图,在四边形ABCD中,
A
B
C
D
①如果AD=8cm,AB=4cm,且BC=____cm,CD=____cm,那么四边形ABCD是平行四边形。
②如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形。
8
4
点评:两组对边相等的四边形是平行四边形
6
点评:一组对边平行且相等的四边形是平行四边形
2、在下列条件中,不能判定四边形是平行四边形的是(
)
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D)
AB∥CD,AD=BC
D
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
(一组对边平行且相等)
A
B
D
C
一组对边平行,另一组对边相等的四边形是平行四边形
判断真假命题:
C
B
D
A
C
B
D
A
是假命题
例:
如图,在平行四边形ABCD中,E、F分别是边BC和AD上的两点,且BF=DE。
求证:四边形DEBF为平行四边形
你还有其他方法吗?
应用
变式.已知:如图,E,F分别是
的边AD,BC的中点。
求证:BE=DF.
D
F
E
C
B
A
证明:
归纳小结
定义:两组对边分别平行的四边形是平行四边形。
判定定理1
两组对边分别相等的四边形是平行四边形。
判定定理2
一组对边平行且相等的四边形是平行四边形。
本节
课主要学行四边形的判定定理:
