华东师大版八年级下册17.2.1平面直角坐标系课件 (共18张PPT)
文档属性
| 名称 | 华东师大版八年级下册17.2.1平面直角坐标系课件 (共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 13:21:21 | ||
图片预览






文档简介
17.2.1平面直角坐标系
什么是数轴?
在直线上规定了原点、正方向、单位长度就构成了数轴。
·
0
1
2
3
4
-3
-2
-1
原点
复习回顾
思考:数轴上的点与实数间有什么关系呢 ?
数轴上的点与实数是一一对应的.
找自己的座位
怎样确定北京在中国地图上的位置?
阅读教材,思考:
(1)如何建立平面直角坐标系?
(2)指出坐标系中各部分的名称
(x轴,y轴,原点及第一、二、三、四象限)
新课推进
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
平面直角坐标系
两条数轴:
(1)原点重合
(2)互相垂直
(3)相同单位长度
·
B
·
A
(-4,1)
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
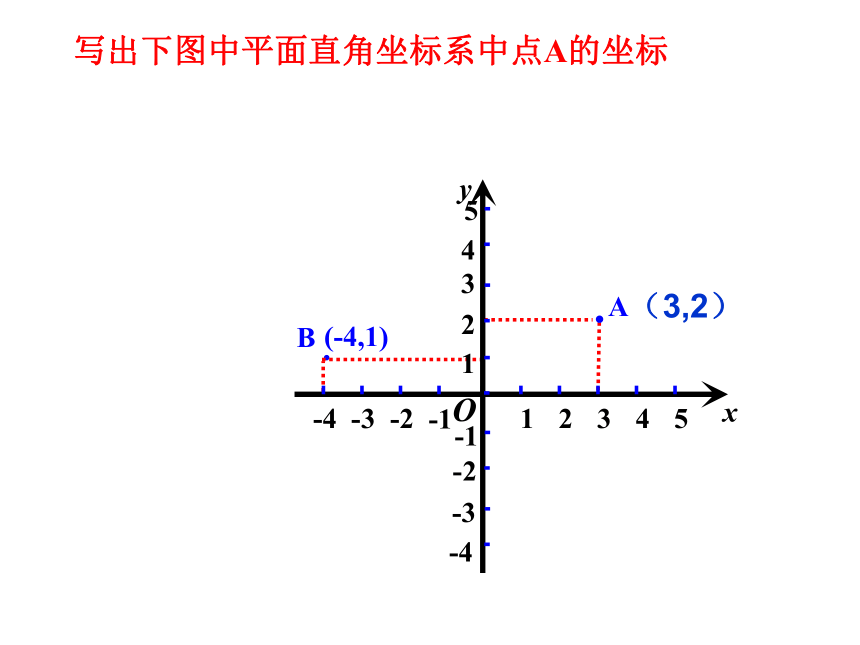
写出下图中平面直角坐标系中点A的坐标
(3,2)
·
M(-2,2)
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
在平面直角坐标系中描出点M(-2,2)
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
在平面直角坐标系中描出点P(3,2)、Q(2,3)、
S(-2,3)、R(3,-2),点Q(2,3)与点P(3,2)是同一个点吗?S(-2,3)与R(3,-2)是同一个点吗?
Q(2,3)
S(-2,3)
R(3,-2)
P(3,2)
·
·
·
·
试一试
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
写出图中点 A、B、C、D、E、F 的坐标,观察你所写出的这些点的坐标,思考:
(1)在四个象限内的点的坐标各有什么特征?
(2)两条坐标轴上的点的坐标各有什么特征?
D
·
·F
·
·
·
·E
A
(-1,2)
B
C
(0, 3)
(-2, 0)
试一试
(-1,-1)
(2,1)
(2,-1)
思考:平面直角坐标系中的点和有序实数对有什么关系?
平面直角坐标系内的点 有序实数对
一一对应
4.若点A(a,3)在第一象限,
则点B(-a,-3)在第 象限
5.若点A(a-2,5)在第二象限,则a的取值范围是
.
1. 已知点P( -3 , 2 ),则点P位置在第______象限.
2. 已知点Q(0,-3),说出点Q的位置在_______.
3.若点 P(x,y)在第四象限,| x |=5,| y |=4,则 P 点的坐标为 .
二
y轴上
(5,-4)
三
a<2
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
A(2,4)
B(2,-4)
D(-2,-4)
·
·
·
·
C(-2,4)
在直角坐标系中描出点A(2,4),分别找出它关于x轴,y轴及原点的对称点,并写出这些点的坐标.
探究:对称点的坐标特点
6.已知点P(3,-4),
P点关于x轴的对称点P1的坐标是 ;
P点关于y轴的对称点P2的坐标是 ;
P点关于原点的对称点P3的坐标是 。
7.已知点P(a,b),
P点关于x轴的对称点P1的坐标是 ;
P点关于y轴的对称点P2的坐标是 ;
P点关于原点的对称点P3的坐标是
(3,4)
(-3,-4)
(-3,4)
(-a,-b)
(-a,b)
(a,-b)
8.点(3,5)与点(3,-5)关于________轴对称.
X
9.点A关于原点对称点的坐标为(2,3),
则点A 关于 y 轴对称点的坐标为 .
(2,-3)
10.若点(m,2)与(3,n)关于原点对称,则m+n的值是 。
-5
笛卡儿是著名的法国数学家,他用平面上的一点到两条固定直线的距离来确定点的距离,用坐标来描述平面和空间上的点,他进而创立了解析几何学,表明了几何问题不仅可以归结成为代数形式,而且可以通过代数变换来发现几何性质,证明几何性质。
代数 几何
坐 标
知识上:
1.平面直角坐标系的有关概念及画法;
2.在直角坐标系中,根据坐标找出点;由点求出坐标的方法;
3.在四个象限内的点的坐标特征;
两条坐标轴上的点的坐标特征;
4.分别关于x轴、y轴及原点的对称的两点坐标之间的关系
5.平面直角坐标系内的点 有序实数对。
一一对应
课堂小结
思想方法:数形结合思想,对应思想
什么是数轴?
在直线上规定了原点、正方向、单位长度就构成了数轴。
·
0
1
2
3
4
-3
-2
-1
原点
复习回顾
思考:数轴上的点与实数间有什么关系呢 ?
数轴上的点与实数是一一对应的.
找自己的座位
怎样确定北京在中国地图上的位置?
阅读教材,思考:
(1)如何建立平面直角坐标系?
(2)指出坐标系中各部分的名称
(x轴,y轴,原点及第一、二、三、四象限)
新课推进
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
平面直角坐标系
两条数轴:
(1)原点重合
(2)互相垂直
(3)相同单位长度
·
B
·
A
(-4,1)
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
写出下图中平面直角坐标系中点A的坐标
(3,2)
·
M(-2,2)
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
在平面直角坐标系中描出点M(-2,2)
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
在平面直角坐标系中描出点P(3,2)、Q(2,3)、
S(-2,3)、R(3,-2),点Q(2,3)与点P(3,2)是同一个点吗?S(-2,3)与R(3,-2)是同一个点吗?
Q(2,3)
S(-2,3)
R(3,-2)
P(3,2)
·
·
·
·
试一试
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
写出图中点 A、B、C、D、E、F 的坐标,观察你所写出的这些点的坐标,思考:
(1)在四个象限内的点的坐标各有什么特征?
(2)两条坐标轴上的点的坐标各有什么特征?
D
·
·F
·
·
·
·E
A
(-1,2)
B
C
(0, 3)
(-2, 0)
试一试
(-1,-1)
(2,1)
(2,-1)
思考:平面直角坐标系中的点和有序实数对有什么关系?
平面直角坐标系内的点 有序实数对
一一对应
4.若点A(a,3)在第一象限,
则点B(-a,-3)在第 象限
5.若点A(a-2,5)在第二象限,则a的取值范围是
.
1. 已知点P( -3 , 2 ),则点P位置在第______象限.
2. 已知点Q(0,-3),说出点Q的位置在_______.
3.若点 P(x,y)在第四象限,| x |=5,| y |=4,则 P 点的坐标为 .
二
y轴上
(5,-4)
三
a<2
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
0
-3
x
A(2,4)
B(2,-4)
D(-2,-4)
·
·
·
·
C(-2,4)
在直角坐标系中描出点A(2,4),分别找出它关于x轴,y轴及原点的对称点,并写出这些点的坐标.
探究:对称点的坐标特点
6.已知点P(3,-4),
P点关于x轴的对称点P1的坐标是 ;
P点关于y轴的对称点P2的坐标是 ;
P点关于原点的对称点P3的坐标是 。
7.已知点P(a,b),
P点关于x轴的对称点P1的坐标是 ;
P点关于y轴的对称点P2的坐标是 ;
P点关于原点的对称点P3的坐标是
(3,4)
(-3,-4)
(-3,4)
(-a,-b)
(-a,b)
(a,-b)
8.点(3,5)与点(3,-5)关于________轴对称.
X
9.点A关于原点对称点的坐标为(2,3),
则点A 关于 y 轴对称点的坐标为 .
(2,-3)
10.若点(m,2)与(3,n)关于原点对称,则m+n的值是 。
-5
笛卡儿是著名的法国数学家,他用平面上的一点到两条固定直线的距离来确定点的距离,用坐标来描述平面和空间上的点,他进而创立了解析几何学,表明了几何问题不仅可以归结成为代数形式,而且可以通过代数变换来发现几何性质,证明几何性质。
代数 几何
坐 标
知识上:
1.平面直角坐标系的有关概念及画法;
2.在直角坐标系中,根据坐标找出点;由点求出坐标的方法;
3.在四个象限内的点的坐标特征;
两条坐标轴上的点的坐标特征;
4.分别关于x轴、y轴及原点的对称的两点坐标之间的关系
5.平面直角坐标系内的点 有序实数对。
一一对应
课堂小结
思想方法:数形结合思想,对应思想
