华东师大版八年级下册18.1.3平行四边形对角线的性质课件 (共18张PPT)
文档属性
| 名称 | 华东师大版八年级下册18.1.3平行四边形对角线的性质课件 (共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 21:11:39 | ||
图片预览



文档简介
18.1 平行四边形
3.平行四边形对角线的性质
数学八年级上册(华师大版)
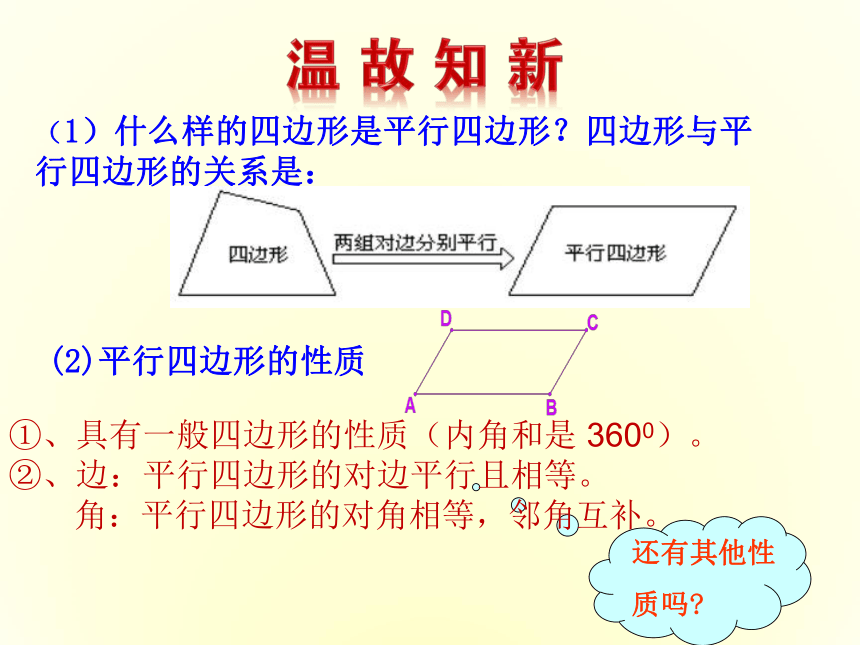
(2)平行四边形的性质
还有其他性
质吗?
(1)什么样的四边形是平行四边形?四边形与平行四边形的关系是:
①、具有一般四边形的性质(内角和是 3600)。
②、边:平行四边形的对边平行且相等。
角:平行四边形的对角相等,邻角互补。
A
B
D
C
O
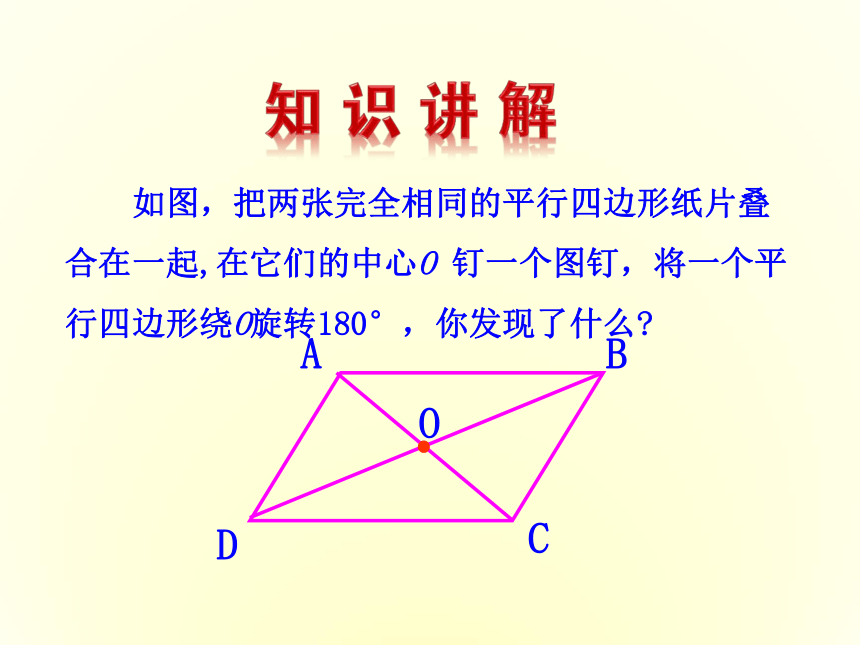
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
结论
你能证明 它吗?
平行四边形的对角线互相平分.
ABCD绕它的中心O旋转180°后与自身重合,这时我们说 ABCD是中心对称图形,点O叫对称中心.
已知:如图: ABCD的对角线AC和BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
平行四边形的对角线互相平分.
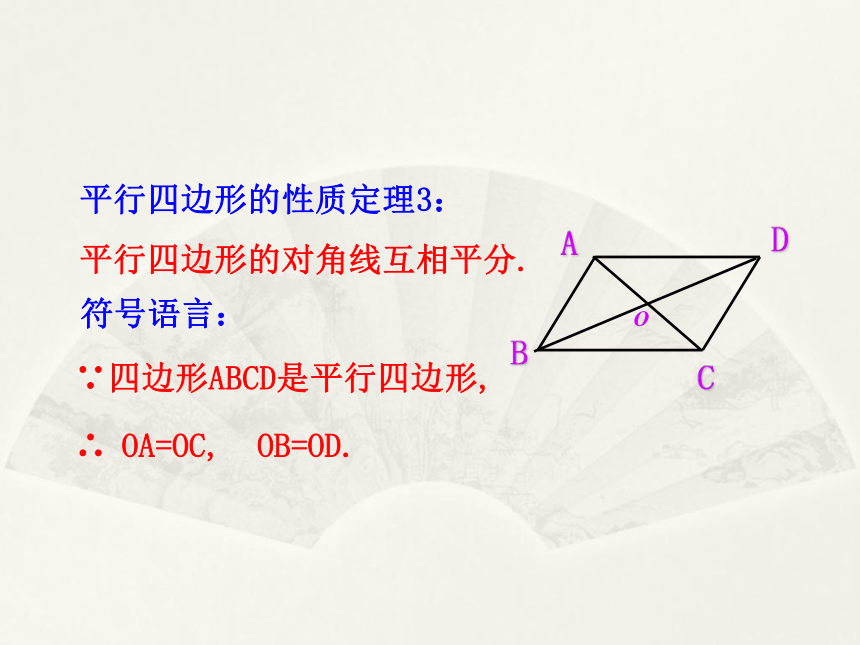
平行四边形的性质定理3:
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形,
OA=OC,
OB=OD.
∴
A
D
B
C
O
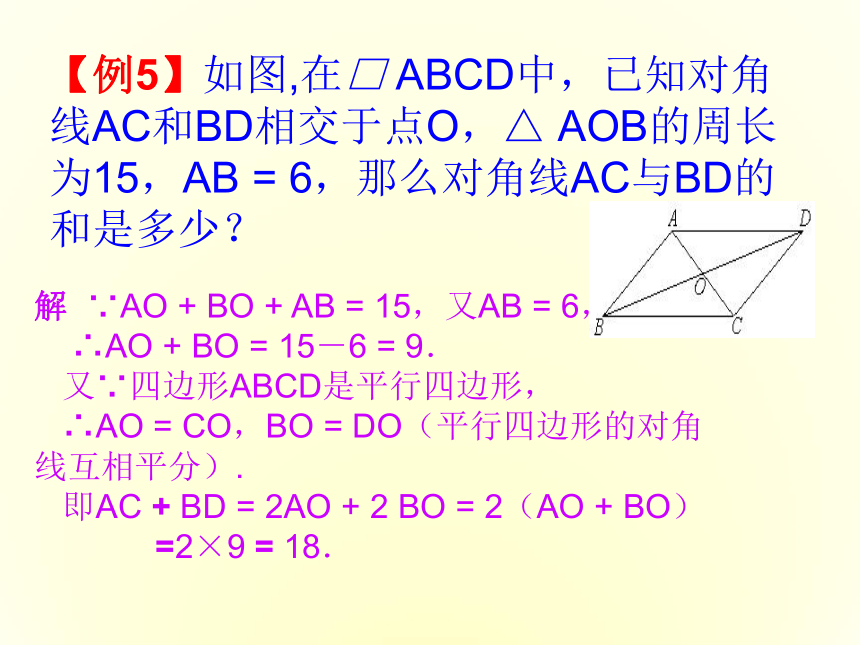
解? ∵AO + BO + AB = 15,又AB = 6,
∴AO + BO = 15-6 = 9.
又∵四边形ABCD是平行四边形,
∴AO = CO,BO = DO(平行四边形的对角线互相平分).
即AC + BD = 2AO + 2 BO = 2(AO + BO)
=2×9 = 18.
【例5】如图,在□ ABCD中,已知对角线AC和BD相交于点O,△?AOB的周长为15,AB = 6,那么对角线AC与BD的和是多少?
例6: 如图,□ABCD的对角线AC,BD交于点O, EF过点O且与边AD、BC分别交于点E、F.求证:OE=OF.
证明: ∵ 四边形ABCD是平行四边形
∴OA=OC
又∵AD∥BC,
∴∠EAO=∠FCO.
又∵∠AOE=∠COF,
∴ΔAEO≌ ΔCFO.
∴OE=OF
思考 改变直线EF的位置,OE=OF还成立吗?
1.平行四边形具有而一般四边形不具有的特征是( )
A.不稳定性 B.对角线互相平分
C.内角和为360度 D.外角和为360度
B
【跟踪训练】
2.若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
D
O
D
B
A
C
3.如图,在□ABCD中, 对角线AC,BD相交于点O,且AC+BD=20, △AOB的周长等于15,则CD=______.
5
4.如图,在□ ABCD中,对角线AC,BD交于点O,AC=10,
BD=8,则AD的取值范围是 __.
O
D
B
A
C
●
1<AD<9
1.(邵阳·中考)如图所示,在□ ABCD中,对角线AC,BD相交于点O,且AB≠AD,则下列式子不正确的
是( )
A.AC⊥BD B.AB=CD
C.BO=OD D.∠BAD=∠BCD
A
D
C
O
B
【解析】选A.由题意知□ABCD是一般的平行四边形,对角线不一定垂直.
2.已知EF过□ ABCD的对角线的交点O,交AD于点E,交BC于点F,已知AB=4,BC=5,OE=1.5,那么四边形EFCD的周长是( )
A.14 B.12 C.16 D.8
【解析】选B.由平行四边形的性质易证,AB=CD=4,BC=AD=5,
△AEO≌△CFO,所以OE=OF=1.5,AE=CF, 所以四边形EFCD的周长为:CD+DE+EF+FC=CD+BC+EF=4+5+3=12.
3.如图,□ ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )
A.3 B.6
C.12 D.24
【解析】选C.观察图形会发现,每一小块阴影三角形都
与它相对的三角形全等,则阴影部分的面积等于平行四
边形面积的一半.故S阴影= = ×6×4=12.
4.如图,□ ABCD中,AE⊥BD,∠EAD=60°,AE=2 cm,AC+BD=14 cm,则△OBC的周长是____cm.
【解析】在□ABCD中,BC=AD,OA=OC,OB=OD,
∵AE⊥BD,∠EAD=60°,AE=2 cm,∴AD=4 cm,BC=4cm,
∵AC+BD=14 cm,
∴OB+OC=7 cm,
∴△OBC的周长=OB+OC+BC=11 cm.
答案:11
通过本课时的学习,需要我们
1.知道平行四边形中心对称的特征.
2.掌握平行四边形对角线互相平分的性质并能利用这一性质进行计算或证明.
3.综合运用平行四边形的性质进行计算或证明.
3.平行四边形对角线的性质
数学八年级上册(华师大版)
(2)平行四边形的性质
还有其他性
质吗?
(1)什么样的四边形是平行四边形?四边形与平行四边形的关系是:
①、具有一般四边形的性质(内角和是 3600)。
②、边:平行四边形的对边平行且相等。
角:平行四边形的对角相等,邻角互补。
A
B
D
C
O
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
结论
你能证明 它吗?
平行四边形的对角线互相平分.
ABCD绕它的中心O旋转180°后与自身重合,这时我们说 ABCD是中心对称图形,点O叫对称中心.
已知:如图: ABCD的对角线AC和BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
平行四边形的对角线互相平分.
平行四边形的性质定理3:
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形,
OA=OC,
OB=OD.
∴
A
D
B
C
O
解? ∵AO + BO + AB = 15,又AB = 6,
∴AO + BO = 15-6 = 9.
又∵四边形ABCD是平行四边形,
∴AO = CO,BO = DO(平行四边形的对角线互相平分).
即AC + BD = 2AO + 2 BO = 2(AO + BO)
=2×9 = 18.
【例5】如图,在□ ABCD中,已知对角线AC和BD相交于点O,△?AOB的周长为15,AB = 6,那么对角线AC与BD的和是多少?
例6: 如图,□ABCD的对角线AC,BD交于点O, EF过点O且与边AD、BC分别交于点E、F.求证:OE=OF.
证明: ∵ 四边形ABCD是平行四边形
∴OA=OC
又∵AD∥BC,
∴∠EAO=∠FCO.
又∵∠AOE=∠COF,
∴ΔAEO≌ ΔCFO.
∴OE=OF
思考 改变直线EF的位置,OE=OF还成立吗?
1.平行四边形具有而一般四边形不具有的特征是( )
A.不稳定性 B.对角线互相平分
C.内角和为360度 D.外角和为360度
B
【跟踪训练】
2.若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
D
O
D
B
A
C
3.如图,在□ABCD中, 对角线AC,BD相交于点O,且AC+BD=20, △AOB的周长等于15,则CD=______.
5
4.如图,在□ ABCD中,对角线AC,BD交于点O,AC=10,
BD=8,则AD的取值范围是 __.
O
D
B
A
C
●
1<AD<9
1.(邵阳·中考)如图所示,在□ ABCD中,对角线AC,BD相交于点O,且AB≠AD,则下列式子不正确的
是( )
A.AC⊥BD B.AB=CD
C.BO=OD D.∠BAD=∠BCD
A
D
C
O
B
【解析】选A.由题意知□ABCD是一般的平行四边形,对角线不一定垂直.
2.已知EF过□ ABCD的对角线的交点O,交AD于点E,交BC于点F,已知AB=4,BC=5,OE=1.5,那么四边形EFCD的周长是( )
A.14 B.12 C.16 D.8
【解析】选B.由平行四边形的性质易证,AB=CD=4,BC=AD=5,
△AEO≌△CFO,所以OE=OF=1.5,AE=CF, 所以四边形EFCD的周长为:CD+DE+EF+FC=CD+BC+EF=4+5+3=12.
3.如图,□ ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )
A.3 B.6
C.12 D.24
【解析】选C.观察图形会发现,每一小块阴影三角形都
与它相对的三角形全等,则阴影部分的面积等于平行四
边形面积的一半.故S阴影= = ×6×4=12.
4.如图,□ ABCD中,AE⊥BD,∠EAD=60°,AE=2 cm,AC+BD=14 cm,则△OBC的周长是____cm.
【解析】在□ABCD中,BC=AD,OA=OC,OB=OD,
∵AE⊥BD,∠EAD=60°,AE=2 cm,∴AD=4 cm,BC=4cm,
∵AC+BD=14 cm,
∴OB+OC=7 cm,
∴△OBC的周长=OB+OC+BC=11 cm.
答案:11
通过本课时的学习,需要我们
1.知道平行四边形中心对称的特征.
2.掌握平行四边形对角线互相平分的性质并能利用这一性质进行计算或证明.
3.综合运用平行四边形的性质进行计算或证明.
