华东师大版八年级下册18.2平行四边形的判定(3) (共16张PPT)
文档属性
| 名称 | 华东师大版八年级下册18.2平行四边形的判定(3) (共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 13:26:50 | ||
图片预览





文档简介
华师大八年级下册
复习提问:
我们学习了哪些判定平行四边形的方法?
1、平行四边形的定义:
2、两组对边相等的四边形是平行四边形;
3、一组对边平行且相等的四边形是平行四边形 。
平行四边形的对角线具有什么性质?
平行四边形的对角线互相平分。
这个命题的逆命题是什么?
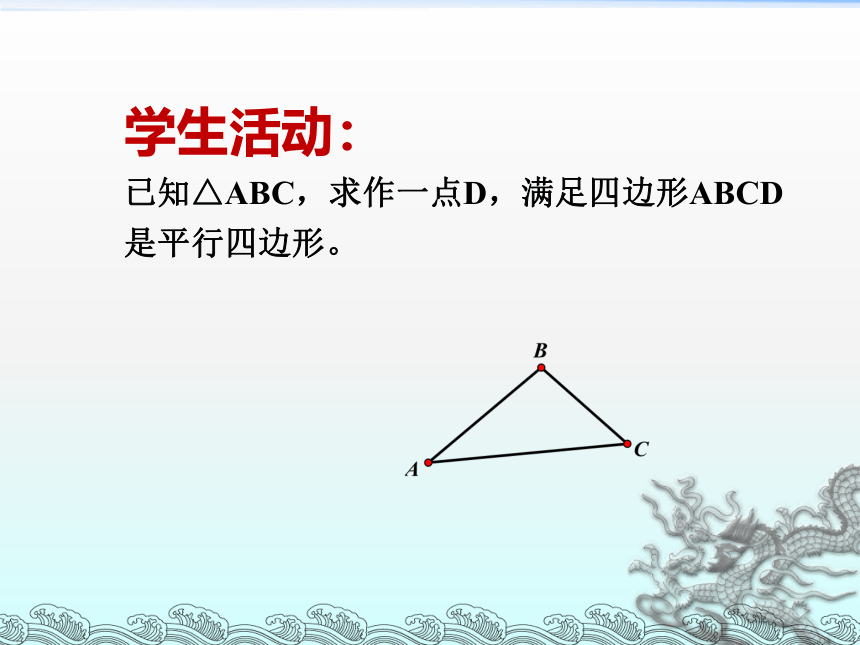
学生活动:
已知△ABC,求作一点D,满足四边形ABCD是平行四边形。
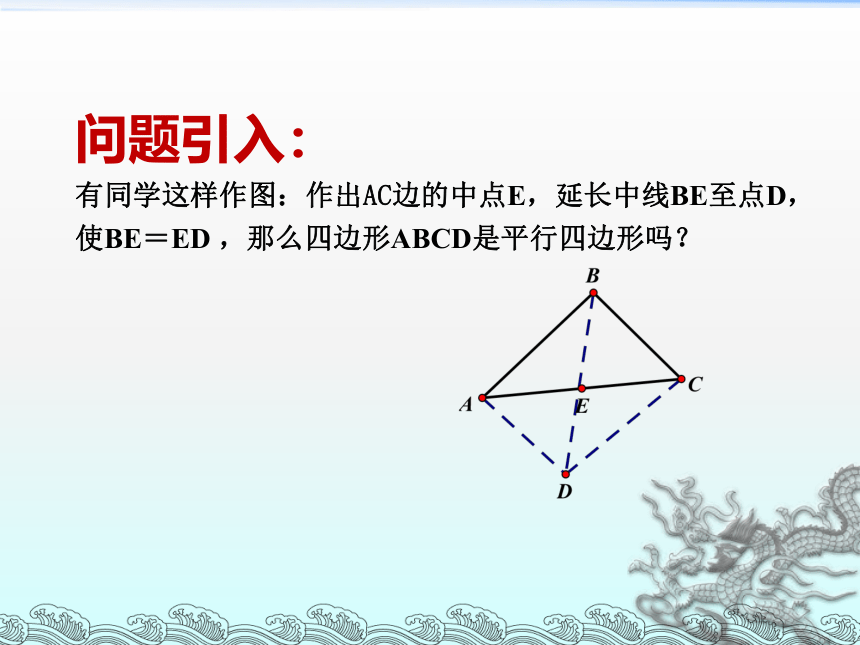
问题引入:
有同学这样作图:作出AC边的中点E,延长中线BE至点D,使BE=ED ,那么四边形ABCD是平行四边形吗?
动手操作,图形验证:
1、任意画两条相交直线m、n,记交点为O。
2、以O为圆心,分别在直线m、n上截取OB与OD,OA与OC,使OB=OD,OA=OC,顺次连结所得的四点,即得到一个两条对角线互相平分的四边形,它是平行四边形吗?
O
A
C
B
D
O
已知:如图,在四边形ABCD中,对角线AC和BD 相交于点O,AO=CO, BO=DO.
分析: 要证明四边形ABCD是平行四边形,可以用定义,也可以用平行四边形的两条判定方法,请你选择一种方法完成证明.
对角线互相平分的四边形是平行四边形.
证明:在△AOD和△COB中
∵AO=CO,BO=DO
∠AOD=∠COB
∴ △AOD≌△COB(SAS)
∴ AD=BC, ∠OAD=∠OCB
∴ AD∥BC
又∵AD=BC, AD∥BC
∴四边形ABCD是平行四边形
求证:四边形ABCD是平行四边形.
平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形.
例:如图,在 ABCD中,点E、F是对角线AC上的两点,且AE=CF,
求证:四边形BFDE是平行四边形.
例:如图,在 ABCD中,点E、F是对角线AC上的两点,且AE=CF,
求证:四边形BFDE是平行四边形.
分析 连结BD,交AC于点O,由于OB=OD
因此用“对角线互相平分的四边形是平行四边形”来证明四边形BFDE是平行四边形最为恰当,根据题意只需证明OE=OF.
证明:连结BD,交AC于点O
∵ 四边形ABCD是平行四边形
∴ OB=OD, OA=OC(平行四边形对角线互相平分)
∵ AE=FC,
∴ OA-AE=OC-CF
即 OE=OF,
∴ 四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形).
回答引入问题 :
有同学这样作图:作出AC边的中点E,延长中线BE至点D,使BE=ED ,那么四边形ABCD是平行四边形吗?
已知△ABC中,AB=5,BC=7,则AC边上的
中线BE的取值范围:_____
知识迁移:
归纳总结:
我们学会了多少种判定平行四边形的方法了?
1、平行四边形的定义:两组对边分别平行的 四边形是平行四边形。
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
4、对角线互相平分的四边形是平行四边形。
边
对角线
课堂检测:
1、补充一个合适的条件使⑴—⑶小题成立:
如图,四边形ABCD对角线AC、BD相交于点O
⑴若AB∥CD,______,则得 ABCD;
⑵若AB=CD,______,则得 ABCD;
⑶若AC=8,BD=10,AO=4,_______,则得 ABCD
2、 ABCD中,对角线AC、BD相交于点O,点E、F、G、H分别是OA、OC、OB、OD的中点,四边形EGFH___平行四边形。(填“是”或“不是”)
交流反思
本节课通过以上“猜想——作图验证——逻辑论证”,学生经历发现平行四边形判定定理的过程,能直接体验和掌握数学思维方法,获得数学学习的快乐.例题的讲解,学生可及时巩固新知识,同时培养了学生思维的灵活性,提高解决问题能力。对于练习中反馈的问题,教师及时改进教学,帮助学生澄清疑问,学通弄懂。
学生以小组为单位谈收获与疑惑。
归纳小结:
我们学会了多少种判定平行四边形的方法了?
1、平行四边形的定义:两组对边分别平行的
四边形是平行四边形。
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
4、对角线互相平分的四边形是平行四边形。
边
对角线
课后作业
今天作业!
1、熟记平行四边形的判定定理
2、(1) 教材习题18.2中第 3、4题.
(2)完成本课时对应练习.
复习提问:
我们学习了哪些判定平行四边形的方法?
1、平行四边形的定义:
2、两组对边相等的四边形是平行四边形;
3、一组对边平行且相等的四边形是平行四边形 。
平行四边形的对角线具有什么性质?
平行四边形的对角线互相平分。
这个命题的逆命题是什么?
学生活动:
已知△ABC,求作一点D,满足四边形ABCD是平行四边形。
问题引入:
有同学这样作图:作出AC边的中点E,延长中线BE至点D,使BE=ED ,那么四边形ABCD是平行四边形吗?
动手操作,图形验证:
1、任意画两条相交直线m、n,记交点为O。
2、以O为圆心,分别在直线m、n上截取OB与OD,OA与OC,使OB=OD,OA=OC,顺次连结所得的四点,即得到一个两条对角线互相平分的四边形,它是平行四边形吗?
O
A
C
B
D
O
已知:如图,在四边形ABCD中,对角线AC和BD 相交于点O,AO=CO, BO=DO.
分析: 要证明四边形ABCD是平行四边形,可以用定义,也可以用平行四边形的两条判定方法,请你选择一种方法完成证明.
对角线互相平分的四边形是平行四边形.
证明:在△AOD和△COB中
∵AO=CO,BO=DO
∠AOD=∠COB
∴ △AOD≌△COB(SAS)
∴ AD=BC, ∠OAD=∠OCB
∴ AD∥BC
又∵AD=BC, AD∥BC
∴四边形ABCD是平行四边形
求证:四边形ABCD是平行四边形.
平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形.
例:如图,在 ABCD中,点E、F是对角线AC上的两点,且AE=CF,
求证:四边形BFDE是平行四边形.
例:如图,在 ABCD中,点E、F是对角线AC上的两点,且AE=CF,
求证:四边形BFDE是平行四边形.
分析 连结BD,交AC于点O,由于OB=OD
因此用“对角线互相平分的四边形是平行四边形”来证明四边形BFDE是平行四边形最为恰当,根据题意只需证明OE=OF.
证明:连结BD,交AC于点O
∵ 四边形ABCD是平行四边形
∴ OB=OD, OA=OC(平行四边形对角线互相平分)
∵ AE=FC,
∴ OA-AE=OC-CF
即 OE=OF,
∴ 四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形).
回答引入问题 :
有同学这样作图:作出AC边的中点E,延长中线BE至点D,使BE=ED ,那么四边形ABCD是平行四边形吗?
已知△ABC中,AB=5,BC=7,则AC边上的
中线BE的取值范围:_____
知识迁移:
归纳总结:
我们学会了多少种判定平行四边形的方法了?
1、平行四边形的定义:两组对边分别平行的 四边形是平行四边形。
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
4、对角线互相平分的四边形是平行四边形。
边
对角线
课堂检测:
1、补充一个合适的条件使⑴—⑶小题成立:
如图,四边形ABCD对角线AC、BD相交于点O
⑴若AB∥CD,______,则得 ABCD;
⑵若AB=CD,______,则得 ABCD;
⑶若AC=8,BD=10,AO=4,_______,则得 ABCD
2、 ABCD中,对角线AC、BD相交于点O,点E、F、G、H分别是OA、OC、OB、OD的中点,四边形EGFH___平行四边形。(填“是”或“不是”)
交流反思
本节课通过以上“猜想——作图验证——逻辑论证”,学生经历发现平行四边形判定定理的过程,能直接体验和掌握数学思维方法,获得数学学习的快乐.例题的讲解,学生可及时巩固新知识,同时培养了学生思维的灵活性,提高解决问题能力。对于练习中反馈的问题,教师及时改进教学,帮助学生澄清疑问,学通弄懂。
学生以小组为单位谈收获与疑惑。
归纳小结:
我们学会了多少种判定平行四边形的方法了?
1、平行四边形的定义:两组对边分别平行的
四边形是平行四边形。
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
4、对角线互相平分的四边形是平行四边形。
边
对角线
课后作业
今天作业!
1、熟记平行四边形的判定定理
2、(1) 教材习题18.2中第 3、4题.
(2)完成本课时对应练习.
