华东师大版八年级下册数学:17.5函数及其图象 实践与探索课件 (共18张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学:17.5函数及其图象 实践与探索课件 (共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 607.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 13:26:09 | ||
图片预览






文档简介
华东师大版八年级(下册)
第17章 函数及其图象
实践与探索
一次函数的两种常见应用
课前复习: 旅客乘车按规定可随身携带一定重量的行李,如果超过规定,则需购行李票,该行李费y(元)是行李重量x(kg)的一次函数,如图所示。
求:(1)y与x之间的函数关系式;
(2)旅客最多可免费携带多少
行李的重量。
x(kg)
----------------
-------------
---------
-----
y(元)
90
60
10
5
O
1
6
1
6
解:(1)设一次函数关系式为y=kx+b(k≠0)
把x=60,y=5和x=90,y=10代入得
5=60k+b
10=90k+b
∴一次函数关系式为y=-x-5
(2)当y=0时,x=30
∴旅客最多可免费携带的行李重量是30kg 。
k=-
b=-5
(x≥30)
2
1
3
4
5
归纳:
由函数图象解答问题时,
首先、要明确横、纵轴表示的含义
其次、要读懂每一个折变线的交点的意义和自变量的取值范围
再次、函数图象的交点坐标表示两个图象上横、纵坐标都相同的点,同时一定要明确“点”的横、纵坐标所表示的内容。
一次函数的两种常见应用
名师点金:
一次函数的两种常见应用主要体现在解决实际问题和几何问题,能够从函数图象中得到需要的信息,并求出函数表达式从而解决实际问题和几何问题,是一次函数应用价值的体现,这种题型常与一些热点问题结合,考查学生综合分析问题、解决问题的能力.
1、黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象。(假设渔船与渔政船沿同一航线航行)
(1)直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.?
(2)求渔船和渔政船相遇时,两船与黄岩岛的距离.
利用函数图象解决实际问题
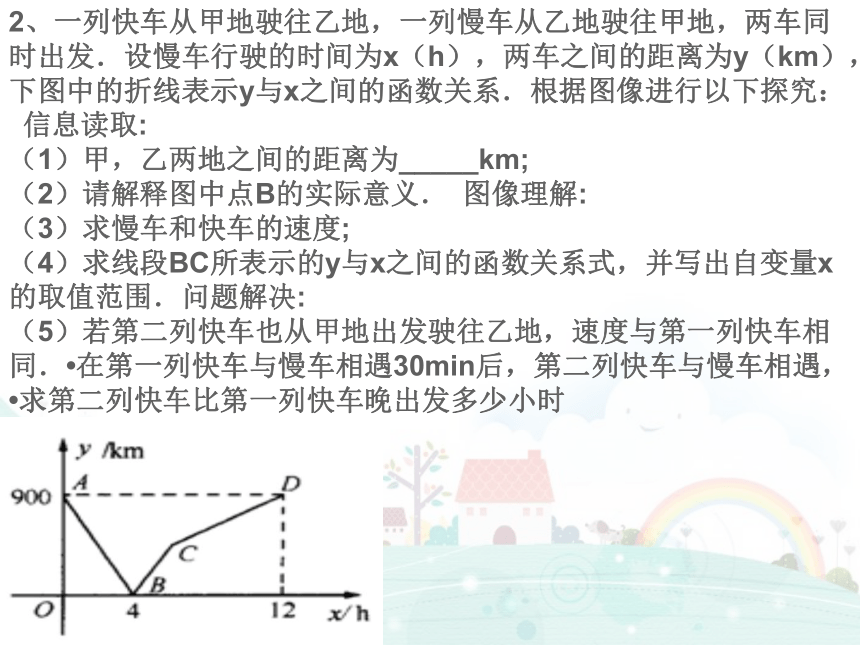
2、一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),下图中的折线表示y与x之间的函数关系.根据图像进行以下探究:?信息读取:
(1)甲,乙两地之间的距离为_____km;
(2)请解释图中点B的实际意义.?图像理解:
(3)求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围.问题解决:
(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.?在第一列快车与慢车相遇30min后,第二列快车与慢车相遇,?求第二列快车比第一列快车晚出发多少小时
3、 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:?
(1)写出A、B两地之间的距离;??
(2)求出点M的坐标,并解释该点坐标所表示的实际意义;??
(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.
实际问题中的分段函数
4.我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一个月用水10 t以内(包括10 t)的用户,每吨收水费a元;一个月用水超过10 t的用户,10 t水仍按每吨a元收费,超过10 t的部分,按每吨b(b>a)元收费.设一户居民月用水x t,应交水费y元,y与x之间的函数关系如图所示.
(1)求a的值;某户居民上月用水8 t,应交水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数表达式.
5.在长方形ABCD中,AB=3,BC=4,动点P从点A开始按A→B→C→D的方向运动到点D.如图,设动点P所经过的路程为x,△APD的面积为y.(当点P与点A或D重合时,y=0)
(1)写出y与x之间的函数表达式;
(2)画出此函数的图象.
利用分段函数解几何问题(分类讨论思想、数形结合思想)
利用图象解几何问题
6.如图①所示,正方形ABCD的边长为6 cm,动点P从点A出发,在正方形的边上沿A→B→C→D运动,设运动的时间为t(s),三角形APD的面积为S(cm2),S与t的函数图象如图②所示,请回答下列问题:
(1)点P在AB上运动的时间为________s,在CD上运动的速度为________cm/s,三角形APD的面积S的最大值为________cm2;
(2)求出点P在CD上运动时S与t之间的函数表达式;
(3)当t为何值时,三角形APD的面积为10 cm2?
利用一次函数解几何问题
练习:
小 结:
(1)看图应先看横轴和纵轴所表示的意义。
(2)“数”用“形”表示,由“形”想到数,数与 形结合,是我们数学学习中一种很重要的思想方法, 这就是数形结合法。
(3)函数图象不仅与函数解析式有关,
还直接与自变量的取值范围有关
板书:
第17章 函数及其图象
一次函数的两种常见应用
实践与探索
由函数图象解答问题时:
首先要明确横、纵轴表示的含义,
其次、要读懂每一个折变线的交点的意义和自变量的取值范围
再次、函数图象的交点坐标表示两个图象上横、纵坐标都相同的点,同时一定要明确“点”的横、纵坐标所表示的内容。
小 结:
(1)看图应先看横轴和纵轴所表示的意义。
(2)“数”用“形”表示,由“形”想到数,数与形结合,是我们数学学习中一种很 重要的思想方法,这就是数形结合法。
(3)函数图象不仅与函数解析式有关, 还直接与自变量的取值范围有关。
1、李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分种,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校。在课堂上,李老师请学生画出自行车行进路程S(千米)与行进时间t(小时)的函数图象的示意图,同学们画出的示意图如下,你认为正确的是( )
(A)
(B)
(C)
(D)
问:(1)如果李老师在修好车后减慢速度,但仍匀速行驶,
请问该选哪个答案。
(2)请修改题目,使其答案为A(或B)。
(3)如果S表示李老师离校的路程,请你画出它的函数示意图。
C
s s s s
t t t t
作业:
------
---------
----
-
●
●
●
O O O O
H x H x H x H x
3、某公司市场营销部的营销人员的个人收入与其每月的
销售量成一次函数关系,其图象如图所示,由图中给出
的信息可知,营销人员没有销售时
的收入是( )
(A)310 (B)300
(C)290 (D)280
B
2、如图所示,向高为H的圆柱形杯中注水,已知水杯底面半径为2,那么注水量y与水深x的函数关系的图象是( )
--------------------
---------------
--------
-------------
1300
800
O 1 2 销售量(单位:万件)
月收入(单位:元)
(A) (B) (C) (D)
--
A
4.甲、乙两地相距300 km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了________h;
(2)求线段DE对应的函数表达式;
(3)求轿车从甲地出发后经过多长时间追上货车.
工程问题
5.甲、乙两组工人同时加工某种零件,乙组在工作中有一段时间停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(h)之间的函数图象如图所示.
(1)求甲组加工零件的数量y与时间x之间的函数表达式.
(2)求乙组加工零件总量a的值.
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?
6.某种铂金饰品在甲、乙两个商店销售.甲店标价为477元/g,按标价出售,不优惠;乙店标价为530元/g,但若买的铂金饰品质量超过3 g,则超出部分可打八折.
(1)分别写出到甲、乙两个商店购买该种铂金饰品所需费用y(元)和质量x(g)之间的函数表达式;
(2)李阿姨要买一条质量不少于4 g且不超过10 g的此种铂金饰品,到哪个商店购买合算?
7.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示,则下列结论:
①A,B两城相距300 km;
②乙车比甲车晚出发1 h,却早到1 h;
③乙车出发后2.5 h追上甲车;
④当甲、乙两车相距50 km时,t=或.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
第17章 函数及其图象
实践与探索
一次函数的两种常见应用
课前复习: 旅客乘车按规定可随身携带一定重量的行李,如果超过规定,则需购行李票,该行李费y(元)是行李重量x(kg)的一次函数,如图所示。
求:(1)y与x之间的函数关系式;
(2)旅客最多可免费携带多少
行李的重量。
x(kg)
----------------
-------------
---------
-----
y(元)
90
60
10
5
O
1
6
1
6
解:(1)设一次函数关系式为y=kx+b(k≠0)
把x=60,y=5和x=90,y=10代入得
5=60k+b
10=90k+b
∴一次函数关系式为y=-x-5
(2)当y=0时,x=30
∴旅客最多可免费携带的行李重量是30kg 。
k=-
b=-5
(x≥30)
2
1
3
4
5
归纳:
由函数图象解答问题时,
首先、要明确横、纵轴表示的含义
其次、要读懂每一个折变线的交点的意义和自变量的取值范围
再次、函数图象的交点坐标表示两个图象上横、纵坐标都相同的点,同时一定要明确“点”的横、纵坐标所表示的内容。
一次函数的两种常见应用
名师点金:
一次函数的两种常见应用主要体现在解决实际问题和几何问题,能够从函数图象中得到需要的信息,并求出函数表达式从而解决实际问题和几何问题,是一次函数应用价值的体现,这种题型常与一些热点问题结合,考查学生综合分析问题、解决问题的能力.
1、黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象。(假设渔船与渔政船沿同一航线航行)
(1)直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.?
(2)求渔船和渔政船相遇时,两船与黄岩岛的距离.
利用函数图象解决实际问题
2、一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),下图中的折线表示y与x之间的函数关系.根据图像进行以下探究:?信息读取:
(1)甲,乙两地之间的距离为_____km;
(2)请解释图中点B的实际意义.?图像理解:
(3)求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围.问题解决:
(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.?在第一列快车与慢车相遇30min后,第二列快车与慢车相遇,?求第二列快车比第一列快车晚出发多少小时
3、 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:?
(1)写出A、B两地之间的距离;??
(2)求出点M的坐标,并解释该点坐标所表示的实际意义;??
(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.
实际问题中的分段函数
4.我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一个月用水10 t以内(包括10 t)的用户,每吨收水费a元;一个月用水超过10 t的用户,10 t水仍按每吨a元收费,超过10 t的部分,按每吨b(b>a)元收费.设一户居民月用水x t,应交水费y元,y与x之间的函数关系如图所示.
(1)求a的值;某户居民上月用水8 t,应交水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数表达式.
5.在长方形ABCD中,AB=3,BC=4,动点P从点A开始按A→B→C→D的方向运动到点D.如图,设动点P所经过的路程为x,△APD的面积为y.(当点P与点A或D重合时,y=0)
(1)写出y与x之间的函数表达式;
(2)画出此函数的图象.
利用分段函数解几何问题(分类讨论思想、数形结合思想)
利用图象解几何问题
6.如图①所示,正方形ABCD的边长为6 cm,动点P从点A出发,在正方形的边上沿A→B→C→D运动,设运动的时间为t(s),三角形APD的面积为S(cm2),S与t的函数图象如图②所示,请回答下列问题:
(1)点P在AB上运动的时间为________s,在CD上运动的速度为________cm/s,三角形APD的面积S的最大值为________cm2;
(2)求出点P在CD上运动时S与t之间的函数表达式;
(3)当t为何值时,三角形APD的面积为10 cm2?
利用一次函数解几何问题
练习:
小 结:
(1)看图应先看横轴和纵轴所表示的意义。
(2)“数”用“形”表示,由“形”想到数,数与 形结合,是我们数学学习中一种很重要的思想方法, 这就是数形结合法。
(3)函数图象不仅与函数解析式有关,
还直接与自变量的取值范围有关
板书:
第17章 函数及其图象
一次函数的两种常见应用
实践与探索
由函数图象解答问题时:
首先要明确横、纵轴表示的含义,
其次、要读懂每一个折变线的交点的意义和自变量的取值范围
再次、函数图象的交点坐标表示两个图象上横、纵坐标都相同的点,同时一定要明确“点”的横、纵坐标所表示的内容。
小 结:
(1)看图应先看横轴和纵轴所表示的意义。
(2)“数”用“形”表示,由“形”想到数,数与形结合,是我们数学学习中一种很 重要的思想方法,这就是数形结合法。
(3)函数图象不仅与函数解析式有关, 还直接与自变量的取值范围有关。
1、李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分种,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校。在课堂上,李老师请学生画出自行车行进路程S(千米)与行进时间t(小时)的函数图象的示意图,同学们画出的示意图如下,你认为正确的是( )
(A)
(B)
(C)
(D)
问:(1)如果李老师在修好车后减慢速度,但仍匀速行驶,
请问该选哪个答案。
(2)请修改题目,使其答案为A(或B)。
(3)如果S表示李老师离校的路程,请你画出它的函数示意图。
C
s s s s
t t t t
作业:
------
---------
----
-
●
●
●
O O O O
H x H x H x H x
3、某公司市场营销部的营销人员的个人收入与其每月的
销售量成一次函数关系,其图象如图所示,由图中给出
的信息可知,营销人员没有销售时
的收入是( )
(A)310 (B)300
(C)290 (D)280
B
2、如图所示,向高为H的圆柱形杯中注水,已知水杯底面半径为2,那么注水量y与水深x的函数关系的图象是( )
--------------------
---------------
--------
-------------
1300
800
O 1 2 销售量(单位:万件)
月收入(单位:元)
(A) (B) (C) (D)
--
A
4.甲、乙两地相距300 km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了________h;
(2)求线段DE对应的函数表达式;
(3)求轿车从甲地出发后经过多长时间追上货车.
工程问题
5.甲、乙两组工人同时加工某种零件,乙组在工作中有一段时间停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(h)之间的函数图象如图所示.
(1)求甲组加工零件的数量y与时间x之间的函数表达式.
(2)求乙组加工零件总量a的值.
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?
6.某种铂金饰品在甲、乙两个商店销售.甲店标价为477元/g,按标价出售,不优惠;乙店标价为530元/g,但若买的铂金饰品质量超过3 g,则超出部分可打八折.
(1)分别写出到甲、乙两个商店购买该种铂金饰品所需费用y(元)和质量x(g)之间的函数表达式;
(2)李阿姨要买一条质量不少于4 g且不超过10 g的此种铂金饰品,到哪个商店购买合算?
7.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示,则下列结论:
①A,B两城相距300 km;
②乙车比甲车晚出发1 h,却早到1 h;
③乙车出发后2.5 h追上甲车;
④当甲、乙两车相距50 km时,t=或.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
