华东师大版八年级下册数学课件:18.2从边的角度判定平行四边形 (共18张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学课件:18.2从边的角度判定平行四边形 (共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 691.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 21:16:25 | ||
图片预览





文档简介
1、探索并掌握平行四边形的判定定理。
2、运用判定定理解决问题。
3、在观察、探究中,进一步培养自己的 数学推理能力。
我们已学过哪些方法可以来判定一个四边形是平行四边形?
定义法:两组对边分别平行的四边形叫平行四边形.
判定定理1:两组对边分别相等的四边形是平行四边形.
知识回顾
还有没有其他的方法?
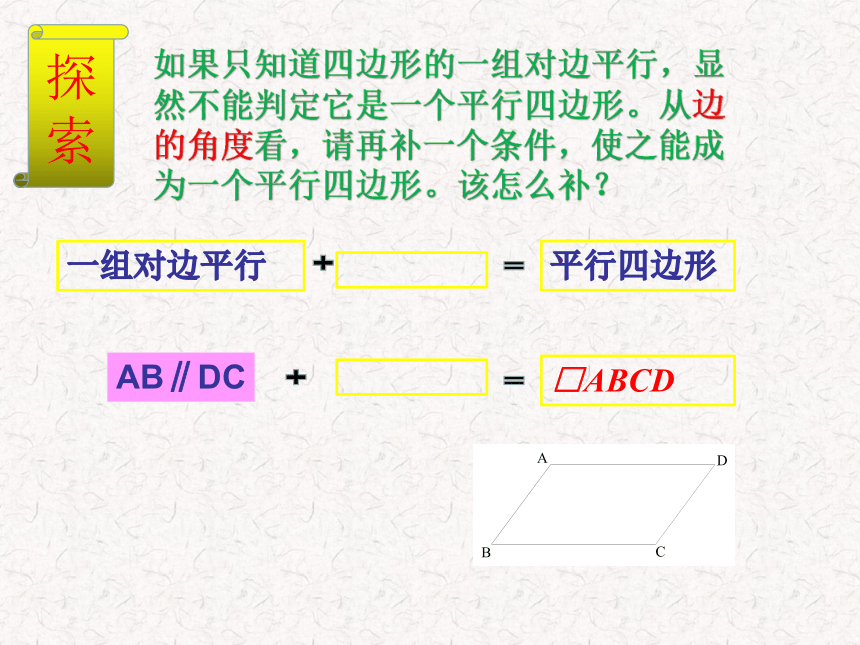
AB∥DC
如果只知道四边形的一组对边平行,显然不能判定它是一个平行四边形。从边的角度看,请再补一个条件,使之能成为一个平行四边形。该怎么补?
探索
平行四边形
AB∥DC
AD=BC
猜想
一组对边平行,另一组对边相等的四边形是平行四边形。(真/假?)
?
假命题
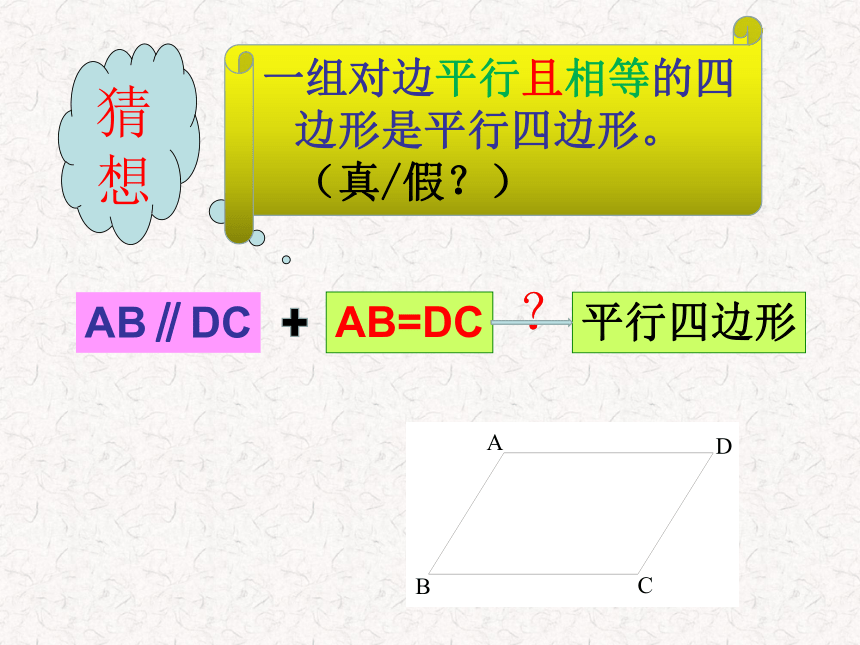
猜想
一组对边平行且相等的四边形是平行四边形。(真/假?)
AB∥DC
平行四边形
AB=DC
?
1.画一画:
作一个一组对边平行且相等的四边形.
2.观察比较,你作出的四边形是什么样的四边形,并与同学交流.
动手试一试
已知:在四边形ABCD中, AB=CD,AB∥CD
求证:四边形ABCD是平行四边形
A
B
C
D
分
析
AB=CD,AB∥CD
AB=CD,AD=BC
?
全等三角形
推理验证
还能用其他方法证明吗?
证明:连结AC,
∵ AB∥CD,
∴ ∠1=∠2(两直线平行,内错角相等),
又∵ AB=CD ,AC=AC,
∴ △ABC≌ △CDA(S.A.S.),
∴ AD=BC (全等三角形的性质),
∴ 四边形ABCD是平行四边形
(两组对边分别 相等 的四边形是平行四边形).
∴ ∠3=∠4(全等三角形的性质),
∴ AD∥BC(内错角相等,两直线平行)
∴ 四边形ABCD是平行四边形
(两组对边分别 平行 的四边形是平行四边形).
已知:在四边形ABCD中, AB=CD,AB∥CD
求证:四边形ABCD是平行四边形.
A
B
C
D
2
1
3
4
小结
转化
四边形 问题
三角形 问题
:
这正是我们解决数学问题的基本步骤。
小结
观察猜想
操作感知
推理验证
A
B
C
D
符号语言:
平行四边形判定定理2 : 一组对边平行且相等的四边形是平行四边形。
∵ AB=CD,AB∥CD,
∴ 四边形ABCD是平行四边形.
在四边形ABCD,
用3分钟时间记忆判定定理2及其符号语言;并复述给你的同伴。
如图,在平行四边形ABCD中,E、F分别是边BC和AD上的两点,且AF=CE。
求证:四边形AECF为平行四边形.
B
A
C
D
F
E
例题分析
根据条件选择简捷的方法
B
随堂演练
5
(1)若AB∥CD,补充条件_____, 使四边形ABCD为平行四边形。
3,如图,四边形ABCD中
(2)若AD=CB,补充条件_____,使四边形ABCD为平行四边形。
AD∥CB
或者AB=CD
AD∥CB
或者AB=CD
C
B
D
A
4、在平面直角坐标系上,若以A(-1,0)
B(2,0)C(0,1)三点为顶点画平行
四边形,则第四个点 不可能在( )
A.第一象限 B. 第二象限
C. 第三象限 D. 第四象限
C
文字语言
图形语言
符号语言
定义法
两组对边分别平行的四边形是平行四边形
∵ AD∥CB,
AB∥DC
∴ 四边形ABCD 是平行四边形
平行四边形判定定理1
两组对边分别相等的四边形是平行四边形
∵ AD=CB,
AB=DC
∴ 四边形ABCD是平行四边形
平行四边形判定定理2
一组对边平行且相等的四边形是平行四边形
∵AB//CD,
AB =CD
∴四边形ABCD是平行四边形
A
D
B
C
知识梳理
---平行四边形的判定方法
作业
1,课本P85-2,3(交)
2,课课练P55
2、运用判定定理解决问题。
3、在观察、探究中,进一步培养自己的 数学推理能力。
我们已学过哪些方法可以来判定一个四边形是平行四边形?
定义法:两组对边分别平行的四边形叫平行四边形.
判定定理1:两组对边分别相等的四边形是平行四边形.
知识回顾
还有没有其他的方法?
AB∥DC
如果只知道四边形的一组对边平行,显然不能判定它是一个平行四边形。从边的角度看,请再补一个条件,使之能成为一个平行四边形。该怎么补?
探索
平行四边形
AB∥DC
AD=BC
猜想
一组对边平行,另一组对边相等的四边形是平行四边形。(真/假?)
?
假命题
猜想
一组对边平行且相等的四边形是平行四边形。(真/假?)
AB∥DC
平行四边形
AB=DC
?
1.画一画:
作一个一组对边平行且相等的四边形.
2.观察比较,你作出的四边形是什么样的四边形,并与同学交流.
动手试一试
已知:在四边形ABCD中, AB=CD,AB∥CD
求证:四边形ABCD是平行四边形
A
B
C
D
分
析
AB=CD,AB∥CD
AB=CD,AD=BC
?
全等三角形
推理验证
还能用其他方法证明吗?
证明:连结AC,
∵ AB∥CD,
∴ ∠1=∠2(两直线平行,内错角相等),
又∵ AB=CD ,AC=AC,
∴ △ABC≌ △CDA(S.A.S.),
∴ AD=BC (全等三角形的性质),
∴ 四边形ABCD是平行四边形
(两组对边分别 相等 的四边形是平行四边形).
∴ ∠3=∠4(全等三角形的性质),
∴ AD∥BC(内错角相等,两直线平行)
∴ 四边形ABCD是平行四边形
(两组对边分别 平行 的四边形是平行四边形).
已知:在四边形ABCD中, AB=CD,AB∥CD
求证:四边形ABCD是平行四边形.
A
B
C
D
2
1
3
4
小结
转化
四边形 问题
三角形 问题
:
这正是我们解决数学问题的基本步骤。
小结
观察猜想
操作感知
推理验证
A
B
C
D
符号语言:
平行四边形判定定理2 : 一组对边平行且相等的四边形是平行四边形。
∵ AB=CD,AB∥CD,
∴ 四边形ABCD是平行四边形.
在四边形ABCD,
用3分钟时间记忆判定定理2及其符号语言;并复述给你的同伴。
如图,在平行四边形ABCD中,E、F分别是边BC和AD上的两点,且AF=CE。
求证:四边形AECF为平行四边形.
B
A
C
D
F
E
例题分析
根据条件选择简捷的方法
B
随堂演练
5
(1)若AB∥CD,补充条件_____, 使四边形ABCD为平行四边形。
3,如图,四边形ABCD中
(2)若AD=CB,补充条件_____,使四边形ABCD为平行四边形。
AD∥CB
或者AB=CD
AD∥CB
或者AB=CD
C
B
D
A
4、在平面直角坐标系上,若以A(-1,0)
B(2,0)C(0,1)三点为顶点画平行
四边形,则第四个点 不可能在( )
A.第一象限 B. 第二象限
C. 第三象限 D. 第四象限
C
文字语言
图形语言
符号语言
定义法
两组对边分别平行的四边形是平行四边形
∵ AD∥CB,
AB∥DC
∴ 四边形ABCD 是平行四边形
平行四边形判定定理1
两组对边分别相等的四边形是平行四边形
∵ AD=CB,
AB=DC
∴ 四边形ABCD是平行四边形
平行四边形判定定理2
一组对边平行且相等的四边形是平行四边形
∵AB//CD,
AB =CD
∴四边形ABCD是平行四边形
A
D
B
C
知识梳理
---平行四边形的判定方法
作业
1,课本P85-2,3(交)
2,课课练P55
