华东师大版九年级数学下册27.2.1:点和圆的位置关系 课件(共20张PPT)
文档属性
| 名称 | 华东师大版九年级数学下册27.2.1:点和圆的位置关系 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 973.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 12:54:33 | ||
图片预览






文档简介
生活中的数学
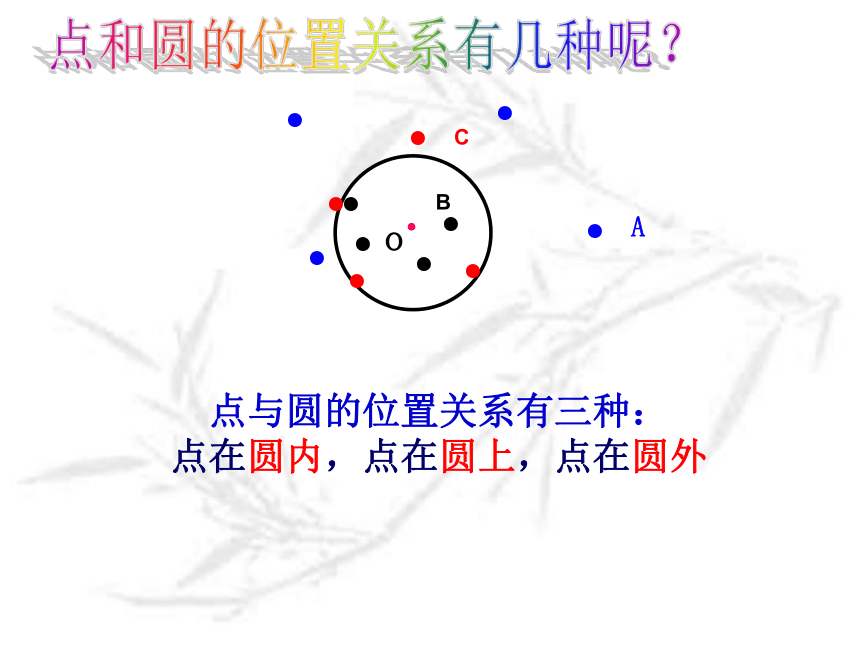
如果箭看成点,箭靶看成圆,那么上面情境反映了点与圆的位置关系。
.
o
.
.
.C
.
.
.
. B
.
.A
.
.
.
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外
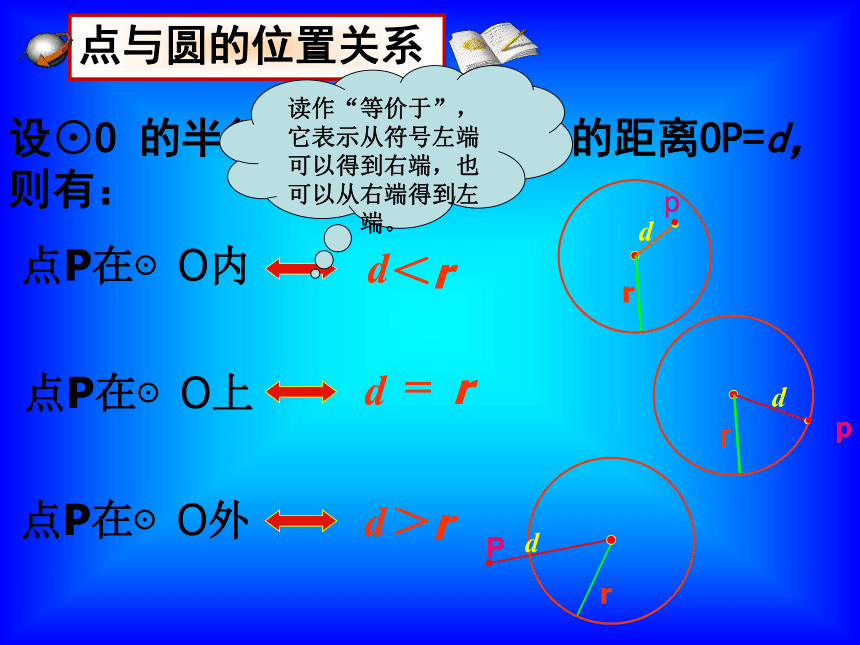
设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
点P在⊙O上
点P在⊙O外
点与圆的位置关系
d
d
d
r
p
d
p
r
d
P
r
d
读作“等价于”,它表示从符号左端可以得到右端,也可以从右端得到左端。
<
r
r
=
>
r
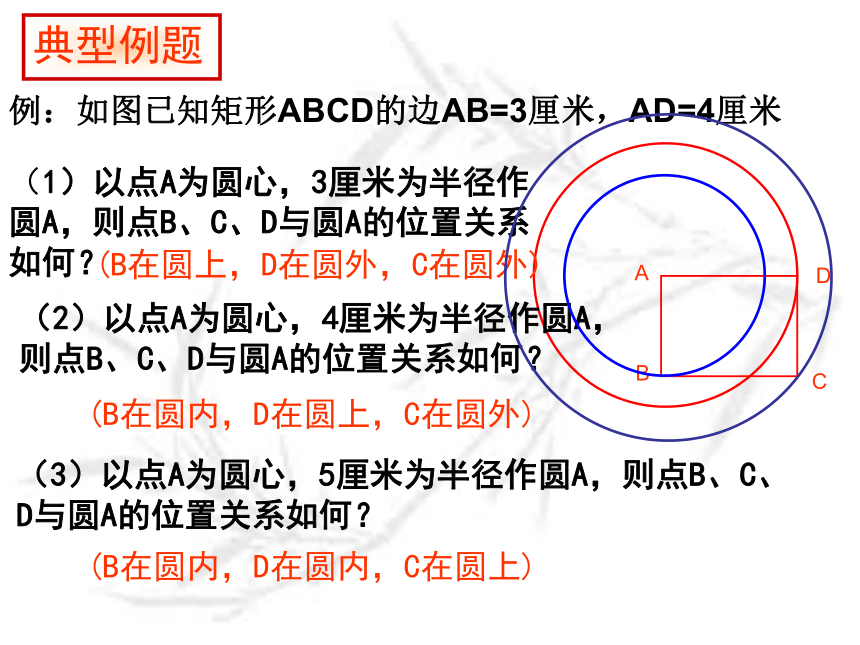
例:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
典型例题
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
练一练
1、⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 。
2、⊙O的半径6cm,当OP=6时,点P在 ;
当OP 时点P在圆内;当OP 时,点P不在圆外。
3、正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A ;点C在⊙A ;点D在⊙A 。
圆内
圆上
圆外
圆上
<6
≤6
上
外
上
4、已知AB为⊙O的直径P为⊙O 上任意一点,则点P关于AB的对称点P′与⊙O的位置为( )
(A)在⊙O内 (B)在⊙O 外 (C)在⊙O 上 (D)不能确定
c
5.已知⊙O的面积为25π:
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上;
(4)若点P不在圆外,则PO__________。
圆外
圆内
5
≤5
·
2cm
3cm
画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
O
1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
探究与实践
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离
2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点?
探究与实践
●O
● O
●O
●O
A
B
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
无数个。它们的圆心都在线段AB的垂直平分线上。
3、平面上有三点A、B、C,经过A、B、C三点的圆有几个?圆心在哪里?
归纳结论:
不在同一条直线上的三个点确定一个圆。
探究与实践
┓
●B
●C
(2)经过B,C两点的圆的圆心在线段AB的垂直平分线上.
┏
●A
(3)经过A,B,C三点的圆的圆心应该这两条垂直平分线的交点O的位置.
所以圆O就是所求作
●O
(1)经过A,B两点的圆的圆心在线段AB的垂直平分线上.
作法:
经过同一条直线三个点能作出一个圆吗?
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A、B、C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
经过三角形三个顶点可以画一个圆,并且只能画一个.
一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
经过三角形三个顶点的圆叫做三角形的外接圆。
三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。
这个三角形叫做这个圆的内接三角形。
三角形外接圆的圆心叫做这个三角形的外心。
●O
A
B
C
有关概念
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
做一做
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
思考: 如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心.
D
A
B
C
O
∵A、B两点在圆上,所以圆心必与A、B两点的距离相等,
又∵和一条线段的两个端点距离相等的点在这条线段的垂直平分线上,
∴圆心在CD所在的直线上,因此可以做任意两条直径,它们的交点为圆心.
练一练
1、判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( ).
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( )
2、若一个三角形的外心在一边上,则此三角形的 形状为( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形
√
×
×
√
B
1、如图,已知 Rt⊿ABC 中 ,
若 AC=12cm,BC=5cm,
求的外接圆半径。
C
B
A
如图,等腰⊿ABC中, ,
,求外接圆的半径。
O
A
D
C
B
如何解决“破镜重圆”的问题:
A
B
C
O
圆心一定在弦的垂直平分线上
1、点和圆的位置关系有几种?
dd=r
d>r
⑴点在圆内
·
P
⑵点在圆上
·
P
⑶点在圆外
·
P
(令OP=d )
2、定理:不在同一直线上的三点确定一个圆.
如果箭看成点,箭靶看成圆,那么上面情境反映了点与圆的位置关系。
.
o
.
.
.C
.
.
.
. B
.
.A
.
.
.
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外
设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
点P在⊙O上
点P在⊙O外
点与圆的位置关系
d
d
d
r
p
d
p
r
d
P
r
d
读作“等价于”,它表示从符号左端可以得到右端,也可以从右端得到左端。
<
r
r
=
>
r
例:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
典型例题
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
练一练
1、⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 。
2、⊙O的半径6cm,当OP=6时,点P在 ;
当OP 时点P在圆内;当OP 时,点P不在圆外。
3、正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A ;点C在⊙A ;点D在⊙A 。
圆内
圆上
圆外
圆上
<6
≤6
上
外
上
4、已知AB为⊙O的直径P为⊙O 上任意一点,则点P关于AB的对称点P′与⊙O的位置为( )
(A)在⊙O内 (B)在⊙O 外 (C)在⊙O 上 (D)不能确定
c
5.已知⊙O的面积为25π:
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上;
(4)若点P不在圆外,则PO__________。
圆外
圆内
5
≤5
·
2cm
3cm
画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
O
1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
探究与实践
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离
2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点?
探究与实践
●O
● O
●O
●O
A
B
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
无数个。它们的圆心都在线段AB的垂直平分线上。
3、平面上有三点A、B、C,经过A、B、C三点的圆有几个?圆心在哪里?
归纳结论:
不在同一条直线上的三个点确定一个圆。
探究与实践
┓
●B
●C
(2)经过B,C两点的圆的圆心在线段AB的垂直平分线上.
┏
●A
(3)经过A,B,C三点的圆的圆心应该这两条垂直平分线的交点O的位置.
所以圆O就是所求作
●O
(1)经过A,B两点的圆的圆心在线段AB的垂直平分线上.
作法:
经过同一条直线三个点能作出一个圆吗?
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A、B、C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
经过三角形三个顶点可以画一个圆,并且只能画一个.
一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
经过三角形三个顶点的圆叫做三角形的外接圆。
三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。
这个三角形叫做这个圆的内接三角形。
三角形外接圆的圆心叫做这个三角形的外心。
●O
A
B
C
有关概念
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
做一做
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
思考: 如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心.
D
A
B
C
O
∵A、B两点在圆上,所以圆心必与A、B两点的距离相等,
又∵和一条线段的两个端点距离相等的点在这条线段的垂直平分线上,
∴圆心在CD所在的直线上,因此可以做任意两条直径,它们的交点为圆心.
练一练
1、判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( ).
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( )
2、若一个三角形的外心在一边上,则此三角形的 形状为( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形
√
×
×
√
B
1、如图,已知 Rt⊿ABC 中 ,
若 AC=12cm,BC=5cm,
求的外接圆半径。
C
B
A
如图,等腰⊿ABC中, ,
,求外接圆的半径。
O
A
D
C
B
如何解决“破镜重圆”的问题:
A
B
C
O
圆心一定在弦的垂直平分线上
1、点和圆的位置关系有几种?
d
d>r
⑴点在圆内
·
P
⑵点在圆上
·
P
⑶点在圆外
·
P
(令OP=d )
2、定理:不在同一直线上的三点确定一个圆.
