华东师大版七年级下册数学 7.2 代入法解二元一次方程组(2) 课件(共18张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 7.2 代入法解二元一次方程组(2) 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 672.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 13:29:25 | ||
图片预览






文档简介
华东师大版七年级下册
第7章 二元一次方程组
7.2 二元一次方程组的解法(第1课时)
7.2二元一次方程组的解法
代入法(1)
1.什么叫做二元一次方程?
2.什么叫做二元一次方程组?
3.什么叫做二元一次方程组的解?
每个方程都有两个未知数,并且未知数的次数都是1,这样的方程叫做二元一次方程。
x+y=7 ①
3x+y=17 ②
y=4x ①
y-x=20000×30% ②
把两个二元一次方程合在一起,就组成了一个二元一次方程组。
把能使方程组中每一个方程的左右两边的值都相等,像这样的两个未知数的值叫做二元一次方程组的解。
如
x=2000
y=8000
x=5
y=2
根据方程的变形规则同学们能否把3x+y=7改写成用x的代数式表示y的形式?
Y=7-3x
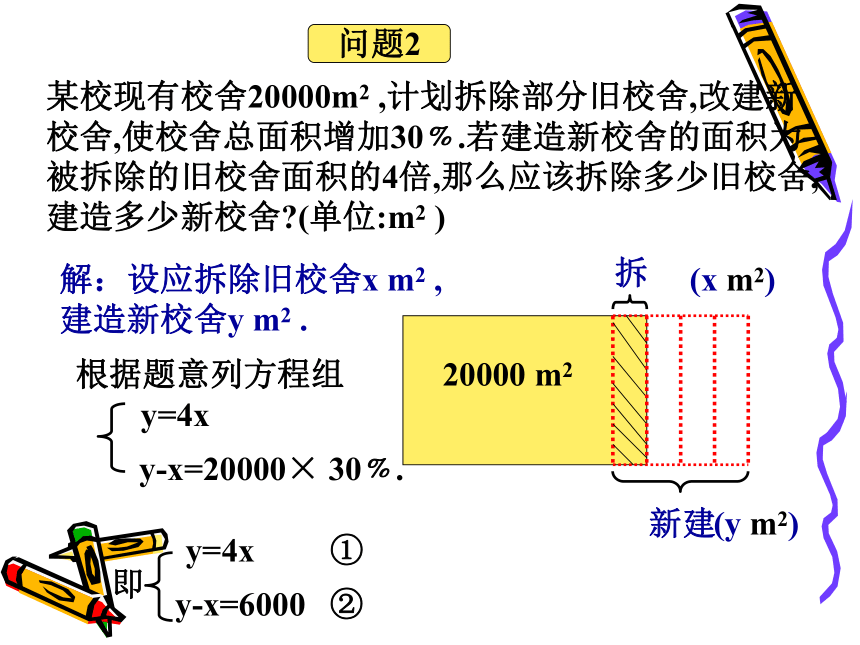
问题2
某校现有校舍20000m2 ,计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30﹪.若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位:m2 )
拆
新建
解:设应拆除旧校舍x m2 ,建造新校舍y m2 .
根据题意列方程组
(x m2)
(y m2)
20000 m2
y=4x
y-x=20000× 30﹪.
即
y-x=6000
y=4x
①
②
y= 4x
y -x=6000
解方程组
①
②
解:把① 代入②,得
4x -x=6000,
3x =6000,
x =2000.
把x =2000代入①,得
y= 4×2000,
y=8000.
所以
x =2000,
y=8000.
例1
x+y=5 ①
y=4x ②
解:把②代入① ,得
x+4x=5
5x=5
x=1
把x=1代入②得
y=4
x=1
所以
y=4
思路与方法:
二元一次方程组
代入消去一个未知数
一元一次方程
(其中含有用一个未知数表示另一个未知数的方程)
请同学们用上面学到的方法解这个方程组
“消元”
x=3y+2,
x=3×1+2
解方程组:
①
②
解:把① 代入②,得
把y=1代入①,得
y= 1.
所以
x =5,
y=1.
(1)
( )+3y=8,
3y+2
6y+2=8,
6y=8-2,
6y=6,
x=5.
x+3y=8.
练一练
y=7-5x.
解方程组:
①
②
解:把 代入 ,得
把x=2代入 ,得
所以
x =2,
y=-3.
(2)
4x-3y=17,
①
②
4x-3( )=17,
7-5x
4x
4x+15x=17+21,
19x =38,
x=2
②
y=7 - 5×2,
y=-3.
练一练
-21+15x
=17,
例1 解方程组
①
②
解 由①得 ③
将 ③代入 ②,得
即
将 代入③ ,得
1、通过适当变形,把其中一个未知数用另一个未知数的形式表示;
选择适当途径
2、直接代入消元,化二元一次方程组为一元一次方程,进而求解;
3、新问题、新知识 旧问题、旧知识。
思考:2、解方程组
①
②
(检验)
1、解二元一次方程组的思想方法:通过代入的方法,达到消元的目的,化二元一次方程组为一元一次方程求解;
2、用代入消元法解二元一次方程组的一般步骤。
P36页 习题7.2 第1题 (1),(2)
课后练习
若(x-2y+1)2+(x+2y-3)2=0, 则x、y的值是x=___,y=___。
谢谢大家
生命里最重要的事情是要有个远大的目标,并借助才能与坚毅来达成它.
第7章 二元一次方程组
7.2 二元一次方程组的解法(第1课时)
7.2二元一次方程组的解法
代入法(1)
1.什么叫做二元一次方程?
2.什么叫做二元一次方程组?
3.什么叫做二元一次方程组的解?
每个方程都有两个未知数,并且未知数的次数都是1,这样的方程叫做二元一次方程。
x+y=7 ①
3x+y=17 ②
y=4x ①
y-x=20000×30% ②
把两个二元一次方程合在一起,就组成了一个二元一次方程组。
把能使方程组中每一个方程的左右两边的值都相等,像这样的两个未知数的值叫做二元一次方程组的解。
如
x=2000
y=8000
x=5
y=2
根据方程的变形规则同学们能否把3x+y=7改写成用x的代数式表示y的形式?
Y=7-3x
问题2
某校现有校舍20000m2 ,计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30﹪.若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位:m2 )
拆
新建
解:设应拆除旧校舍x m2 ,建造新校舍y m2 .
根据题意列方程组
(x m2)
(y m2)
20000 m2
y=4x
y-x=20000× 30﹪.
即
y-x=6000
y=4x
①
②
y= 4x
y -x=6000
解方程组
①
②
解:把① 代入②,得
4x -x=6000,
3x =6000,
x =2000.
把x =2000代入①,得
y= 4×2000,
y=8000.
所以
x =2000,
y=8000.
例1
x+y=5 ①
y=4x ②
解:把②代入① ,得
x+4x=5
5x=5
x=1
把x=1代入②得
y=4
x=1
所以
y=4
思路与方法:
二元一次方程组
代入消去一个未知数
一元一次方程
(其中含有用一个未知数表示另一个未知数的方程)
请同学们用上面学到的方法解这个方程组
“消元”
x=3y+2,
x=3×1+2
解方程组:
①
②
解:把① 代入②,得
把y=1代入①,得
y= 1.
所以
x =5,
y=1.
(1)
( )+3y=8,
3y+2
6y+2=8,
6y=8-2,
6y=6,
x=5.
x+3y=8.
练一练
y=7-5x.
解方程组:
①
②
解:把 代入 ,得
把x=2代入 ,得
所以
x =2,
y=-3.
(2)
4x-3y=17,
①
②
4x-3( )=17,
7-5x
4x
4x+15x=17+21,
19x =38,
x=2
②
y=7 - 5×2,
y=-3.
练一练
-21+15x
=17,
例1 解方程组
①
②
解 由①得 ③
将 ③代入 ②,得
即
将 代入③ ,得
1、通过适当变形,把其中一个未知数用另一个未知数的形式表示;
选择适当途径
2、直接代入消元,化二元一次方程组为一元一次方程,进而求解;
3、新问题、新知识 旧问题、旧知识。
思考:2、解方程组
①
②
(检验)
1、解二元一次方程组的思想方法:通过代入的方法,达到消元的目的,化二元一次方程组为一元一次方程求解;
2、用代入消元法解二元一次方程组的一般步骤。
P36页 习题7.2 第1题 (1),(2)
课后练习
若(x-2y+1)2+(x+2y-3)2=0, 则x、y的值是x=___,y=___。
谢谢大家
生命里最重要的事情是要有个远大的目标,并借助才能与坚毅来达成它.
