华东师大版七年级下册数学:9.2 多边形的外角和 (共18张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学:9.2 多边形的外角和 (共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 00:00:00 | ||
图片预览




文档简介
9.2多边形的内角和与外角
第二课时
华东师大版七年级(下册)
多边形的外角和
9.2多边形的内角和与外角
第二课时
华东师大版七年级(下册)
多边形的外角和
温故知新
一、n 边形的内角和为__________
二、求七边形的内角和的度数.
(n-2) 180 °
解:(n-2)×180°
=(7-2)×180°
=900°
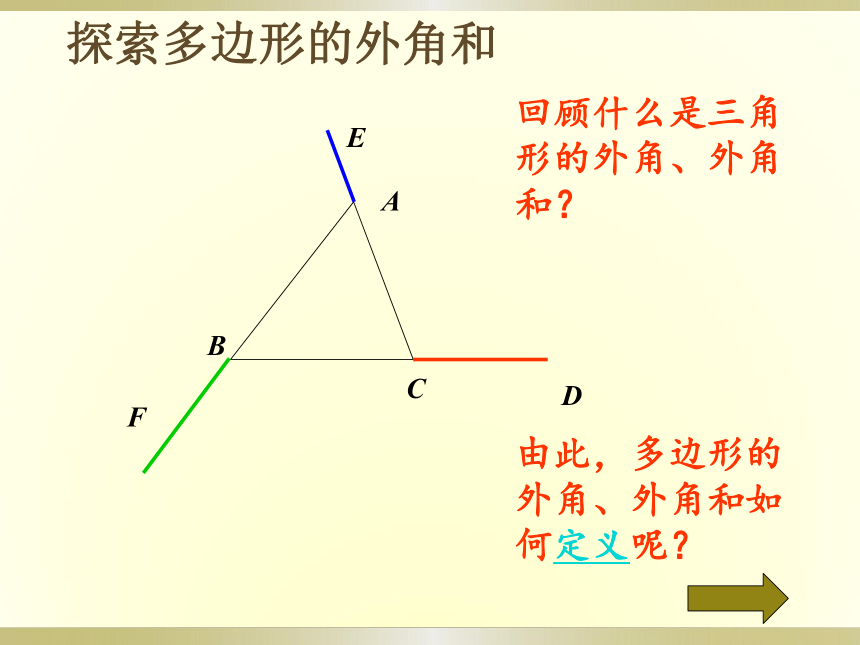
回顾什么是三角形的外角、外角和?
由此,多边形的外角、外角和如何定义呢?
A
B
C
D
E
F
探索多边形的外角和
多边形的外角与外角和
多边形内角的一边与________________所组成的角叫做这个多边形的外角。
与每个多边形的内角相邻的外角分别有____,他们是______ ,从与每个内角____________分别_______相加,所得的和即是多边形的__________。
探索新知
另一边的反向延长线
外角和
两个
对顶角
相邻的两个外角中
取一个
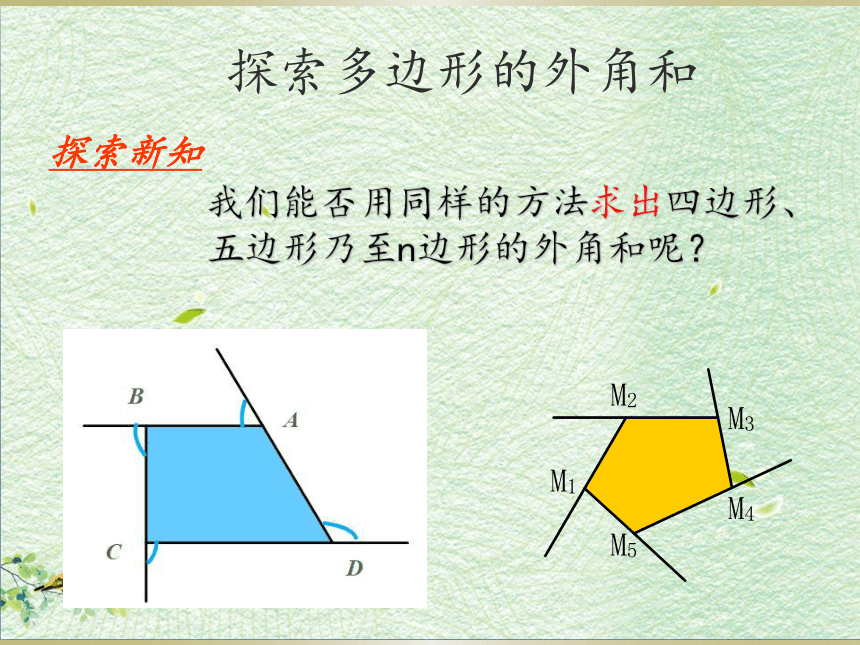
探索多边形的外角和
?????
探索新知
我们能否用同样的方法求出四边形、五边形乃至n边形的外角和呢?
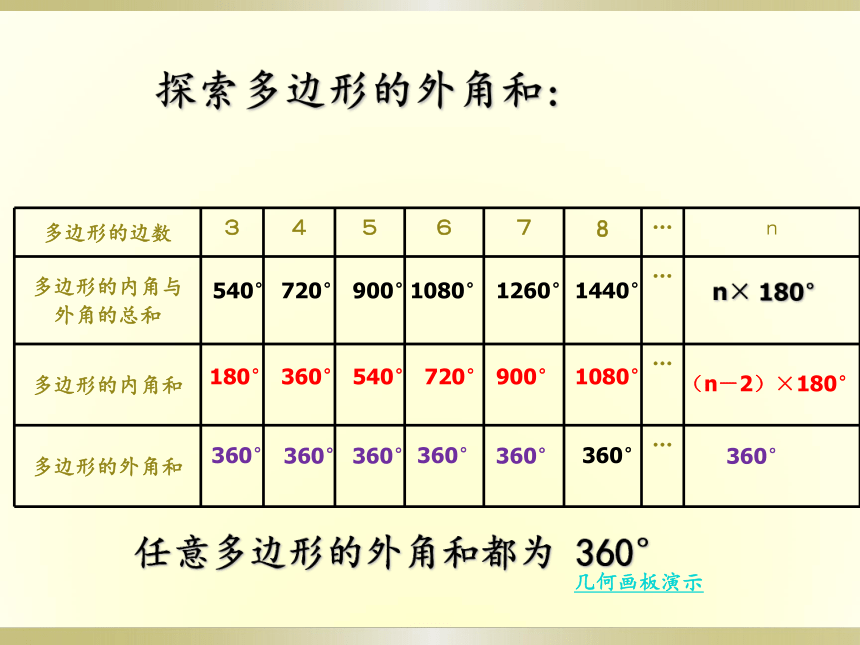
探索多边形的外角和:
任意多边形的外角和都为 360°
多边形的边数
3
4
5
6
7
8
…
n
多边形的内角与外角的总和
…
多边形的内角和
…
多边形的外角和
…
540°
720°
900°
1080°
1260°
180°
360°
540°
720°
900°
360°
360°
360°
360°
360°
n× 180°
(n-2)×180°
360°
几何画板演示
1440°
1080°
360°
例1:一个正多边形的一个内角为150°,
你知道它是几边形吗?
另解:
设这个多边形为n边形,根据题意得
(n-2)×180=150 n
n=12
答:这个多边形是
十二边形。
巩固提高
解:
由于多边形外角和等于360°
而这个正多边形的每个外角都等于
180°-150°=30°,
所以这个正多边形的边数等于
360°÷30°=12。
例2:多边形的每个外角都是相邻内角的 1/3 ,则此多边形是几边形?内角和、外角和分别是多少?
解:设一个外角为x°,则内角为3x°
根据题意得:
x+3x=180
x=45
360÷45=8
(8-2) ×180=1080
答:这个正多边形为正八边形,内角和为1080°,外角和为360°.
巩固提高
1、有一个正多边形的外角是60°,那么该正多边形是正________边形。
快速反应
2、有一个多边形的内角和是它的外角和的3倍,那么该多边形的边数是_______.
六
8
3、如图
∠M1+∠M2+∠M3 + ……+∠M6=_______。
???????
快速反应
360°
4、求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的值
A
B
E
D
F
C
G
H
快速反应
还有其他方法可以证明
多边形的外角和吗?
拓展延伸
方法2:探索五边形的外角和
∠1
∠2
∠3
∠5
∠4
360°
360°
F
试一试
我能行!!!
课堂小结
请同学们畅所欲言,
谈谈本节课的收获与感想。
作业
必做题:
同步练习册:
64页第3、8、9、12题
选做题:
尝试在 五边形 内部 做 两条平行线
来证明外角和为360°。
再见
第二课时
华东师大版七年级(下册)
多边形的外角和
9.2多边形的内角和与外角
第二课时
华东师大版七年级(下册)
多边形的外角和
温故知新
一、n 边形的内角和为__________
二、求七边形的内角和的度数.
(n-2) 180 °
解:(n-2)×180°
=(7-2)×180°
=900°
回顾什么是三角形的外角、外角和?
由此,多边形的外角、外角和如何定义呢?
A
B
C
D
E
F
探索多边形的外角和
多边形的外角与外角和
多边形内角的一边与________________所组成的角叫做这个多边形的外角。
与每个多边形的内角相邻的外角分别有____,他们是______ ,从与每个内角____________分别_______相加,所得的和即是多边形的__________。
探索新知
另一边的反向延长线
外角和
两个
对顶角
相邻的两个外角中
取一个
探索多边形的外角和
?????
探索新知
我们能否用同样的方法求出四边形、五边形乃至n边形的外角和呢?
探索多边形的外角和:
任意多边形的外角和都为 360°
多边形的边数
3
4
5
6
7
8
…
n
多边形的内角与外角的总和
…
多边形的内角和
…
多边形的外角和
…
540°
720°
900°
1080°
1260°
180°
360°
540°
720°
900°
360°
360°
360°
360°
360°
n× 180°
(n-2)×180°
360°
几何画板演示
1440°
1080°
360°
例1:一个正多边形的一个内角为150°,
你知道它是几边形吗?
另解:
设这个多边形为n边形,根据题意得
(n-2)×180=150 n
n=12
答:这个多边形是
十二边形。
巩固提高
解:
由于多边形外角和等于360°
而这个正多边形的每个外角都等于
180°-150°=30°,
所以这个正多边形的边数等于
360°÷30°=12。
例2:多边形的每个外角都是相邻内角的 1/3 ,则此多边形是几边形?内角和、外角和分别是多少?
解:设一个外角为x°,则内角为3x°
根据题意得:
x+3x=180
x=45
360÷45=8
(8-2) ×180=1080
答:这个正多边形为正八边形,内角和为1080°,外角和为360°.
巩固提高
1、有一个正多边形的外角是60°,那么该正多边形是正________边形。
快速反应
2、有一个多边形的内角和是它的外角和的3倍,那么该多边形的边数是_______.
六
8
3、如图
∠M1+∠M2+∠M3 + ……+∠M6=_______。
???????
快速反应
360°
4、求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的值
A
B
E
D
F
C
G
H
快速反应
还有其他方法可以证明
多边形的外角和吗?
拓展延伸
方法2:探索五边形的外角和
∠1
∠2
∠3
∠5
∠4
360°
360°
F
试一试
我能行!!!
课堂小结
请同学们畅所欲言,
谈谈本节课的收获与感想。
作业
必做题:
同步练习册:
64页第3、8、9、12题
选做题:
尝试在 五边形 内部 做 两条平行线
来证明外角和为360°。
再见
