华东师大版七年级下册数学:第8章 一元一次不等式复习(共19张ppt)
文档属性
| 名称 | 华东师大版七年级下册数学:第8章 一元一次不等式复习(共19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 21:29:45 | ||
图片预览





文档简介
华东师范大学版七年级数学下册
第 9 单元 多边形
第 8 课时 单元小结
知识回顾
三角形的三边关系
认识三角形
三角形的内角和与外角和
多边形的内角和与外角和
正多边形铺设地面
我们在《多边形》这一章中研究了哪些问题呢?
知识结构
三角形的三边关系
瓷砖的铺设
三 角 形
多 边 形
三角形的内角和
三角形的外角性质
三角形的外角和
多边形的内角和
多边形的外角和
用多边形铺满地面
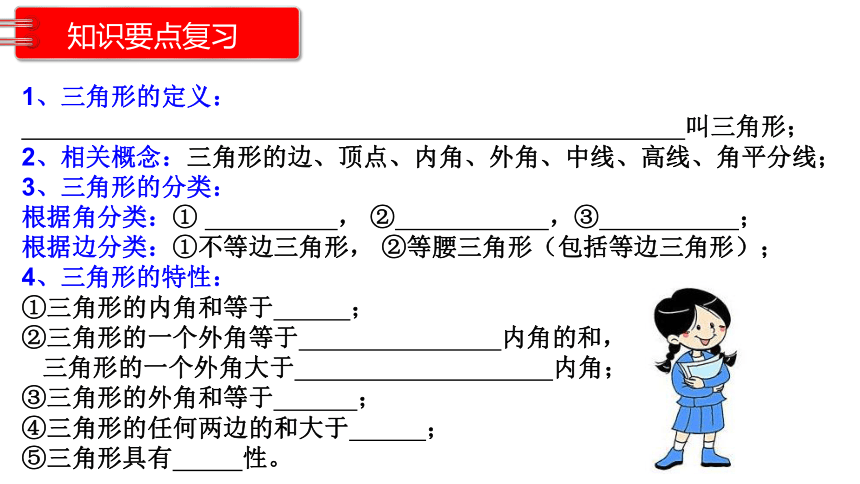
知识要点复习
1、三角形的定义:
叫三角形;
2、相关概念:三角形的边、顶点、内角、外角、中线、高线、角平分线;
3、三角形的分类:
根据角分类:① , ② ,③ ;
根据边分类:①不等边三角形, ②等腰三角形(包括等边三角形);
4、三角形的特性:
①三角形的内角和等于 ;
②三角形的一个外角等于 内角的和,
三角形的一个外角大于 内角;
③三角形的外角和等于 ;
④三角形的任何两边的和大于 ;
⑤三角形具有 性。
知识要点复习
1、三角形的定义:
叫三角形;
2、相关概念:三角形的边、顶点、内角、外角、中线、高线、角平分线;
3、三角形的分类:
根据角分类:① , ② ,③ ;
根据边分类:①不等边三角形, ②等腰三角形(包括等边三角形);
4、三角形的特性:
①三角形的内角和等于 ;
②三角形的一个外角等于 内角的和,
三角形的一个外角大于 内角;
③三角形的外角和等于 ;
④三角形的任何两边的和大于 ;
⑤三角形具有 性。
返回
180°
锐角三角形
直角三角形
钝角三角形
360°
第三边
稳定
不在同一条直线上的三条线段首尾顺次连接组成的平面图形
与他不相邻的两个
任何一个与它不相邻的
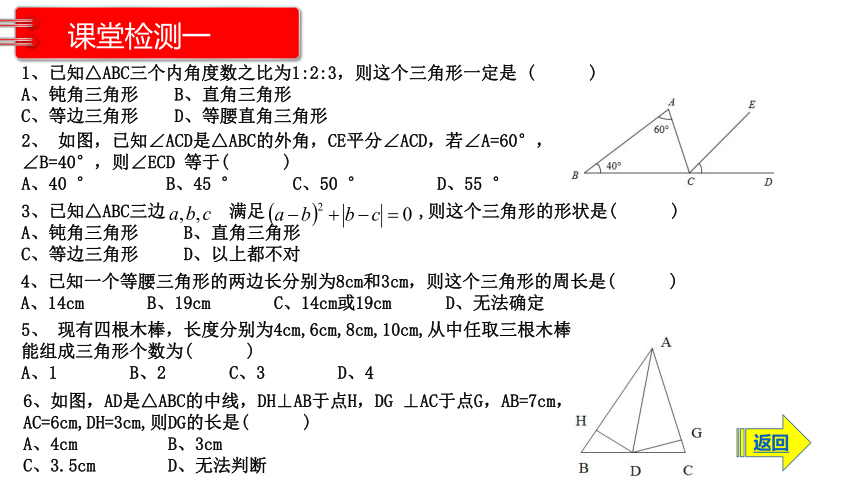
课堂检测一
1、已知△ABC三个内角度数之比为1:2:3,则这个三角形一定是 ( )
A、钝角三角形 B、直角三角形
C、等边三角形 D、等腰直角三角形
2、 如图,已知∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,
∠B=40°,则∠ECD 等于( )
A、40 ° B、45 ° C、50 ° D、55 °
3、已知△ABC三边 满足 ,则这个三角形的形状是( )
A、钝角三角形 B、直角三角形
C、等边三角形 D、以上都不对
4、已知一个等腰三角形的两边长分别为8cm和3cm,则这个三角形的周长是( )
A、14cm B、19cm C、14cm或19cm D、无法确定
5、 现有四根木棒,长度分别为4cm,6cm,8cm,10cm,从中任取三根木棒,
能组成三角形个数为( )
A、1 B、2 C、3 D、4
6、如图,AD是△ABC的中线,DH⊥AB于点H,DG ⊥AC于点G,AB=7cm,
AC=6cm,DH=3cm,则DG的长是( )
A、4cm B、3cm
C、3.5cm D、无法判断
返回
二元一次方程
知识点复习
1、n边形的定义:
叫n边形;
2、凸多边形、凹多边形、多边形的边、对角线;
3、正多边形: 叫正多边形;
4、多边形的特性:
①n边形的内角和为 ;
②任意多边形的外角和都为 ;
5、用正多边形铺设地面:
①用相同的正多边形;
②用多种正多边形 。
二元一次方程
知识点复习
1、n边形的定义:
叫n边形;
2、凸多边形、凹多边形、多边形的边、对角线;
3、正多边形: 叫正多边形;
4、多边形的特性:
①n边形的内角和为 ;
②任意多边形的外角和都为 ;
5、用正多边形铺设地面:
①用相同的正多边形;
②用多种正多边形 。
不在同一条直线上的n条线段首尾顺次连接组成的平面图形
各边相等,各内角也相等的多边形
(n-2)·180°
360°
类比思想
转化思想
课堂检测二
2、如图2,∠A+ ∠B+ ∠C +∠D +∠E +∠F +∠G的度数是( )
A、360° B、540° C、720° D、无法确定
1、如图1,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分 ∠EDC,∠BCD,
则∠P的度数是( )
A、50° B、55° C、60° D、65°
图1
图2
转化思想
4、用两种正多边形镶嵌,不能与正三角形匹配的正多边形是( )
A、正方形 B、正六边形 C、正十二边形 D、正十八边形
3、正三角形、正方形、正五边形、正六边形中不能单独镶嵌地面的是( )
A、正三角形 B、正方形 C、正五边形 D、正六边形
5、一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,
则原来多边形的边数是( )
A、10 B、11 C、12 D、以上都有可能
能力拓展
有一六边形,截去一三角形,内角和会发生怎样变化?请画图说明。并思考六边形的边数发生怎样的变化?
内角和减少1800
内角和不变
内角和增加1800
没过顶点
方法解析
返回
例:如图,在△ABC中,D是BC上一点,∠1=∠2,∠3=∠4,
∠BAC=63°求∠DAC的度数.
解:设∠1=x°
∵∠BAC=63°
∵∠3=∠4,则∠3=2x°
∵∠1=∠2,则∠2=x°
∴∠4=∠1+∠2=2x°
∵∠BAC+∠2+∠3=180°
∴ x+2x+63°=180°
∴ x=39°
∴ ∠DAC=∠BAC-∠1=63-39=24°
能力拓展
小结
方程思想
课时小结
通过这节课的复习,你有哪些收获!
老师小结
小结:322
三个数学思想:
两个基本方法:
类比思想,转化思想,方程思想;
添加辅助线,适当设未知数;
两个注意点:
①认真审题,找到正确的边角之间的数量关系;
②充分结合已学知识,学会将难度较大的问题分解成多个小问题来解决;
学习的敌人是自己的满足,要认真学习一点东西,必须从不自满开始。对自己,“学而不厌”,对人家,“诲人不倦”,我们应取这种态度。
—— 毛泽东
谢谢大家
重庆市江北中学 冯建刚
华东师范大学版七年级数学下册
第 9 单元 多边形
重庆市江北中学 冯建刚
第 8 课时 单元小结
返回
返回
返回
第 9 单元 多边形
第 8 课时 单元小结
知识回顾
三角形的三边关系
认识三角形
三角形的内角和与外角和
多边形的内角和与外角和
正多边形铺设地面
我们在《多边形》这一章中研究了哪些问题呢?
知识结构
三角形的三边关系
瓷砖的铺设
三 角 形
多 边 形
三角形的内角和
三角形的外角性质
三角形的外角和
多边形的内角和
多边形的外角和
用多边形铺满地面
知识要点复习
1、三角形的定义:
叫三角形;
2、相关概念:三角形的边、顶点、内角、外角、中线、高线、角平分线;
3、三角形的分类:
根据角分类:① , ② ,③ ;
根据边分类:①不等边三角形, ②等腰三角形(包括等边三角形);
4、三角形的特性:
①三角形的内角和等于 ;
②三角形的一个外角等于 内角的和,
三角形的一个外角大于 内角;
③三角形的外角和等于 ;
④三角形的任何两边的和大于 ;
⑤三角形具有 性。
知识要点复习
1、三角形的定义:
叫三角形;
2、相关概念:三角形的边、顶点、内角、外角、中线、高线、角平分线;
3、三角形的分类:
根据角分类:① , ② ,③ ;
根据边分类:①不等边三角形, ②等腰三角形(包括等边三角形);
4、三角形的特性:
①三角形的内角和等于 ;
②三角形的一个外角等于 内角的和,
三角形的一个外角大于 内角;
③三角形的外角和等于 ;
④三角形的任何两边的和大于 ;
⑤三角形具有 性。
返回
180°
锐角三角形
直角三角形
钝角三角形
360°
第三边
稳定
不在同一条直线上的三条线段首尾顺次连接组成的平面图形
与他不相邻的两个
任何一个与它不相邻的
课堂检测一
1、已知△ABC三个内角度数之比为1:2:3,则这个三角形一定是 ( )
A、钝角三角形 B、直角三角形
C、等边三角形 D、等腰直角三角形
2、 如图,已知∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,
∠B=40°,则∠ECD 等于( )
A、40 ° B、45 ° C、50 ° D、55 °
3、已知△ABC三边 满足 ,则这个三角形的形状是( )
A、钝角三角形 B、直角三角形
C、等边三角形 D、以上都不对
4、已知一个等腰三角形的两边长分别为8cm和3cm,则这个三角形的周长是( )
A、14cm B、19cm C、14cm或19cm D、无法确定
5、 现有四根木棒,长度分别为4cm,6cm,8cm,10cm,从中任取三根木棒,
能组成三角形个数为( )
A、1 B、2 C、3 D、4
6、如图,AD是△ABC的中线,DH⊥AB于点H,DG ⊥AC于点G,AB=7cm,
AC=6cm,DH=3cm,则DG的长是( )
A、4cm B、3cm
C、3.5cm D、无法判断
返回
二元一次方程
知识点复习
1、n边形的定义:
叫n边形;
2、凸多边形、凹多边形、多边形的边、对角线;
3、正多边形: 叫正多边形;
4、多边形的特性:
①n边形的内角和为 ;
②任意多边形的外角和都为 ;
5、用正多边形铺设地面:
①用相同的正多边形;
②用多种正多边形 。
二元一次方程
知识点复习
1、n边形的定义:
叫n边形;
2、凸多边形、凹多边形、多边形的边、对角线;
3、正多边形: 叫正多边形;
4、多边形的特性:
①n边形的内角和为 ;
②任意多边形的外角和都为 ;
5、用正多边形铺设地面:
①用相同的正多边形;
②用多种正多边形 。
不在同一条直线上的n条线段首尾顺次连接组成的平面图形
各边相等,各内角也相等的多边形
(n-2)·180°
360°
类比思想
转化思想
课堂检测二
2、如图2,∠A+ ∠B+ ∠C +∠D +∠E +∠F +∠G的度数是( )
A、360° B、540° C、720° D、无法确定
1、如图1,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分 ∠EDC,∠BCD,
则∠P的度数是( )
A、50° B、55° C、60° D、65°
图1
图2
转化思想
4、用两种正多边形镶嵌,不能与正三角形匹配的正多边形是( )
A、正方形 B、正六边形 C、正十二边形 D、正十八边形
3、正三角形、正方形、正五边形、正六边形中不能单独镶嵌地面的是( )
A、正三角形 B、正方形 C、正五边形 D、正六边形
5、一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,
则原来多边形的边数是( )
A、10 B、11 C、12 D、以上都有可能
能力拓展
有一六边形,截去一三角形,内角和会发生怎样变化?请画图说明。并思考六边形的边数发生怎样的变化?
内角和减少1800
内角和不变
内角和增加1800
没过顶点
方法解析
返回
例:如图,在△ABC中,D是BC上一点,∠1=∠2,∠3=∠4,
∠BAC=63°求∠DAC的度数.
解:设∠1=x°
∵∠BAC=63°
∵∠3=∠4,则∠3=2x°
∵∠1=∠2,则∠2=x°
∴∠4=∠1+∠2=2x°
∵∠BAC+∠2+∠3=180°
∴ x+2x+63°=180°
∴ x=39°
∴ ∠DAC=∠BAC-∠1=63-39=24°
能力拓展
小结
方程思想
课时小结
通过这节课的复习,你有哪些收获!
老师小结
小结:322
三个数学思想:
两个基本方法:
类比思想,转化思想,方程思想;
添加辅助线,适当设未知数;
两个注意点:
①认真审题,找到正确的边角之间的数量关系;
②充分结合已学知识,学会将难度较大的问题分解成多个小问题来解决;
学习的敌人是自己的满足,要认真学习一点东西,必须从不自满开始。对自己,“学而不厌”,对人家,“诲人不倦”,我们应取这种态度。
—— 毛泽东
谢谢大家
重庆市江北中学 冯建刚
华东师范大学版七年级数学下册
第 9 单元 多边形
重庆市江北中学 冯建刚
第 8 课时 单元小结
返回
返回
返回
