华东师大版数学八年级下册第19章 矩形、菱形与正方形 单元复习课件(共25张PPT)
文档属性
| 名称 | 华东师大版数学八年级下册第19章 矩形、菱形与正方形 单元复习课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 589.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 12:55:46 | ||
图片预览




文档简介
第19章 矩形、菱形与正方形
知识结构
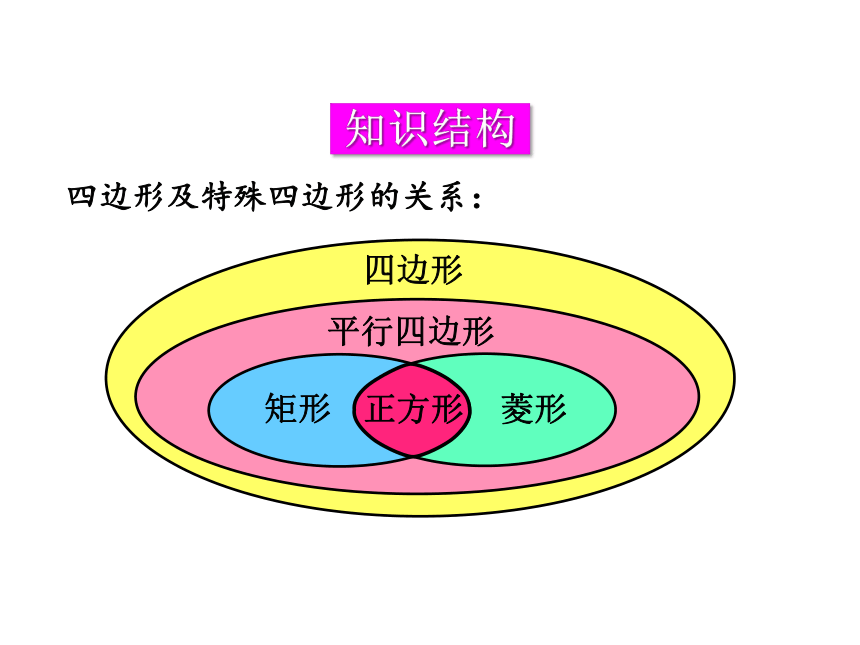
矩形
菱形
正方形
平行四边形
四边形
四边形及特殊四边形的关系:
平行四
边形
矩形
菱形
正方形
四边形
a
b
c
d
e
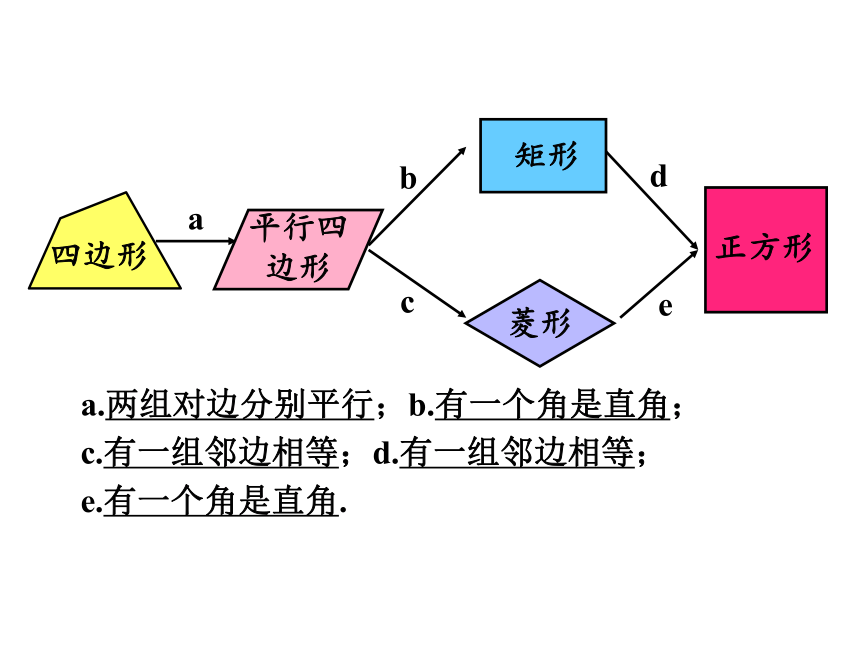
a.两组对边分别平行;b.有一个角是直角;
c.有一组邻边相等;d.有一组邻边相等;
e.有一个角是直角.
知识回顾
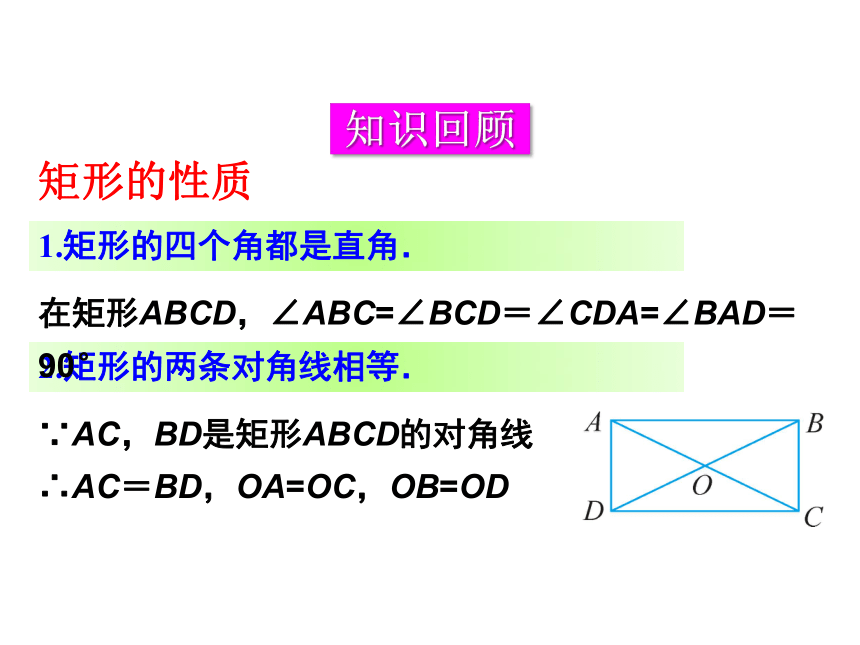
矩形的性质
在矩形ABCD,∠ABC=∠BCD=∠CDA=∠BAD=90°
∵AC,BD是矩形ABCD的对角线
∴AC=BD,OA=OC,OB=OD
矩形的判定
1.有一个角是直角的平行四边形是矩形.
2.对角线相等的平行四边形是矩形.
3.有三个角是直角的四边形是矩形.
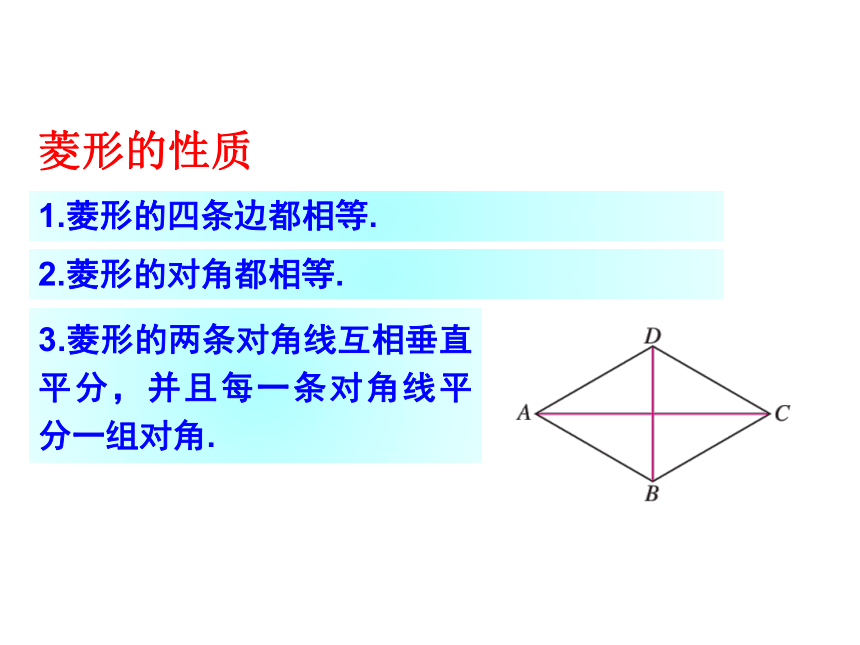
菱形的性质
菱形的判定
3.四条边都相等的四边形是菱形.
2.对角线互相垂直的平行四边形是菱形.
1.有一组邻边相等的平行四边形叫做菱形.
正方形的性质
正方形的判定
1.有一组邻边相等的矩形是正方形.
2.有一个角为直角的菱形是正方形.
典例精析
例1. 如图,E、F是平行四边形ABCD对角线BD上的两点,给出下列三个条件:
①BE=DF;②∠AEB=∠DFC;③AF∥EC.
请你从中选择一个适当的条件____,使四边形AECF是平行四边形.
①
例2. 如图,周长为68的矩形ABCD被分成7个大小完全一样的小矩形,则矩形ABCD的面积为( )
A.98 B.196 C.280 D.248
C
分析:设小长方形的长、宽分别为x、y,根据周长为68的矩形ABCD,可以列出方程4x+7y=68;根据图示可以列出方程2x=5y,联立两个方程组成方程组,解方程组就可以求出矩形ABCD的面积.
例3.如图,矩形ABCD的对角线AC、BD相交于点O,AP∥BD,DP∥AC,AP、DP相交于点P,则四边形AODP是什么样的特殊四边形,并说明你的理由.
分析:由AP∥BD,DP∥AC先判断四边形AODP是平行四边形,再由AO=DO判断四边形AODP为菱形.
解:四边形AODP是菱形,理由如下:
∵AP∥BD,DP∥AC,
∴四边形AODP是平行四边形
又∵矩形的对角线互相平分且相等,
得AO=DO,
由菱形的判定得四边形AODP为菱形.
例4.如图所示,有两条笔直的公路BD和EF(宽度不计),从一块矩形的土地ABCD中穿过,已知EF是BD的垂直平分线,BD=40米,EF=30米,求四边形BEDF的面积.
分析:连结DE、BF,因为四边形ABCD是矩形,所以AB∥CD,进而求证DF=BE,再求证FD=FB,即可判定四边形BFDE是菱形,根据菱形面积计算公式即可计算菱形BFDE的面积.
解:如图,连接DE、BF,∵四边形ABCD是矩形,
∴AB∥CD,∴∠ODF=∠OBE,
由EF垂直平分BD,
得OD=OB,∠DOF=∠BOE=90°,
∴△DOF≌△BOE,故DF=BE,
∴四边形BEDF是平行四边形,又∵EF是BD的垂直平分线,∴四边形BFDE是菱形,
∴
例5.如图,是一块在电脑屏幕上出现的矩形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形边长为1,求这个矩形色块图的面积.
分析:因为矩形内都是正方形,正方形的各边长相等,又有中间小正方形的边长为1,可利用边长之间的关系建立等式.
解:DF-AE=1,AE=BE+1,2CF-DF=1
DF=AE+1,AE=CF+1+1,DF=CF+3,
2CF-CF-3=1,解得CF=4,
∴BE=5,AE=6,
∴AB=11,BC=13
S=AB×BC=11×13=143.
随堂练习
1.矩形的两条对角线的夹角为60°,一条对角线与短边的和为15cm,则短边的边长为_____cm.
2.已知:如图,在矩形ABCD中,CE⊥BD,E为垂足,∠DCE:∠ECB=3:1,则∠ACE=_____度.
5
45
3.如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,则∠E=_____度.
22.5
4.如图,以△ABC的三边为边,在BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题,并说明理由.
(1)四边形ADEF是什么四边形;
(2)当△ABC满足什么条件时,四边形ADEF是矩形;
解:(1)四边形ADEF是平行四边形.
理由:∵△ABD,△EBC都是等边三角形.
∴AD=BD=AB,BC=BE=EC,∠DBA=∠EBC=60°
∴∠DBE+∠EBA=∠ABC+∠EBA.
∴∠DBE=∠ABC.在△DBE和△ABC中
∵BD=BA,∠DBE=∠ABC,BE=BC,
∴△DBE≌△ABC.∴DE=AC.
又∵△ACF是等边三角形,∴AC=AF.∴DE=AF.
同理可证:AD=EF,∴四边形ADEF是平行四边形.
(2)∵四边形ADEF是矩形,
∴∠FAD=90°.
∴∠BAC=360°-∠DAF-∠DAB-∠FAC=360°-90°-60°-60°=150°.
∴∠BAC=150°时,四边形ADEF是矩形.
课堂小结
谈谈你在这节课中,有什么收获?
知识结构
矩形
菱形
正方形
平行四边形
四边形
四边形及特殊四边形的关系:
平行四
边形
矩形
菱形
正方形
四边形
a
b
c
d
e
a.两组对边分别平行;b.有一个角是直角;
c.有一组邻边相等;d.有一组邻边相等;
e.有一个角是直角.
知识回顾
矩形的性质
在矩形ABCD,∠ABC=∠BCD=∠CDA=∠BAD=90°
∵AC,BD是矩形ABCD的对角线
∴AC=BD,OA=OC,OB=OD
矩形的判定
1.有一个角是直角的平行四边形是矩形.
2.对角线相等的平行四边形是矩形.
3.有三个角是直角的四边形是矩形.
菱形的性质
菱形的判定
3.四条边都相等的四边形是菱形.
2.对角线互相垂直的平行四边形是菱形.
1.有一组邻边相等的平行四边形叫做菱形.
正方形的性质
正方形的判定
1.有一组邻边相等的矩形是正方形.
2.有一个角为直角的菱形是正方形.
典例精析
例1. 如图,E、F是平行四边形ABCD对角线BD上的两点,给出下列三个条件:
①BE=DF;②∠AEB=∠DFC;③AF∥EC.
请你从中选择一个适当的条件____,使四边形AECF是平行四边形.
①
例2. 如图,周长为68的矩形ABCD被分成7个大小完全一样的小矩形,则矩形ABCD的面积为( )
A.98 B.196 C.280 D.248
C
分析:设小长方形的长、宽分别为x、y,根据周长为68的矩形ABCD,可以列出方程4x+7y=68;根据图示可以列出方程2x=5y,联立两个方程组成方程组,解方程组就可以求出矩形ABCD的面积.
例3.如图,矩形ABCD的对角线AC、BD相交于点O,AP∥BD,DP∥AC,AP、DP相交于点P,则四边形AODP是什么样的特殊四边形,并说明你的理由.
分析:由AP∥BD,DP∥AC先判断四边形AODP是平行四边形,再由AO=DO判断四边形AODP为菱形.
解:四边形AODP是菱形,理由如下:
∵AP∥BD,DP∥AC,
∴四边形AODP是平行四边形
又∵矩形的对角线互相平分且相等,
得AO=DO,
由菱形的判定得四边形AODP为菱形.
例4.如图所示,有两条笔直的公路BD和EF(宽度不计),从一块矩形的土地ABCD中穿过,已知EF是BD的垂直平分线,BD=40米,EF=30米,求四边形BEDF的面积.
分析:连结DE、BF,因为四边形ABCD是矩形,所以AB∥CD,进而求证DF=BE,再求证FD=FB,即可判定四边形BFDE是菱形,根据菱形面积计算公式即可计算菱形BFDE的面积.
解:如图,连接DE、BF,∵四边形ABCD是矩形,
∴AB∥CD,∴∠ODF=∠OBE,
由EF垂直平分BD,
得OD=OB,∠DOF=∠BOE=90°,
∴△DOF≌△BOE,故DF=BE,
∴四边形BEDF是平行四边形,又∵EF是BD的垂直平分线,∴四边形BFDE是菱形,
∴
例5.如图,是一块在电脑屏幕上出现的矩形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形边长为1,求这个矩形色块图的面积.
分析:因为矩形内都是正方形,正方形的各边长相等,又有中间小正方形的边长为1,可利用边长之间的关系建立等式.
解:DF-AE=1,AE=BE+1,2CF-DF=1
DF=AE+1,AE=CF+1+1,DF=CF+3,
2CF-CF-3=1,解得CF=4,
∴BE=5,AE=6,
∴AB=11,BC=13
S=AB×BC=11×13=143.
随堂练习
1.矩形的两条对角线的夹角为60°,一条对角线与短边的和为15cm,则短边的边长为_____cm.
2.已知:如图,在矩形ABCD中,CE⊥BD,E为垂足,∠DCE:∠ECB=3:1,则∠ACE=_____度.
5
45
3.如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,则∠E=_____度.
22.5
4.如图,以△ABC的三边为边,在BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题,并说明理由.
(1)四边形ADEF是什么四边形;
(2)当△ABC满足什么条件时,四边形ADEF是矩形;
解:(1)四边形ADEF是平行四边形.
理由:∵△ABD,△EBC都是等边三角形.
∴AD=BD=AB,BC=BE=EC,∠DBA=∠EBC=60°
∴∠DBE+∠EBA=∠ABC+∠EBA.
∴∠DBE=∠ABC.在△DBE和△ABC中
∵BD=BA,∠DBE=∠ABC,BE=BC,
∴△DBE≌△ABC.∴DE=AC.
又∵△ACF是等边三角形,∴AC=AF.∴DE=AF.
同理可证:AD=EF,∴四边形ADEF是平行四边形.
(2)∵四边形ADEF是矩形,
∴∠FAD=90°.
∴∠BAC=360°-∠DAF-∠DAB-∠FAC=360°-90°-60°-60°=150°.
∴∠BAC=150°时,四边形ADEF是矩形.
课堂小结
谈谈你在这节课中,有什么收获?
