华东师大版数学八年级下册课件:18.1.1 平行四边形的性质定理1、2(共29张PPT)
文档属性
| 名称 | 华东师大版数学八年级下册课件:18.1.1 平行四边形的性质定理1、2(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 00:00:00 | ||
图片预览



文档简介
第1课时 平行四边形的性质定理1、2
18.1 平行四边形的性质
新课导入
平行四边形是随处可见的几何图形
新课探索
回忆
我们知道,有两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
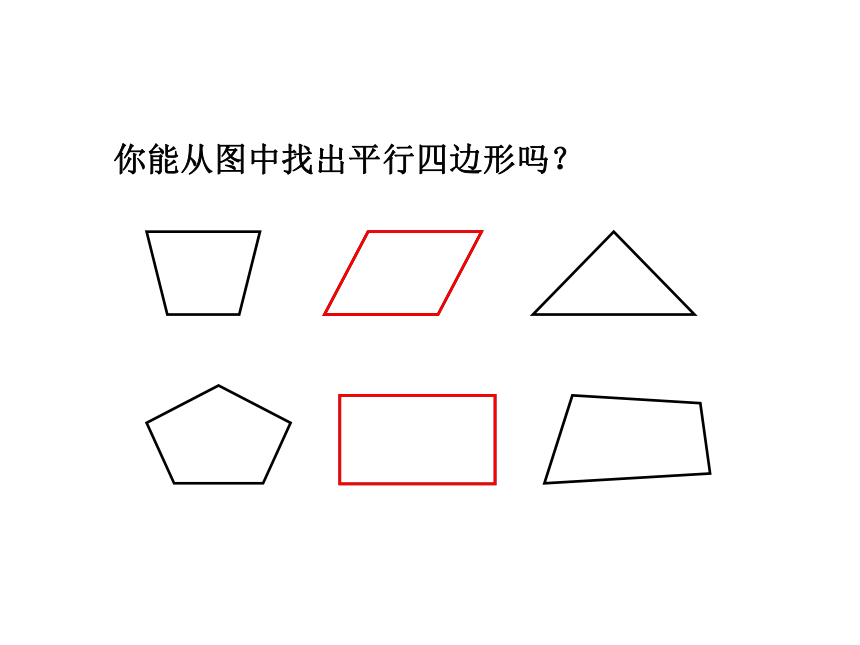
你能从图中找出平行四边形吗?
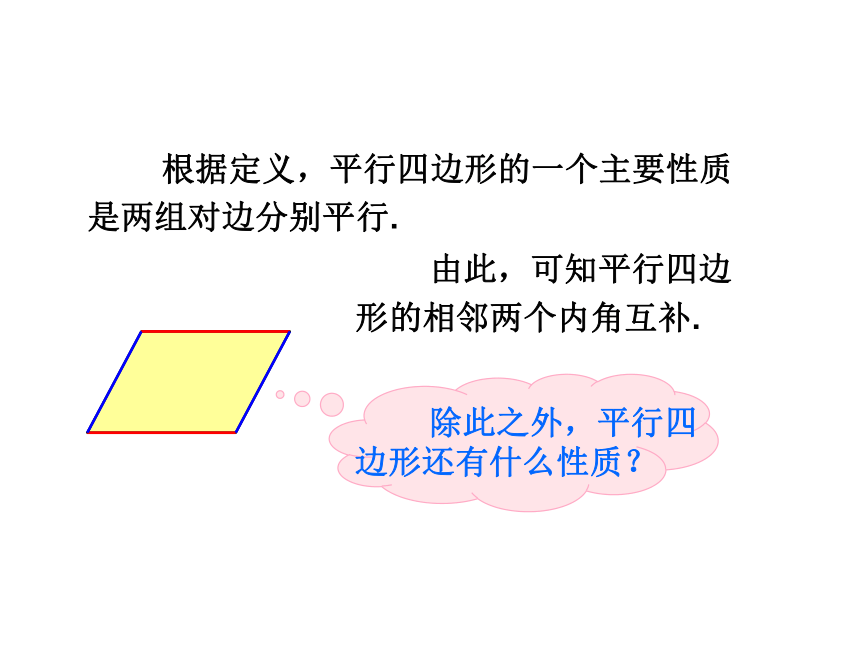
根据定义,平行四边形的一个主要性质是两组对边分别平行.
由此,可知平行四边形的相邻两个内角互补.
除此之外,平行四边形还有什么性质?
试
一
试
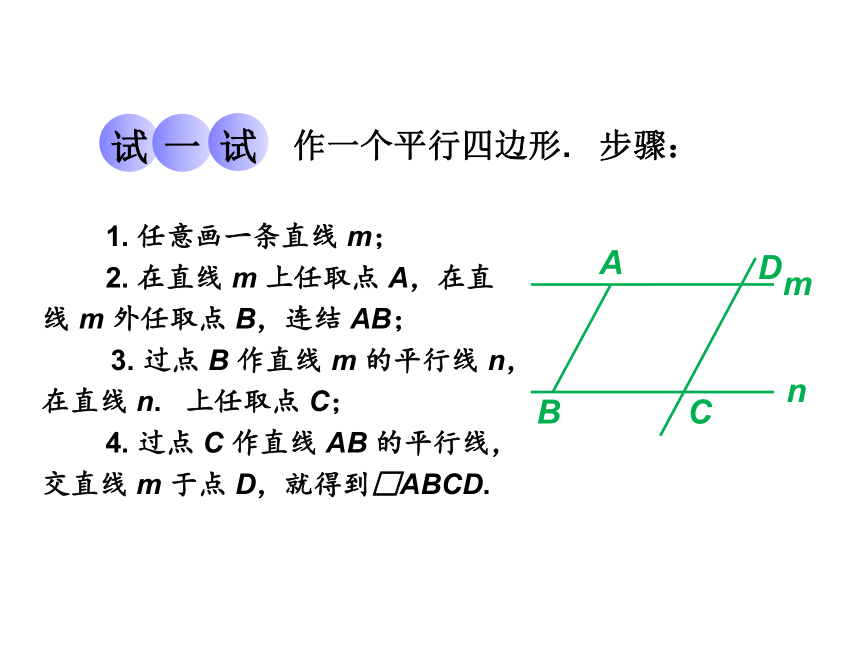
作一个平行四边形. 步骤:
1. 任意画一条直线 m;
2. 在直线 m 上任取点 A,在直线 m 外任取点 B,连结 AB;
3. 过点 B 作直线 m 的平行线 n,在直线 n. 上任取点 C;
4. 过点 C 作直线 AB 的平行线,交直线 m 于点 D,就得到□ABCD.
m
n
A
B
C
D
m
n
A
B
C
D
平行四边形 ABCD可以记作 ABCD .
探索
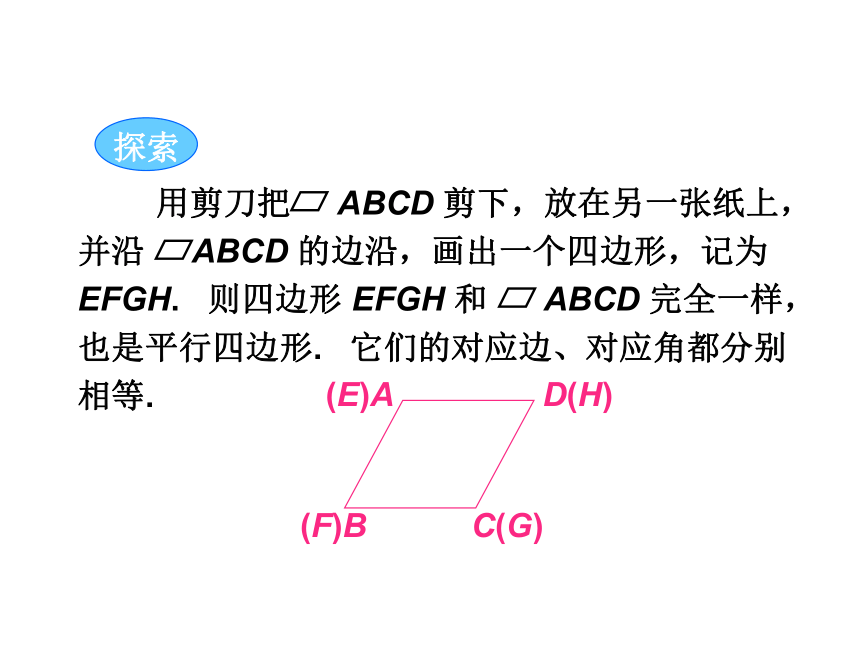
用剪刀把 ABCD 剪下,放在另一张纸上,并沿 ABCD 的边沿,画出一个四边形,记为 EFGH. 则四边形 EFGH 和 ABCD 完全一样,也是平行四边形. 它们的对应边、对应角都分别相等.
(E)A
(F)B
C(G)
D(H)
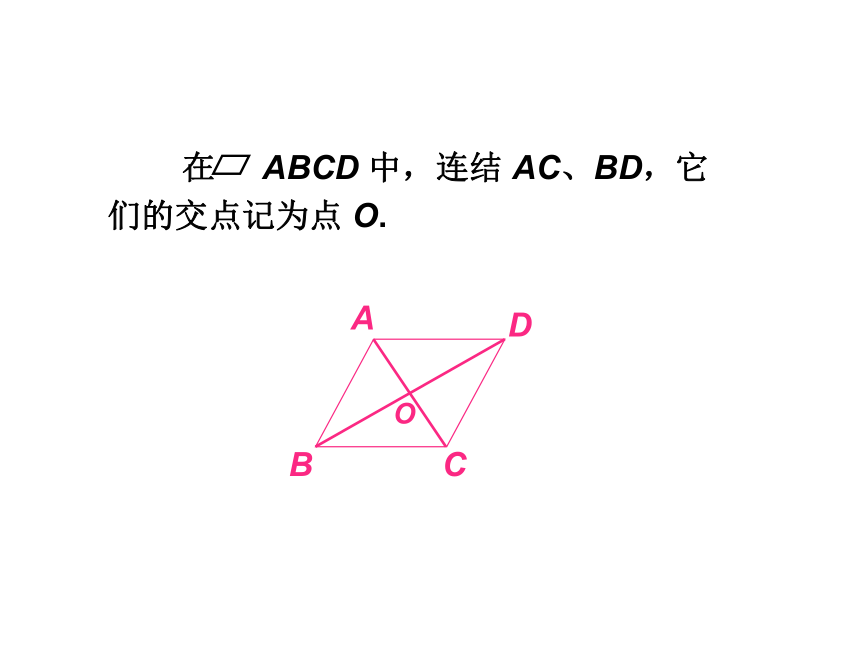
在 ABCD 中,连结 AC、BD,它们的交点记为点 O.
A
B
C
D
O
O
E
F
G
H
A
B
C
D
O
用一枚图钉穿过点 O,将 ABCD 绕点 O 旋转180°. 观察旋转后的 ABCD 和纸上所画的 EFGH 是否重合.
旋转 180°之后两个平行四边形完全重合.
平行四边形是中心对称图形,对角线的交点 O 就是对称中心.
AB = CD,AD = CB,
∠A =∠C,∠B =∠D.
已知:如图, ABCD.
求证:AB = CD,AD = CB,∠A =∠C,∠ABC =∠CDA.
A
B
C
D
证明 连结 BD.
∵ 四边形 ABCD 是平行四边形,
∴ AB // DC,AD // BC(平行四边形的两组对边分别平行),
∠ABD = ∠CDB ,∠ADB = ∠CBD.
又∵BD?=?DB,∴△ABD ≌ △CDB.
∴AB =?CD,AD?=?CB, ∠A = ∠C.
由 ∠ABD = ∠CDB 和 ∠ADB = ∠CBD.
得 ∠ABD + ∠CBD = ∠CDB + ∠ADB,
即 ∠ABC = ∠CDA.
平行四边形的性质定理:
平行四边形的性质定理 1 平行四边形的对边相等.
平行四边形的性质定理 2 平行四边形的对角相等.
例 1 如图,在 ABCD 中,∠A = 40°.求其他各内角的大小.
D
A
B
C
解 在 ABCD 中,
∠A =∠C,∠B =∠D(平行四边形的对角相等).
∵∠A = 40°,∴∠C = 40°.
又∵AD // BC,
∴∠A +∠B = 180°,
∴∠B = 180°– ∠A
= 180°– 40°= 140°,
∴∠D =∠B = 140°.
D
A
B
C
例 2 如图,在 ABCD 中,AB = 8,周长等于 24. 求其余三条边的长.
D
A
B
C
解?? 在 ABCD 中,
AB =?DC,AD =?BC(平行四边形的对边相等).
∵AB = 8,∴DC =?8.
又∵AB?+?BC +?DC + AD = 24,
∴AD = BC = (24 – 2AB)=?4.
1
2
D
A
B
C
练习
如图, ABCD 的周长是 28cm,△ABC 的周长是 22 cm,则 AC 的长为( )
A. 6 cm B. 12 cm C. 4 cm D. 8 cm
A
B
D
C
D
试
一
试
在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出平行线之间这些垂线段的长度.
这些线段都相等.
平行线的又一个性质:
平行线之间的距离处处相等.
两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离.
课堂小结
A
B
C
D
AB = CD,BC = AD;
∠A =∠C,∠B =∠D.
在 中:
ABCD
平行线之间的距离处处相等.
随堂演练
1. 如图,在 ABCD 中,AC = 4cm,CD= 3 cm,BC = 5 cm,则 ABCD 的面积为________.
A
D
C
B
4
5
3
12 cm2
2. 在 ABCD 中, ∠A 与∠B 的度数之比为 4∶5,∠A =_____, ∠B =_____, ∠C =_____,∠D =_____.
A
B
C
D
80°
100°
80°
100°
3. 平行四边形的一条角平分线分对边为 3 和4 两部分,求平行四边形的周长.
A
B
D
C
E
1
2
3
解:如图,∵ ABCD 中,
AD∥BC,∴∠1 =∠3,
又∠1 =∠2,∴∠2 =∠3,∴AB = BE.
当 BE = 3 时,AB = BE = 3,
∴ ABCD 的周长为:
(AB + BC)×2 =(3 + 7)×2 = 20.
当 BE = 4 时,AB = BE = 4,
∴ ABCD 的周长为:
(AB + BC)×2 =(4 + 7)×2 = 22.
A
B
D
C
E
1
2
3
4. 如图,在 中,已知 AD = 8 cm,AB = 6 cm,DE 平分∠ADC 交 BC 边于点 E,则BE 的长为________.
ABCD
2 cm
5. △ABC 是等腰三角形,AB = AC,P 是底边 BC 上一动点,PE∥AB,PF∥AC,点 E,F 分别在 AC,AB 上.求证:PE + PF = AB.
A
B
C
E
F
P
证明:∵ PE∥AB,PF∥AC ,
∴四边形 AEPF 为平行四边形,
∴PE = AF .
又 ∵PF ∥ AC,∴∠ FPB = ∠ C ,
∴ △BPF 为等腰三角形,
∴PF = FB,
∴ PE + PF
=AF + FB
=AB .
A
B
C
E
F
P
18.1 平行四边形的性质
新课导入
平行四边形是随处可见的几何图形
新课探索
回忆
我们知道,有两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
你能从图中找出平行四边形吗?
根据定义,平行四边形的一个主要性质是两组对边分别平行.
由此,可知平行四边形的相邻两个内角互补.
除此之外,平行四边形还有什么性质?
试
一
试
作一个平行四边形. 步骤:
1. 任意画一条直线 m;
2. 在直线 m 上任取点 A,在直线 m 外任取点 B,连结 AB;
3. 过点 B 作直线 m 的平行线 n,在直线 n. 上任取点 C;
4. 过点 C 作直线 AB 的平行线,交直线 m 于点 D,就得到□ABCD.
m
n
A
B
C
D
m
n
A
B
C
D
平行四边形 ABCD可以记作 ABCD .
探索
用剪刀把 ABCD 剪下,放在另一张纸上,并沿 ABCD 的边沿,画出一个四边形,记为 EFGH. 则四边形 EFGH 和 ABCD 完全一样,也是平行四边形. 它们的对应边、对应角都分别相等.
(E)A
(F)B
C(G)
D(H)
在 ABCD 中,连结 AC、BD,它们的交点记为点 O.
A
B
C
D
O
O
E
F
G
H
A
B
C
D
O
用一枚图钉穿过点 O,将 ABCD 绕点 O 旋转180°. 观察旋转后的 ABCD 和纸上所画的 EFGH 是否重合.
旋转 180°之后两个平行四边形完全重合.
平行四边形是中心对称图形,对角线的交点 O 就是对称中心.
AB = CD,AD = CB,
∠A =∠C,∠B =∠D.
已知:如图, ABCD.
求证:AB = CD,AD = CB,∠A =∠C,∠ABC =∠CDA.
A
B
C
D
证明 连结 BD.
∵ 四边形 ABCD 是平行四边形,
∴ AB // DC,AD // BC(平行四边形的两组对边分别平行),
∠ABD = ∠CDB ,∠ADB = ∠CBD.
又∵BD?=?DB,∴△ABD ≌ △CDB.
∴AB =?CD,AD?=?CB, ∠A = ∠C.
由 ∠ABD = ∠CDB 和 ∠ADB = ∠CBD.
得 ∠ABD + ∠CBD = ∠CDB + ∠ADB,
即 ∠ABC = ∠CDA.
平行四边形的性质定理:
平行四边形的性质定理 1 平行四边形的对边相等.
平行四边形的性质定理 2 平行四边形的对角相等.
例 1 如图,在 ABCD 中,∠A = 40°.求其他各内角的大小.
D
A
B
C
解 在 ABCD 中,
∠A =∠C,∠B =∠D(平行四边形的对角相等).
∵∠A = 40°,∴∠C = 40°.
又∵AD // BC,
∴∠A +∠B = 180°,
∴∠B = 180°– ∠A
= 180°– 40°= 140°,
∴∠D =∠B = 140°.
D
A
B
C
例 2 如图,在 ABCD 中,AB = 8,周长等于 24. 求其余三条边的长.
D
A
B
C
解?? 在 ABCD 中,
AB =?DC,AD =?BC(平行四边形的对边相等).
∵AB = 8,∴DC =?8.
又∵AB?+?BC +?DC + AD = 24,
∴AD = BC = (24 – 2AB)=?4.
1
2
D
A
B
C
练习
如图, ABCD 的周长是 28cm,△ABC 的周长是 22 cm,则 AC 的长为( )
A. 6 cm B. 12 cm C. 4 cm D. 8 cm
A
B
D
C
D
试
一
试
在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出平行线之间这些垂线段的长度.
这些线段都相等.
平行线的又一个性质:
平行线之间的距离处处相等.
两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离.
课堂小结
A
B
C
D
AB = CD,BC = AD;
∠A =∠C,∠B =∠D.
在 中:
ABCD
平行线之间的距离处处相等.
随堂演练
1. 如图,在 ABCD 中,AC = 4cm,CD= 3 cm,BC = 5 cm,则 ABCD 的面积为________.
A
D
C
B
4
5
3
12 cm2
2. 在 ABCD 中, ∠A 与∠B 的度数之比为 4∶5,∠A =_____, ∠B =_____, ∠C =_____,∠D =_____.
A
B
C
D
80°
100°
80°
100°
3. 平行四边形的一条角平分线分对边为 3 和4 两部分,求平行四边形的周长.
A
B
D
C
E
1
2
3
解:如图,∵ ABCD 中,
AD∥BC,∴∠1 =∠3,
又∠1 =∠2,∴∠2 =∠3,∴AB = BE.
当 BE = 3 时,AB = BE = 3,
∴ ABCD 的周长为:
(AB + BC)×2 =(3 + 7)×2 = 20.
当 BE = 4 时,AB = BE = 4,
∴ ABCD 的周长为:
(AB + BC)×2 =(4 + 7)×2 = 22.
A
B
D
C
E
1
2
3
4. 如图,在 中,已知 AD = 8 cm,AB = 6 cm,DE 平分∠ADC 交 BC 边于点 E,则BE 的长为________.
ABCD
2 cm
5. △ABC 是等腰三角形,AB = AC,P 是底边 BC 上一动点,PE∥AB,PF∥AC,点 E,F 分别在 AC,AB 上.求证:PE + PF = AB.
A
B
C
E
F
P
证明:∵ PE∥AB,PF∥AC ,
∴四边形 AEPF 为平行四边形,
∴PE = AF .
又 ∵PF ∥ AC,∴∠ FPB = ∠ C ,
∴ △BPF 为等腰三角形,
∴PF = FB,
∴ PE + PF
=AF + FB
=AB .
A
B
C
E
F
P
