华东师大版数学八年级下册课件:18.1.2平行四边形的性质1、2的综合运用(共20张PPT)
文档属性
| 名称 | 华东师大版数学八年级下册课件:18.1.2平行四边形的性质1、2的综合运用(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 337.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 13:35:20 | ||
图片预览


文档简介
第2课时 平行四边形的性质1、2的综合运用
新课导入
A
B
C
D
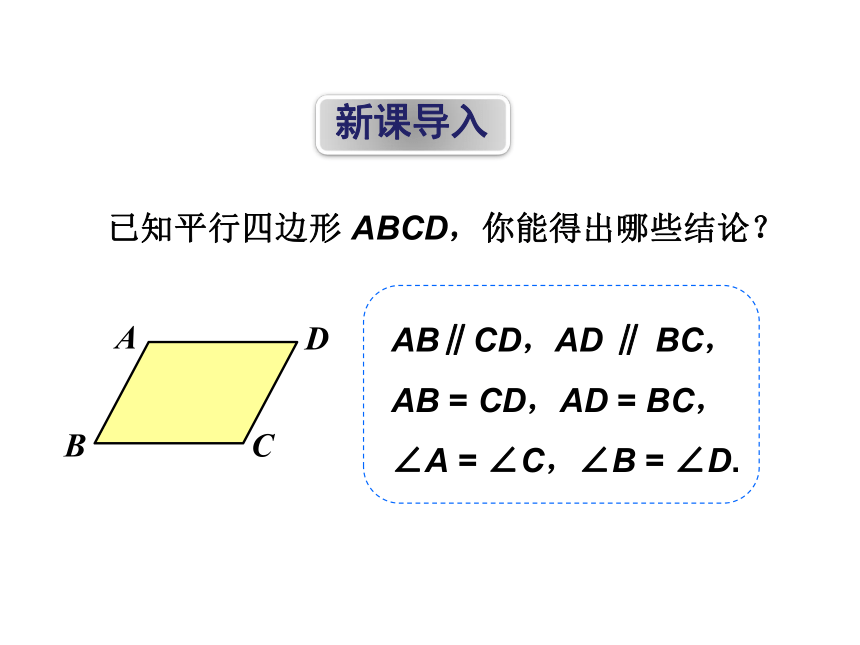
已知平行四边形 ABCD,你能得出哪些结论?
AB∥CD,AD ∥ BC,
AB = CD,AD = BC,
∠A = ∠C,∠B = ∠D.
新课探索
例 3 已知平行四边形的周长是 24,相邻两边的长度相差 4,求该平行四边形相邻两边的长.
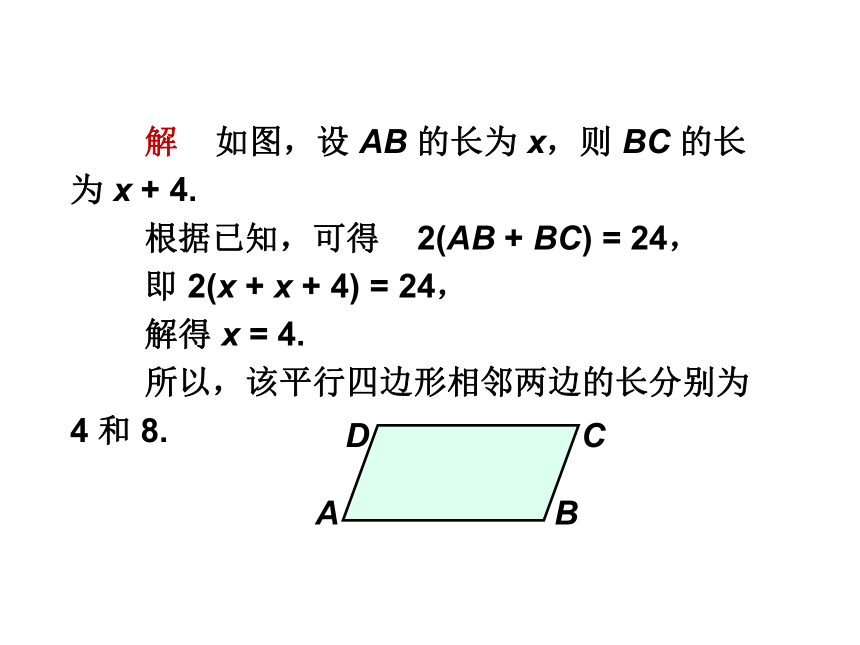
解 如图,设 AB 的长为 x,则 BC 的长为 x + 4.
根据已知,可得 2(AB + BC) = 24,
即 2(x + x + 4) = 24,
解得 x = 4.
所以,该平行四边形相邻两边的长分别为 4 和 8.
A
B
C
D
练习
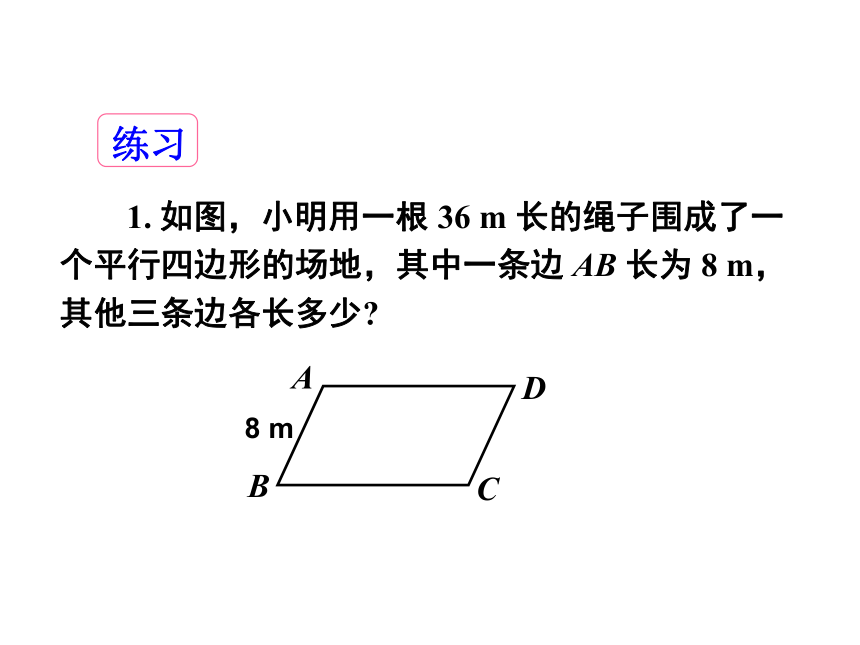
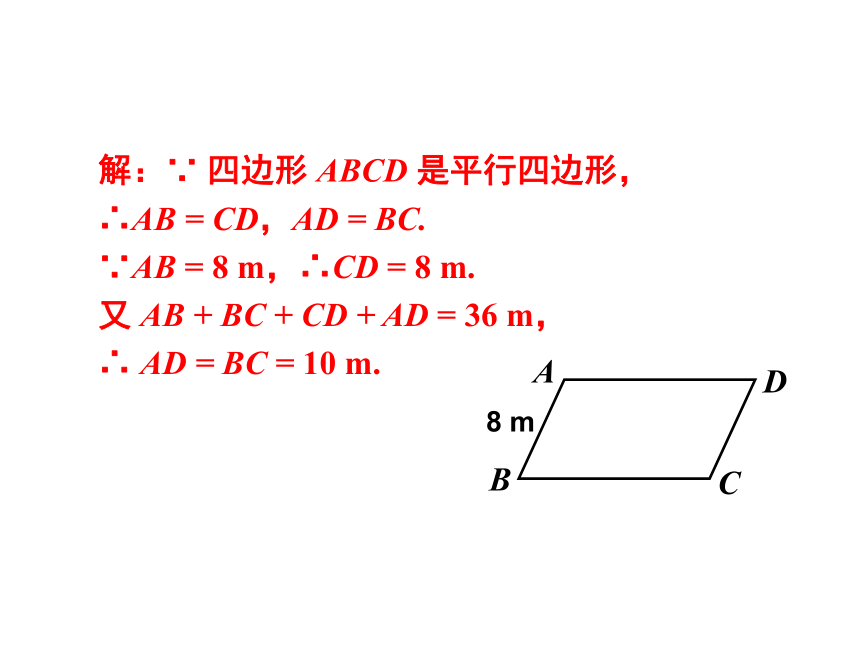
1. 如图,小明用一根 36 m 长的绳子围成了一个平行四边形的场地,其中一条边 AB 长为 8 m,其他三条边各长多少?
A
D
B
C
8 m
解:∵ 四边形 ABCD 是平行四边形,
∴AB = CD,AD = BC.
∵AB = 8 m,∴CD = 8 m.
又 AB + BC + CD + AD = 36 m,
∴ AD = BC = 10 m.
A
D
B
C
8 m
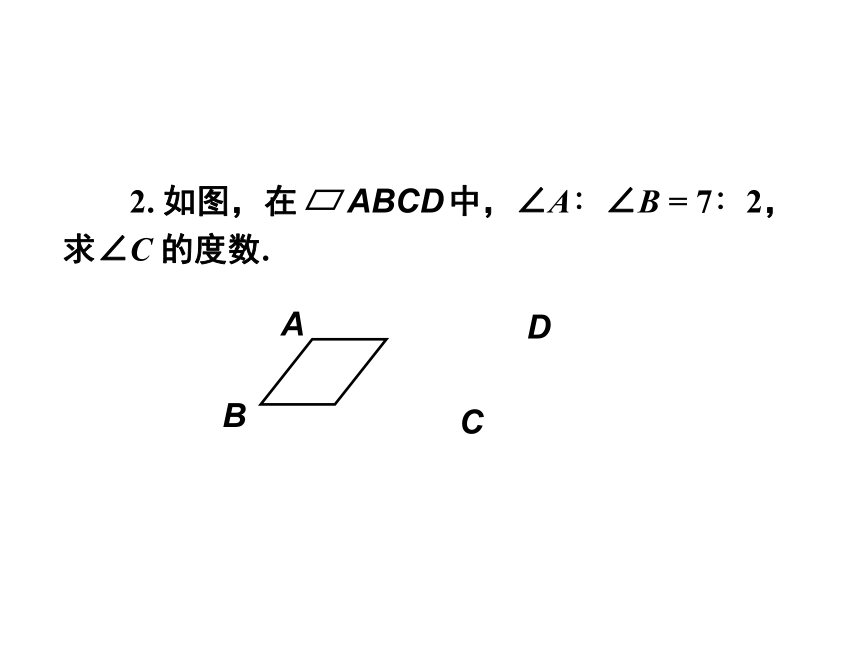
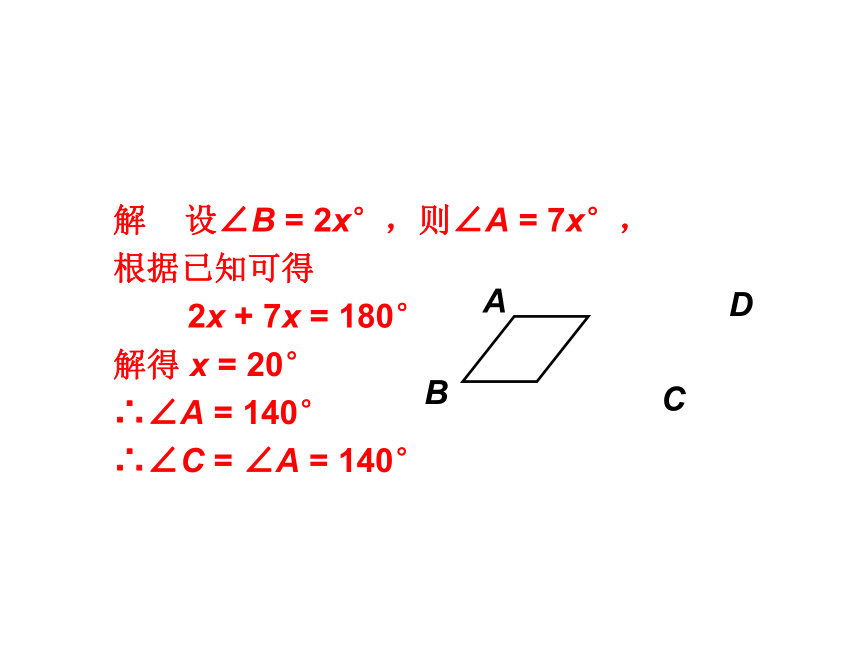
2. 如图,在 中,∠A∶∠B = 7∶2,求∠C 的度数.
ABCD
A
D
B
C
解 设∠B = 2x°,则∠A = 7x°,
根据已知可得
2x + 7x = 180°
解得 x = 20°
∴∠A = 140°
∴∠C = ∠A = 140°
A
D
B
C
3. 已知平行四边形的周长是32 cm,相邻两边的长相等,求该平行四边形各边的长.
解 32÷4 = 8(cm)
该平行四边形各边的长都是 8 cm.
例 4 已知:如图,在 ABCD 中,∠ADC 的平分线与 AB 相交于点 E. 求证: BE + BC = CD.
A
B
E
C
D
证明 ∵四边形 ABCD 是平行四边形,
∴AB = CD(平行四边形的对边相等),
AB∥CD (平行四边形的对边平行),
∴∠CDE =∠AED.
又∵DE 是∠ADC 的平分线,
∴∠ADE =∠CDE,
∴∠ADE =∠AED,∴AD = AE.
又∵AD = BC(平行四边形的对边相等),
∴AE = BC. BE + BC = BE + AE = AB = CD.
A
B
E
C
D
练习
如图,在 ABCD 中,AE 平分∠BAD,BE 平分∠ABC,且 AE、BE 相交于 CD 上的一点 E. 求证:AE⊥BE.
A
B
C
D
E
A
B
C
D
E
解 ∵四边形 ABCD 是平行四边形,
∴∠DAB + ∠ABC = 180°,
又因为AE 平分∠BAD,BE 平分∠ABC,
∴∠EAB = ∠DAB,∠EBA = ∠ABC,
∴∠EAB + ∠EBA = ×180°= 90°
∴ ∠AEB = 180°– 90°= 90°
∴AE⊥BE.
1
2
1
2
1
2
随堂演练
1. 在 中,∠A∶∠B = 2∶3,求各角的度数.
ABCD
解:∵四边形 ABCD 为平行四边形,
∴∠A +∠B = 180°,∠A =∠C,∠B =∠D.
又∵∠A∶∠B = 2∶3,
∴∠A =∠C = 72°,∠B =∠D = 108°.
2. 在 ABCD中,∠A∶∠B∶∠C ∶∠D的值可以是( )
A. 1∶2∶3∶4
B. 1∶2∶2∶1
C. 2∶2∶1∶1
D. 2∶1∶2∶1
D
3. 已知 的周长为 28 cm,AB∶BC = 3∶4,求它的各边的长.
ABCD
解:∵四边形 ABCD 为平行四边形,
∴AB = CD,AD = BC.
又∵C ABCD = AB + BC + CD + AD = 28 cm,
且 AB∶BC = 3∶4,
∴AB = CD = 6 cm,AD = BC = 8 cm.
4. 如果平行四边形的一组邻边的长相等,且等于其较短的对角线的长,而此对角线的长为 4 cm,求此平行四边形各内角的大小及各边的长.
解 由题意得,
AB = AD = CD = BC = BD = 4.
∴∠DAB =∠DCB = 60°,
∴∠ADC = ∠ABC = 120°.
A
B
C
D
5. 如图, ABCD 中,DE⊥AB,BF⊥CD,垂足分别为 E,F. 求证:AE = CF.
证明: ∵四边形 ABCD 是平行四边形,
∴ ∠A = ∠C,AD = CB.
又∠AED = ∠CFB = 90°,
∴ △ADE ≌ △CBF,
∴AE = CF.
变式:DE = BF 吗?
6. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了个四边形,转动其中一张纸条,线段 AD 和 BC 的长度有什么关系?为什么?
解:线段 AD = BC. 因为两张纸条的对边都平行,所以重合的部分构成的四边形是平行四边形,平行四边形的对边相等,所以 AD = BC.
新课导入
A
B
C
D
已知平行四边形 ABCD,你能得出哪些结论?
AB∥CD,AD ∥ BC,
AB = CD,AD = BC,
∠A = ∠C,∠B = ∠D.
新课探索
例 3 已知平行四边形的周长是 24,相邻两边的长度相差 4,求该平行四边形相邻两边的长.
解 如图,设 AB 的长为 x,则 BC 的长为 x + 4.
根据已知,可得 2(AB + BC) = 24,
即 2(x + x + 4) = 24,
解得 x = 4.
所以,该平行四边形相邻两边的长分别为 4 和 8.
A
B
C
D
练习
1. 如图,小明用一根 36 m 长的绳子围成了一个平行四边形的场地,其中一条边 AB 长为 8 m,其他三条边各长多少?
A
D
B
C
8 m
解:∵ 四边形 ABCD 是平行四边形,
∴AB = CD,AD = BC.
∵AB = 8 m,∴CD = 8 m.
又 AB + BC + CD + AD = 36 m,
∴ AD = BC = 10 m.
A
D
B
C
8 m
2. 如图,在 中,∠A∶∠B = 7∶2,求∠C 的度数.
ABCD
A
D
B
C
解 设∠B = 2x°,则∠A = 7x°,
根据已知可得
2x + 7x = 180°
解得 x = 20°
∴∠A = 140°
∴∠C = ∠A = 140°
A
D
B
C
3. 已知平行四边形的周长是32 cm,相邻两边的长相等,求该平行四边形各边的长.
解 32÷4 = 8(cm)
该平行四边形各边的长都是 8 cm.
例 4 已知:如图,在 ABCD 中,∠ADC 的平分线与 AB 相交于点 E. 求证: BE + BC = CD.
A
B
E
C
D
证明 ∵四边形 ABCD 是平行四边形,
∴AB = CD(平行四边形的对边相等),
AB∥CD (平行四边形的对边平行),
∴∠CDE =∠AED.
又∵DE 是∠ADC 的平分线,
∴∠ADE =∠CDE,
∴∠ADE =∠AED,∴AD = AE.
又∵AD = BC(平行四边形的对边相等),
∴AE = BC. BE + BC = BE + AE = AB = CD.
A
B
E
C
D
练习
如图,在 ABCD 中,AE 平分∠BAD,BE 平分∠ABC,且 AE、BE 相交于 CD 上的一点 E. 求证:AE⊥BE.
A
B
C
D
E
A
B
C
D
E
解 ∵四边形 ABCD 是平行四边形,
∴∠DAB + ∠ABC = 180°,
又因为AE 平分∠BAD,BE 平分∠ABC,
∴∠EAB = ∠DAB,∠EBA = ∠ABC,
∴∠EAB + ∠EBA = ×180°= 90°
∴ ∠AEB = 180°– 90°= 90°
∴AE⊥BE.
1
2
1
2
1
2
随堂演练
1. 在 中,∠A∶∠B = 2∶3,求各角的度数.
ABCD
解:∵四边形 ABCD 为平行四边形,
∴∠A +∠B = 180°,∠A =∠C,∠B =∠D.
又∵∠A∶∠B = 2∶3,
∴∠A =∠C = 72°,∠B =∠D = 108°.
2. 在 ABCD中,∠A∶∠B∶∠C ∶∠D的值可以是( )
A. 1∶2∶3∶4
B. 1∶2∶2∶1
C. 2∶2∶1∶1
D. 2∶1∶2∶1
D
3. 已知 的周长为 28 cm,AB∶BC = 3∶4,求它的各边的长.
ABCD
解:∵四边形 ABCD 为平行四边形,
∴AB = CD,AD = BC.
又∵C ABCD = AB + BC + CD + AD = 28 cm,
且 AB∶BC = 3∶4,
∴AB = CD = 6 cm,AD = BC = 8 cm.
4. 如果平行四边形的一组邻边的长相等,且等于其较短的对角线的长,而此对角线的长为 4 cm,求此平行四边形各内角的大小及各边的长.
解 由题意得,
AB = AD = CD = BC = BD = 4.
∴∠DAB =∠DCB = 60°,
∴∠ADC = ∠ABC = 120°.
A
B
C
D
5. 如图, ABCD 中,DE⊥AB,BF⊥CD,垂足分别为 E,F. 求证:AE = CF.
证明: ∵四边形 ABCD 是平行四边形,
∴ ∠A = ∠C,AD = CB.
又∠AED = ∠CFB = 90°,
∴ △ADE ≌ △CBF,
∴AE = CF.
变式:DE = BF 吗?
6. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了个四边形,转动其中一张纸条,线段 AD 和 BC 的长度有什么关系?为什么?
解:线段 AD = BC. 因为两张纸条的对边都平行,所以重合的部分构成的四边形是平行四边形,平行四边形的对边相等,所以 AD = BC.
