华东师大版数学八年级下册课件:18.1.4 平行四边形的性质定理3的综合运用(共22张PPT)
文档属性
| 名称 | 华东师大版数学八年级下册课件:18.1.4 平行四边形的性质定理3的综合运用(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 407.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 21:23:30 | ||
图片预览


文档简介
第4课时 平行四边形的性质定理 3的综合运用
新课导入
平行四边形有什么性质?
性质 1 平行四边形的对边相等
性质 2 平行四边形的对角相等
性质 3 平行四边形的对角线互相平分
新课探索
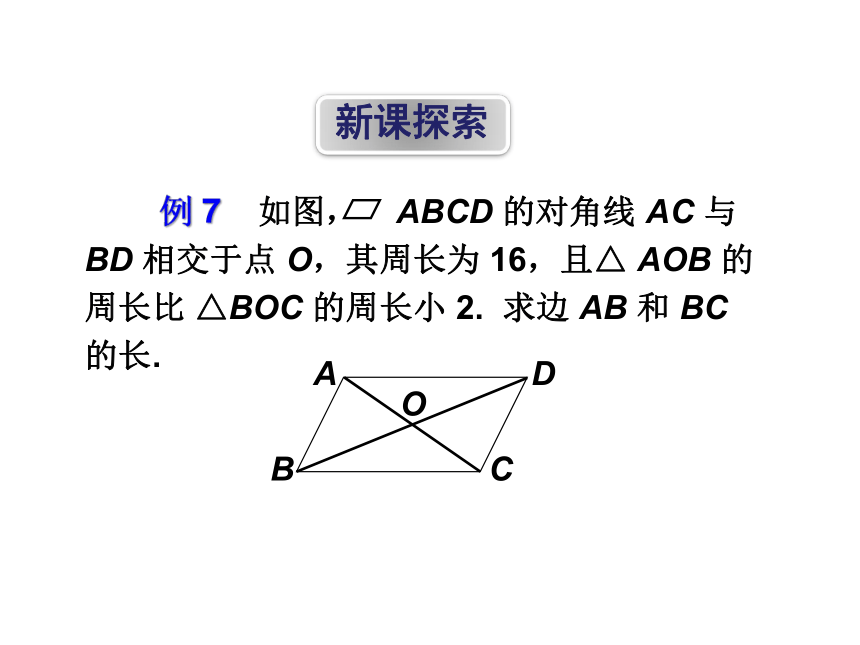
例 7? ?如图, ABCD 的对角线 AC 与 BD 相交于点 O,其周长为 16,且△ AOB 的周长比 △BOC 的周长小 2. 求边 AB 和 BC 的长.
A
B
C
D
O
A
B
C
D
O
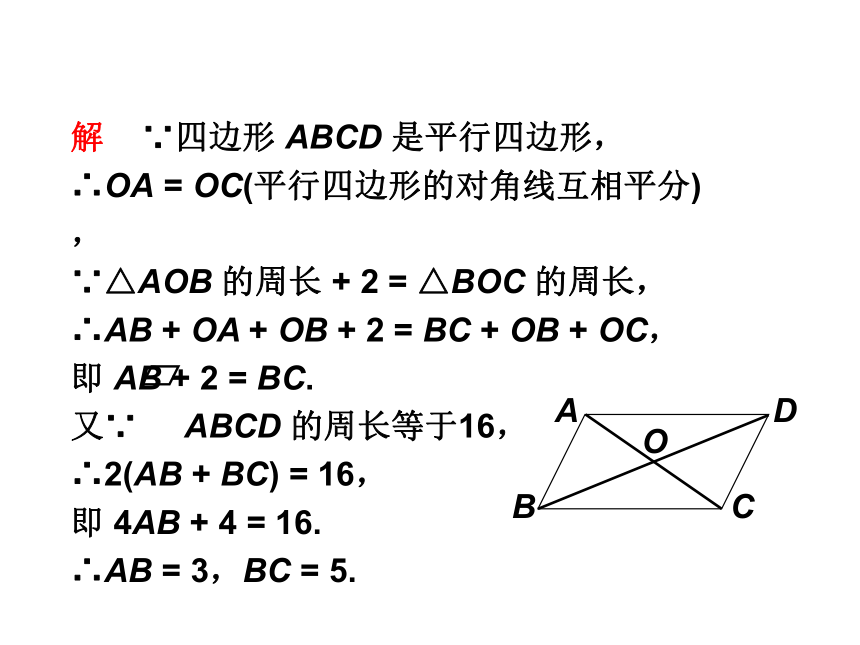
解 ∵四边形 ABCD 是平行四边形,
∴OA = OC(平行四边形的对角线互相平分),
∵△AOB 的周长 + 2 = △BOC 的周长,
∴AB + OA + OB + 2 = BC + OB + OC,
即 AB + 2 = BC.
又∵ ABCD 的周长等于16,
∴2(AB + BC) = 16,
即 4AB + 4 = 16.
∴AB = 3,BC = 5.
练习
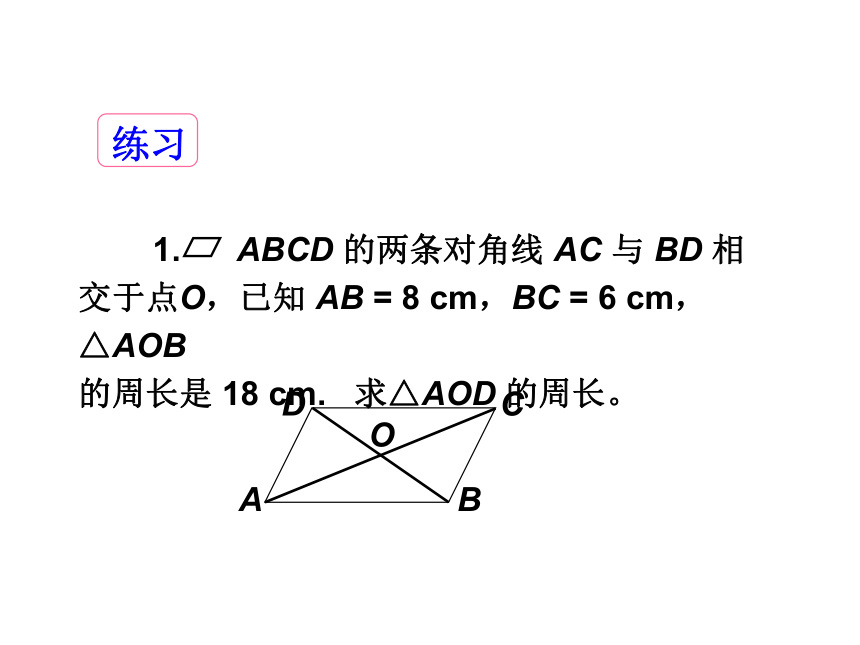
1. ABCD 的两条对角线 AC 与 BD 相交于点O,已知 AB = 8 cm,BC = 6 cm,△AOB
的周长是 18 cm. 求△AOD 的周长。
D
A
B
C
O
D
A
B
C
O
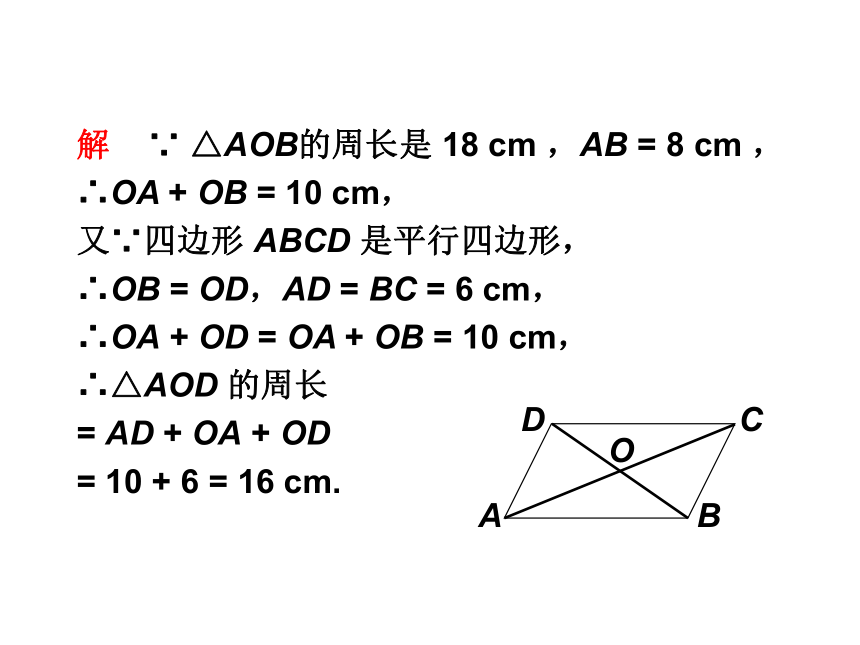
解 ∵ △AOB的周长是 18 cm ,AB = 8 cm ,
∴OA + OB = 10 cm,
又∵四边形 ABCD 是平行四边形,
∴OB = OD,AD = BC = 6 cm,
∴OA + OD = OA + OB = 10 cm,
∴△AOD 的周长
= AD + OA + OD
= 10 + 6 = 16 cm.
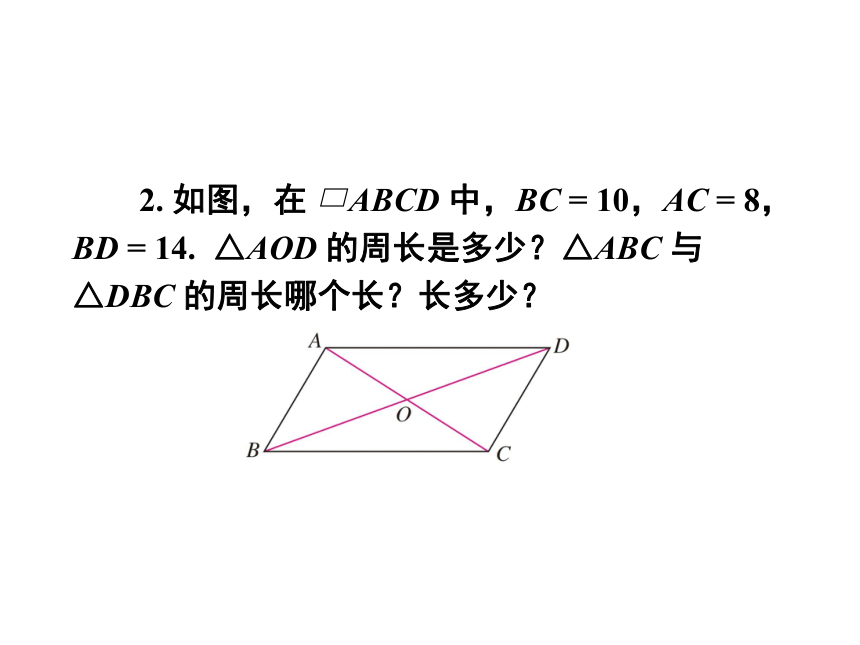
2. 如图,在 ABCD 中,BC = 10,AC = 8,BD = 14. △AOD 的周长是多少?△ABC 与△DBC 的周长哪个长?长多少?
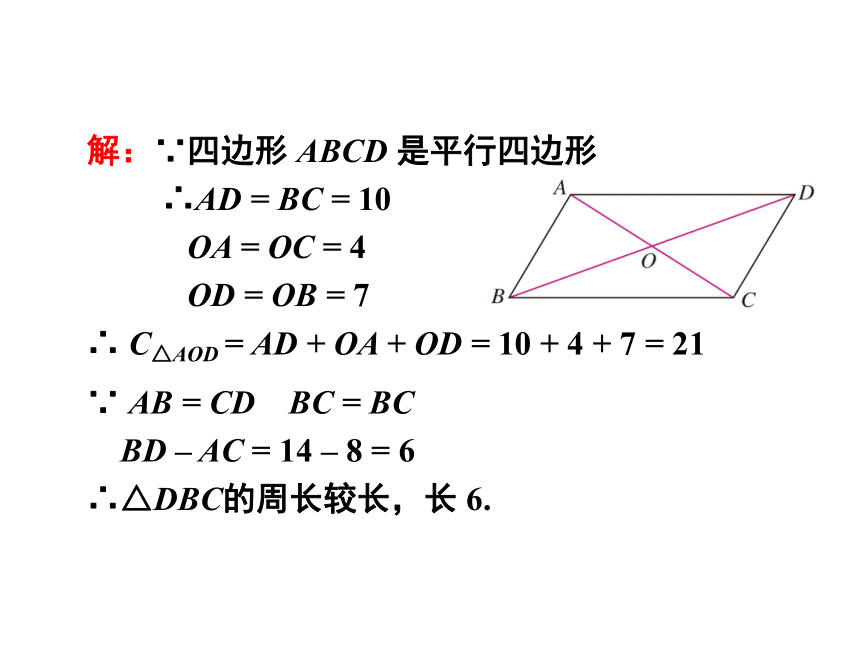
解:∵四边形 ABCD 是平行四边形
∴AD = BC = 10
OA = OC = 4
OD = OB = 7
∴ C△AOD = AD + OA + OD = 10 + 4 + 7 = 21
∵ AB = CD BC = BC
BD – AC = 14 – 8 = 6
∴△DBC的周长较长,长 6.
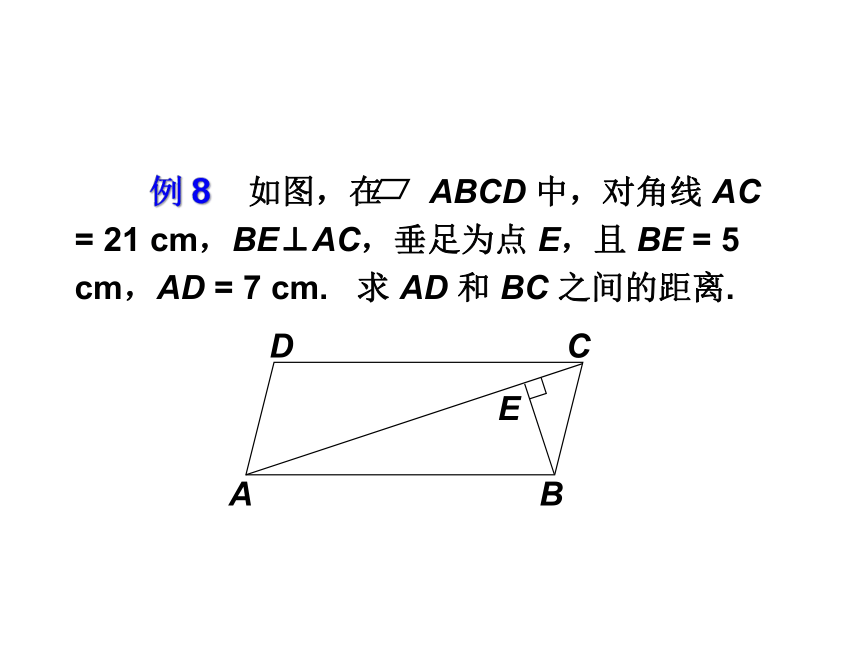
例 8 如图,在 ABCD 中,对角线 AC = 21 cm,BE⊥AC,垂足为点 E,且 BE = 5 cm,AD = 7 cm. 求 AD 和 BC 之间的距离.
A
B
C
D
E
A
B
C
D
E
解 设 AD 和 BC 之间的距离为 x,则
ABCD 的面积等于AD · x.
∵S ABCD = 2S△ABC = AC · BE,
∴AD · x = AC · BE,即 7x = 21×5,
∴ x = 15(cm).
即 AD 和 BC 之间
的距离为 15 cm.
练习
1. 如图,如果△AOB 与△AOD 的周长之差为 8,而 AB∶AD = 3∶2,那么 ABCD 的周长为多少?
D
A
B
C
O
D
A
B
C
O
解 ∵四边形 ABCD 是平行四边形,
∴OB = OD(平行四边形的对角线互相平分),
∵△AOD 的周长 + 8 = △AOB 的周长,
即 AD + 2 = AB.
又 AB∶AD = 3∶2 ,
∴AB = 24,BC = 16,
所以 ABCD 的周长是 2×(24+16)= 80.
2. 在 ABCD 中,两条对角线 AC 与 BD 相交于点 O,BC = 5,AC = 6,BD = 8. 求△AOB 的周长.
A
B
C
D
O
A
B
C
D
O
解 ∵四边形 ABCD 是平行四边形,
∴OB = OD = 4,OA = OC = 3,
又∵BC = 5,
OB2 + OC2 = 42 + 32 = 52 = BC2,
∴∠BOC = 90°,
∴AC⊥BD,
∴AB2 = OA2 + OA2 = 25,
∴AB = 5,
∴△AOB 的周长是 3 + 4 + 5 = 12.
课堂小结
谈谈你在这节课中,有什么收获?
随堂演练
1. ABCD 的周长为 40 cm,△ABC 的周长为 25 cm,则对角线 AC 长为( )
A. 5 cm B. 15 cm
C. 6 cm D. 16 cm
A
2. 平行四边形的两条对角线把它分成的四个三角形( )
A. 都是等腰三角形
B. 都是全等三角形
C. 都是直角三角形
D. 是面积相等的三角形
D
3. ABCD 中,AC、BD 相交于 O, ABCD的周长为 20 cm,△AOB 的周长比△BOC 的周长小 4 cm,则 AB =_____,BC =_____.
3cm
7cm
4. 一个平行四边形的一边长为 8,一条对角线长为 6,则另一条对角线 x 的取值范围为:_____________.
10<x<22
5.如图, ABCD 的对角线 AC,BD 相交于点 O,EF 过点 O 且与 AB,CD 分别相交于点 E,F. 求证:OE = OF.
证明:由平行四边形的性质 得:OB = OD. ∵AB∥CD,
∴∠EBO =∠FDO.
又∵∠EOB =∠FOD,
∴△EOB ≌ △FOD.
∴OE = OF.
6. 如图,在 ABCD 中,对角线 AC、BD相交于 O,AC = 6,BD = 8,AB = 5,
(1)求 ABCD 的周长;
(2)求 ABCD 的面积.
解:(1)由平行四边形的性质得:
OC = OA = AC = 3,OB = OD = BD = 4.
在△AOB 中,OA2 + OB2 = 32 + 42 = 52 = AB2.
∴△AOB 是直角三角形,∠AOB = 90°.
∴AC⊥BD.
(2)由(1)知:AC⊥BD
∴
新课导入
平行四边形有什么性质?
性质 1 平行四边形的对边相等
性质 2 平行四边形的对角相等
性质 3 平行四边形的对角线互相平分
新课探索
例 7? ?如图, ABCD 的对角线 AC 与 BD 相交于点 O,其周长为 16,且△ AOB 的周长比 △BOC 的周长小 2. 求边 AB 和 BC 的长.
A
B
C
D
O
A
B
C
D
O
解 ∵四边形 ABCD 是平行四边形,
∴OA = OC(平行四边形的对角线互相平分),
∵△AOB 的周长 + 2 = △BOC 的周长,
∴AB + OA + OB + 2 = BC + OB + OC,
即 AB + 2 = BC.
又∵ ABCD 的周长等于16,
∴2(AB + BC) = 16,
即 4AB + 4 = 16.
∴AB = 3,BC = 5.
练习
1. ABCD 的两条对角线 AC 与 BD 相交于点O,已知 AB = 8 cm,BC = 6 cm,△AOB
的周长是 18 cm. 求△AOD 的周长。
D
A
B
C
O
D
A
B
C
O
解 ∵ △AOB的周长是 18 cm ,AB = 8 cm ,
∴OA + OB = 10 cm,
又∵四边形 ABCD 是平行四边形,
∴OB = OD,AD = BC = 6 cm,
∴OA + OD = OA + OB = 10 cm,
∴△AOD 的周长
= AD + OA + OD
= 10 + 6 = 16 cm.
2. 如图,在 ABCD 中,BC = 10,AC = 8,BD = 14. △AOD 的周长是多少?△ABC 与△DBC 的周长哪个长?长多少?
解:∵四边形 ABCD 是平行四边形
∴AD = BC = 10
OA = OC = 4
OD = OB = 7
∴ C△AOD = AD + OA + OD = 10 + 4 + 7 = 21
∵ AB = CD BC = BC
BD – AC = 14 – 8 = 6
∴△DBC的周长较长,长 6.
例 8 如图,在 ABCD 中,对角线 AC = 21 cm,BE⊥AC,垂足为点 E,且 BE = 5 cm,AD = 7 cm. 求 AD 和 BC 之间的距离.
A
B
C
D
E
A
B
C
D
E
解 设 AD 和 BC 之间的距离为 x,则
ABCD 的面积等于AD · x.
∵S ABCD = 2S△ABC = AC · BE,
∴AD · x = AC · BE,即 7x = 21×5,
∴ x = 15(cm).
即 AD 和 BC 之间
的距离为 15 cm.
练习
1. 如图,如果△AOB 与△AOD 的周长之差为 8,而 AB∶AD = 3∶2,那么 ABCD 的周长为多少?
D
A
B
C
O
D
A
B
C
O
解 ∵四边形 ABCD 是平行四边形,
∴OB = OD(平行四边形的对角线互相平分),
∵△AOD 的周长 + 8 = △AOB 的周长,
即 AD + 2 = AB.
又 AB∶AD = 3∶2 ,
∴AB = 24,BC = 16,
所以 ABCD 的周长是 2×(24+16)= 80.
2. 在 ABCD 中,两条对角线 AC 与 BD 相交于点 O,BC = 5,AC = 6,BD = 8. 求△AOB 的周长.
A
B
C
D
O
A
B
C
D
O
解 ∵四边形 ABCD 是平行四边形,
∴OB = OD = 4,OA = OC = 3,
又∵BC = 5,
OB2 + OC2 = 42 + 32 = 52 = BC2,
∴∠BOC = 90°,
∴AC⊥BD,
∴AB2 = OA2 + OA2 = 25,
∴AB = 5,
∴△AOB 的周长是 3 + 4 + 5 = 12.
课堂小结
谈谈你在这节课中,有什么收获?
随堂演练
1. ABCD 的周长为 40 cm,△ABC 的周长为 25 cm,则对角线 AC 长为( )
A. 5 cm B. 15 cm
C. 6 cm D. 16 cm
A
2. 平行四边形的两条对角线把它分成的四个三角形( )
A. 都是等腰三角形
B. 都是全等三角形
C. 都是直角三角形
D. 是面积相等的三角形
D
3. ABCD 中,AC、BD 相交于 O, ABCD的周长为 20 cm,△AOB 的周长比△BOC 的周长小 4 cm,则 AB =_____,BC =_____.
3cm
7cm
4. 一个平行四边形的一边长为 8,一条对角线长为 6,则另一条对角线 x 的取值范围为:_____________.
10<x<22
5.如图, ABCD 的对角线 AC,BD 相交于点 O,EF 过点 O 且与 AB,CD 分别相交于点 E,F. 求证:OE = OF.
证明:由平行四边形的性质 得:OB = OD. ∵AB∥CD,
∴∠EBO =∠FDO.
又∵∠EOB =∠FOD,
∴△EOB ≌ △FOD.
∴OE = OF.
6. 如图,在 ABCD 中,对角线 AC、BD相交于 O,AC = 6,BD = 8,AB = 5,
(1)求 ABCD 的周长;
(2)求 ABCD 的面积.
解:(1)由平行四边形的性质得:
OC = OA = AC = 3,OB = OD = BD = 4.
在△AOB 中,OA2 + OB2 = 32 + 42 = 52 = AB2.
∴△AOB 是直角三角形,∠AOB = 90°.
∴AC⊥BD.
(2)由(1)知:AC⊥BD
∴
