华东师大版数学八年级下册课件:18.2.1 平行四边形的判定定理1、2(共26张PPT)
文档属性
| 名称 | 华东师大版数学八年级下册课件:18.2.1 平行四边形的判定定理1、2(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 658.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 13:32:51 | ||
图片预览





文档简介
第1课时 平行四边形的判定定理1、2
18.2 平行四边形的判定
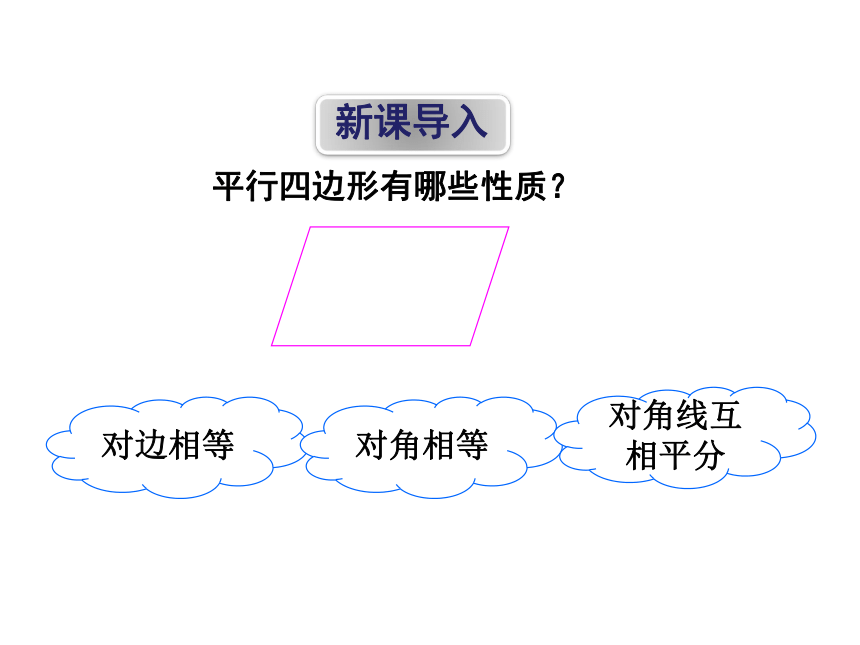
新课导入
平行四边形有哪些性质?
对边相等
对角相等
对角线互相平分
新课探索
那么,怎样判定一个四边形是否是平行四边形呢?
根据平行四边形的定义加以判定:两组对边分别平行的四边形是平行四边形。
除此之外,是否还存在其他的判定方法?
思考
由平行四边形的性质“平行四边形的两组对边分别相等”,逆向思考,互换条件与结论,试写出它的逆命题.
条件
结论
平行四边形的两组对边分别相等
逆命题
一个四边形是平行四边形
这个四边形的两组对边分别相等
一个四边形的两组对边分别相等
这个四边形是平行四边形
你认为它是真命题吗?
试
一
试
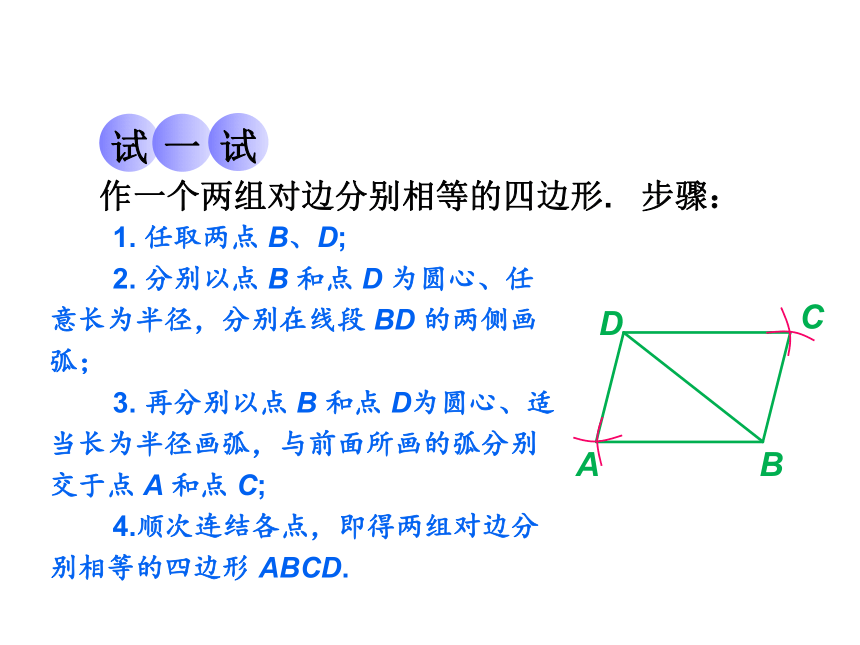
作一个两组对边分别相等的四边形. 步骤:
1. 任取两点 B、D;
2. 分别以点 B 和点 D 为圆心、任意长为半径,分别在线段 BD 的两侧画弧;
3. 再分别以点 B 和点 D为圆心、适当长为半径画弧,与前面所画的弧分别交于点 A 和点 C;
4.顺次连结各点,即得两组对边分别相等的四边形 ABCD.
B
D
A
C
把你作的四边形和其他同学作的进行比较,看看是否都是平行四边形.
可以发现,尽管每个人取的边长不一样,但只要对边分别相等,所作的就都是平行四边形.
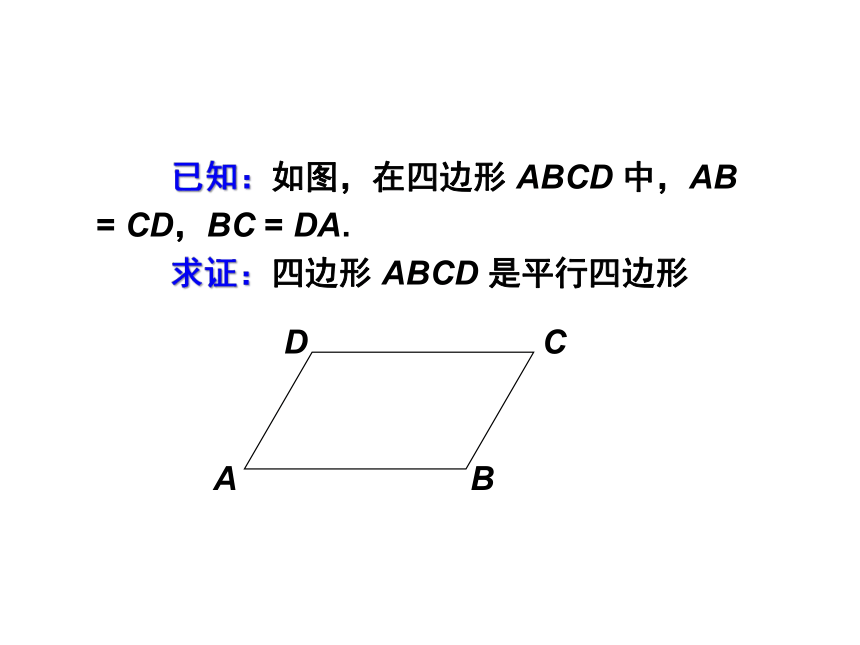
平行四边形的判定定理 1 两组对边分别相等的四边形是平行四边形.
已知:如图,在四边形 ABCD 中,AB = CD,BC = DA.
求证:四边形 ABCD 是平行四边形
A
B
C
D
A
B
C
D
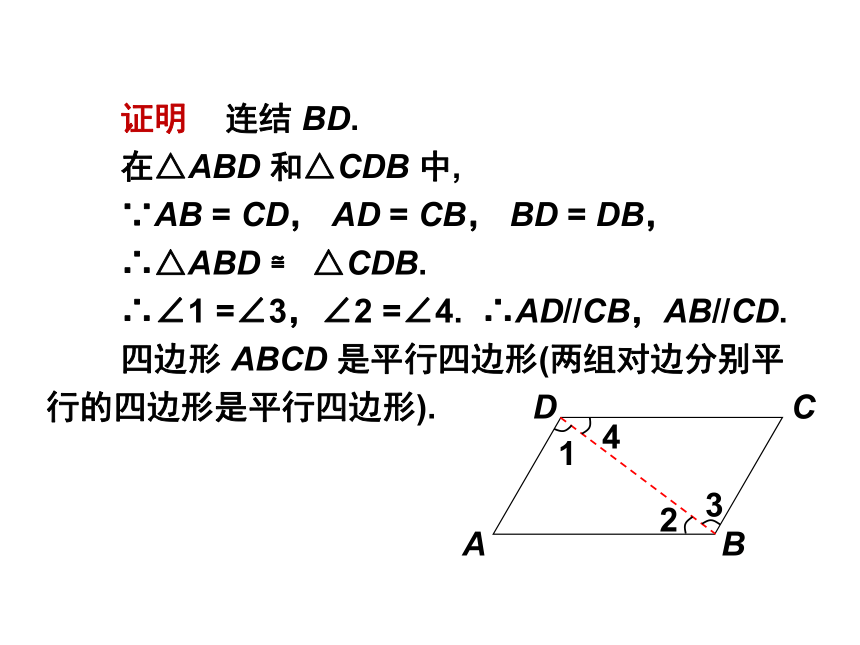
证明?? 连结 BD.
在△ABD 和△CDB 中,
∵AB =?CD,?AD =?CB,?BD =?DB,
∴△ABD ≌ △CDB.
∴∠1 =∠3,∠2 =∠4. ∴AD//CB,AB//CD.
四边形 ABCD 是平行四边形(两组对边分别平行的四边形是平行四边形).
1
2
3
4
如果只知道四边形的一组对边相等,从边的角度看,加一个什么条件能使下式成立:
一组对边相等
+
平行四边形
这组对边平行
你能证明吗?
试
一
试
作一个有一组对边平行且相等的四边形. 步骤:
1. 任意画两条平行线 m、n;
2. 在直线 m、n 上分别截取 AB、CD,使 AB = CD;
3. 分别连结点 B、C 和点 A、D,即得到一组对边平行且相等的四边形 ABCD.
n
m
A
B
C
D
四边形 ABCD 是平行四边形
已知:如图,在四边形 ABCD 中,AB∥CD 且 AB = CD.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
A
B
C
D
1
2
证明 连结对角线 AC.
在△ABC 和△CDA 中,
∵AB // CD,∴∠1 =∠2.
又∵AB = CD,AC = CA,
∴△ABC ≌△CDA. ∴BC = DA.
四边形 ABCD 是平行四边形(两组对边分别相等的四边形是平行四边形).
平行四边形的判定定理 2 一组对边平行且相等的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形.
AB ∥ CD,AD ∥ BC,
ABCD 是平行四边形.
总
结
A
B
C
D
两组对边分别相等的四边形是平行四边形.
AB = CD,AD = BC,
ABCD 是平行四边形.
A
B
C
D
一组对边平行且相等的四边形是平行四边形.
AB = CD,AB ∥ CD,
ABCD 是平行四边形.
A
B
C
D
例 1 如图,在 ABCD 中,点 E、F 分别在对边 BC 和 DA 上,且 AF = CE.
求证:四边形 AECF 是平行四边形.
B
C
D
A
E
F
证明 ∵四边形 ABCD 是平行四边形,
∴AD//CB(平行四边形的对边平行),
即AF//CE.
又∵AF = CE,
四边形 AECF 为平行四边形(一组对边平行且相等的四边形是平行四边形).
B
C
D
A
E
F
练习
已知:在四边形 ABCD 中,AB∥CD,要使四边形 ABCD 为平行四边形,需添加一个条件是什么?
A
B
C
D
AD∥BC 或 AB = CD
课堂小结
平行四边形的判定定理 1 两组对边分别相等的四边形是平行四边形.
平行四边形的判定定理 2 一组对边平行且相等的四边形是平行四边形.
随堂演练
1.如图,△ABC 平移后得到△DEF,则图中的平行四边形分别有____________________________.
ACFD、 ABED、 BCFE
2. 如图,AB = DC = EF,AD = BC,DE = CF.
求证:AB∥EF.
证明:∵ AB = DC,AD = BC,
∴ 四边形 ABCD 是平行四边形.
∴ AB∥DC.
又∵DC = EF,DE = CF,
∴ 四边形 DCFE 也是平行四边形.
∴ DC∥EF.∴ AB∥EF.
3. 如图,在 ABCD 中,BD 是它的一条对角线,过 A,C 两点分别作 AE⊥BD,CF⊥BD,E,F 为垂足.求证:四边形 AFCE 是平行四边形.
证明:∵四边形 ABCD 为平行四边形,
∴AD = BC,AD∥BC,∴∠ADE =∠CBF,
又∵∠AED =∠CFB = 90°,∴△AED ≌△CFB,
∴AE = CF.
又∵∠AEF =∠CFE = 90°,
∴ AE∥CF,
∴四边形 AFCE 是平行四边形.
4. 如图,DB∥AC,DB = AC,E 是 AC的中点,求证:BC = DE.
证明:∵E 为 AC 的中点,DB = AC,
∴DB = CE. 又∵DB∥AC,
即 DB∥CE,
∴四边形 BCED 为平行四边形,
∴BC = DE.
18.2 平行四边形的判定
新课导入
平行四边形有哪些性质?
对边相等
对角相等
对角线互相平分
新课探索
那么,怎样判定一个四边形是否是平行四边形呢?
根据平行四边形的定义加以判定:两组对边分别平行的四边形是平行四边形。
除此之外,是否还存在其他的判定方法?
思考
由平行四边形的性质“平行四边形的两组对边分别相等”,逆向思考,互换条件与结论,试写出它的逆命题.
条件
结论
平行四边形的两组对边分别相等
逆命题
一个四边形是平行四边形
这个四边形的两组对边分别相等
一个四边形的两组对边分别相等
这个四边形是平行四边形
你认为它是真命题吗?
试
一
试
作一个两组对边分别相等的四边形. 步骤:
1. 任取两点 B、D;
2. 分别以点 B 和点 D 为圆心、任意长为半径,分别在线段 BD 的两侧画弧;
3. 再分别以点 B 和点 D为圆心、适当长为半径画弧,与前面所画的弧分别交于点 A 和点 C;
4.顺次连结各点,即得两组对边分别相等的四边形 ABCD.
B
D
A
C
把你作的四边形和其他同学作的进行比较,看看是否都是平行四边形.
可以发现,尽管每个人取的边长不一样,但只要对边分别相等,所作的就都是平行四边形.
平行四边形的判定定理 1 两组对边分别相等的四边形是平行四边形.
已知:如图,在四边形 ABCD 中,AB = CD,BC = DA.
求证:四边形 ABCD 是平行四边形
A
B
C
D
A
B
C
D
证明?? 连结 BD.
在△ABD 和△CDB 中,
∵AB =?CD,?AD =?CB,?BD =?DB,
∴△ABD ≌ △CDB.
∴∠1 =∠3,∠2 =∠4. ∴AD//CB,AB//CD.
四边形 ABCD 是平行四边形(两组对边分别平行的四边形是平行四边形).
1
2
3
4
如果只知道四边形的一组对边相等,从边的角度看,加一个什么条件能使下式成立:
一组对边相等
+
平行四边形
这组对边平行
你能证明吗?
试
一
试
作一个有一组对边平行且相等的四边形. 步骤:
1. 任意画两条平行线 m、n;
2. 在直线 m、n 上分别截取 AB、CD,使 AB = CD;
3. 分别连结点 B、C 和点 A、D,即得到一组对边平行且相等的四边形 ABCD.
n
m
A
B
C
D
四边形 ABCD 是平行四边形
已知:如图,在四边形 ABCD 中,AB∥CD 且 AB = CD.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
A
B
C
D
1
2
证明 连结对角线 AC.
在△ABC 和△CDA 中,
∵AB // CD,∴∠1 =∠2.
又∵AB = CD,AC = CA,
∴△ABC ≌△CDA. ∴BC = DA.
四边形 ABCD 是平行四边形(两组对边分别相等的四边形是平行四边形).
平行四边形的判定定理 2 一组对边平行且相等的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形.
AB ∥ CD,AD ∥ BC,
ABCD 是平行四边形.
总
结
A
B
C
D
两组对边分别相等的四边形是平行四边形.
AB = CD,AD = BC,
ABCD 是平行四边形.
A
B
C
D
一组对边平行且相等的四边形是平行四边形.
AB = CD,AB ∥ CD,
ABCD 是平行四边形.
A
B
C
D
例 1 如图,在 ABCD 中,点 E、F 分别在对边 BC 和 DA 上,且 AF = CE.
求证:四边形 AECF 是平行四边形.
B
C
D
A
E
F
证明 ∵四边形 ABCD 是平行四边形,
∴AD//CB(平行四边形的对边平行),
即AF//CE.
又∵AF = CE,
四边形 AECF 为平行四边形(一组对边平行且相等的四边形是平行四边形).
B
C
D
A
E
F
练习
已知:在四边形 ABCD 中,AB∥CD,要使四边形 ABCD 为平行四边形,需添加一个条件是什么?
A
B
C
D
AD∥BC 或 AB = CD
课堂小结
平行四边形的判定定理 1 两组对边分别相等的四边形是平行四边形.
平行四边形的判定定理 2 一组对边平行且相等的四边形是平行四边形.
随堂演练
1.如图,△ABC 平移后得到△DEF,则图中的平行四边形分别有____________________________.
ACFD、 ABED、 BCFE
2. 如图,AB = DC = EF,AD = BC,DE = CF.
求证:AB∥EF.
证明:∵ AB = DC,AD = BC,
∴ 四边形 ABCD 是平行四边形.
∴ AB∥DC.
又∵DC = EF,DE = CF,
∴ 四边形 DCFE 也是平行四边形.
∴ DC∥EF.∴ AB∥EF.
3. 如图,在 ABCD 中,BD 是它的一条对角线,过 A,C 两点分别作 AE⊥BD,CF⊥BD,E,F 为垂足.求证:四边形 AFCE 是平行四边形.
证明:∵四边形 ABCD 为平行四边形,
∴AD = BC,AD∥BC,∴∠ADE =∠CBF,
又∵∠AED =∠CFB = 90°,∴△AED ≌△CFB,
∴AE = CF.
又∵∠AEF =∠CFE = 90°,
∴ AE∥CF,
∴四边形 AFCE 是平行四边形.
4. 如图,DB∥AC,DB = AC,E 是 AC的中点,求证:BC = DE.
证明:∵E 为 AC 的中点,DB = AC,
∴DB = CE. 又∵DB∥AC,
即 DB∥CE,
∴四边形 BCED 为平行四边形,
∴BC = DE.
