华东师大版数学八年级下册课件:18.2.2平行四边形的判定定理3(共24张PPT)
文档属性
| 名称 | 华东师大版数学八年级下册课件:18.2.2平行四边形的判定定理3(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 473.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 13:34:15 | ||
图片预览





文档简介
第2课时
平行四边形的判定定理3
新课导入
我们已经学行四边形的哪些判定定理?
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
除此之外,是否还存在其他的判定方法?
新课探索
思考
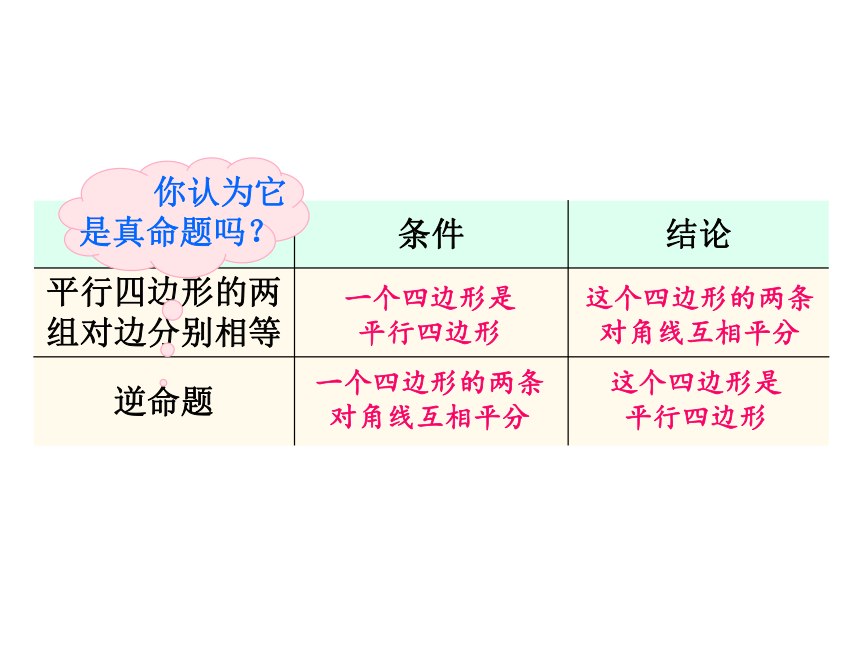
由平行四边形的性质“平行四边形的两条对角线互相平分”,逆向思考,互换条件与结论,试写出它的逆命题.
条件
结论
平行四边形的两组对边分别相等
逆命题
一个四边形是平行四边形
这个四边形的两条对角线互相平分
一个四边形的两条对角线互相平分
这个四边形是平行四边形
你认为它是真命题吗?
试
一
试
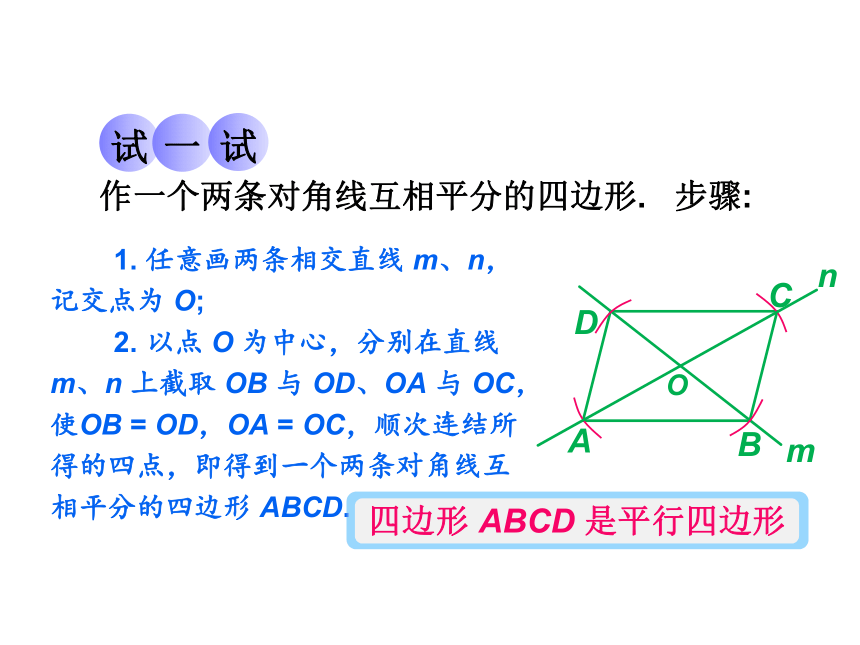
作一个两条对角线互相平分的四边形.
步骤:
1.
任意画两条相交直线
m、n,记交点为
O;
2.
以点
O
为中心,分别在直线
m、n
上截取
OB
与
OD、OA
与
OC,使OB
=
OD,OA
=
OC,顺次连结所得的四点,即得到一个两条对角线互相平分的四边形
ABCD.
B
D
A
C
O
n
m
四边形
ABCD
是平行四边形
平行四边形的判定定理
3
对角线互相平分的四边形是平行四边形.
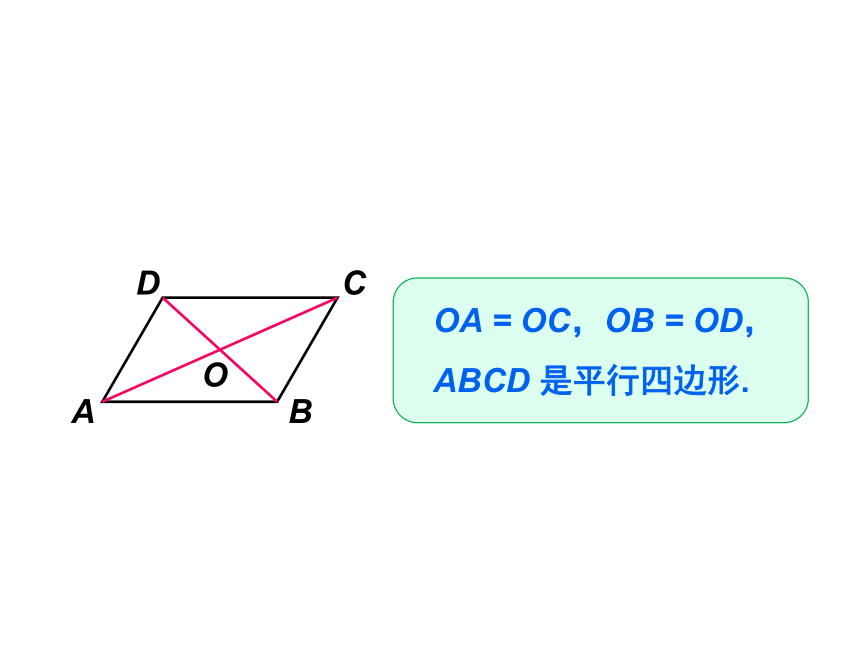
OA
=
OC,OB
=
OD,
ABCD
是平行四边形.
A
B
C
D
O
已知:如图,在四边形
ABCD
中,对角线
AC
和
BD
相交于点
O,OA
=
OC,OB
=
OD.
求证:四边形
ABCD
是平行四边形
A
B
C
D
O
A
B
C
D
O
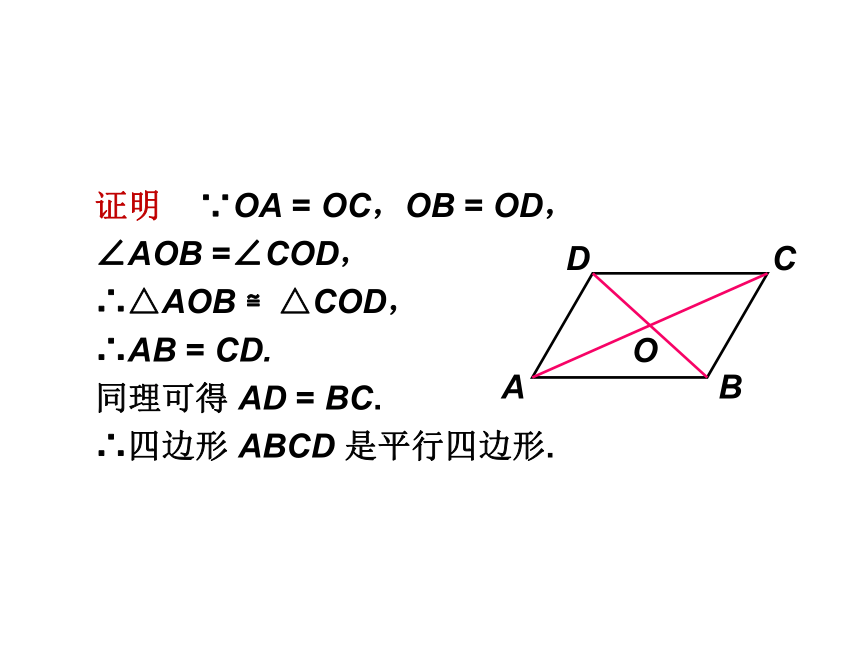
证明
∵OA
=
OC,OB
=
OD,
∠AOB
=∠COD,
∴△AOB
≌△COD,
∴AB
=
CD.
同理可得
AD
=
BC.
∴四边形
ABCD
是平行四边形.
例
2
如图,在
ABCD
中,点
E、F
是对角线
AC
上的两点,且
AE
=
CF.
求证:四边形
BFDE
是平行四边形.
A
B
C
D
O
E
F
证明
连结
BD,交
AC
于点
O.
∵四边形
ABCD
是平行四边形,
∴OB
=
OD,
OA
=
OC
(平行四边形的对角线互相平分).
又∵
AE
=
CF
,
∴OA
–
AE
=
OC
–
CF.
即
OE
=
OF,
∴四边形
BFDE
是平行四边形(对角线互相平分的四边形是平行四边形).
A
B
C
D
O
E
F
如图,在□
ABCD
中,对角线
AC
与
BD
相交于点
O,点
E,F
分别是
OA
和
OC
的中点,四边形
BFDE
是平行四边形吗?请说明理由.
练习
证明
四边形
BFDE
是平行四边形.
∵四边形
ABCD
是平行四边形,
∴OB
=
OD,
OA
=
OC
(平行四边形的对角线互相平分).
又∵
OE
=
OA
,
OF
=
OC.
∴
OE
=
OF,
∴四边形
BFDE
是平行四边形(对角线互相平分的四边形是平行四边形).
1
2
1
2
我们知道平行四边形的对角相等,那么反过来,对角相等的四边形是平行四边形吗?请你试着证明.
思考
已知:如图,在四边形
ABCD
中∠A
=∠C,∠B
=∠D.
求证:四边形
ABCD是平行四边形.
证明:∵∠A
=∠C,∠B
=∠D,
∠A
+∠C
+∠B
+∠D
=
360°,
∴∠A
+∠B
=
180°.
∴AD∥CB,
同理可得:AB∥CD.
∴四边形
ABCD
是平行四边形(平行四边形的定义).
读
一
读
由平行四边形的性质,联想平行四边形的判定方法,通过合情推理,提出猜想.
这是一个由原命题到逆命题的逆向思维的过程,今后在探索和研究其他几何问题时还会继续运用.
课堂小结
总
结
1.
两组对边分别平行的四边形是平行四边形
2.
两组对边分别相等的四边形是平行四边形
3.
一组对边平行且相等的四边形是平行四边形
4.
两组对角分别相等的四边形是平行四边形
5.两条对角线互相平分的四边形是平行四边形
随堂演练
1.
判断下列说法是否正确
(1)一组对边平行且另一组对边相等的四边形是平行四边形.
(
)
(2)两组对角都相等的四边形是平行四边形.
(
)
×
√
(3)一组对边平行且一组对角相等的四边形是平行四边形.
(
)
(4)一组对边平行,一组邻角互补的四边形是平行四边形.
(
)
×
√
2.
如图所示,D
为△ABC
的边
AB
上一点,DF
交
AC
于点
E,且
AE
=
CE,FC∥AB.
求证:CD
=
AF.
证明:∵FC∥AB,
∴∠DAC
=∠ACF,∠ADF
=∠DFC.
又∵AE
=
CE,
∴△ADE
≌△CFE(AAS),
∴DE
=
EF.
∵AE
=
CE,
∴四边形
ADCF
为平行四边形.
∴CD
=
AF.
3.
如图,□
ABCD
中,对角线
AC,BD
相交于点
O,过点
O
作两条直线分别与
AB,BC,CD,AD
交于
G,F,H,E
四点.
求证:四边形
EGFH
是平行四边形
.
证明:∵四边形
ABCD
是平行四边形,
∴AO
=
CO,AD∥CB.
∴∠OAE
=∠OCF.
又∵∠AOE
=∠COF,
△AOE
≌△COF(ASA),
∴OE
=
OF,
同理可得:OG
=
OH.
∴四边形
EGFH
为平行四边形.
平行四边形的判定定理3
新课导入
我们已经学行四边形的哪些判定定理?
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
除此之外,是否还存在其他的判定方法?
新课探索
思考
由平行四边形的性质“平行四边形的两条对角线互相平分”,逆向思考,互换条件与结论,试写出它的逆命题.
条件
结论
平行四边形的两组对边分别相等
逆命题
一个四边形是平行四边形
这个四边形的两条对角线互相平分
一个四边形的两条对角线互相平分
这个四边形是平行四边形
你认为它是真命题吗?
试
一
试
作一个两条对角线互相平分的四边形.
步骤:
1.
任意画两条相交直线
m、n,记交点为
O;
2.
以点
O
为中心,分别在直线
m、n
上截取
OB
与
OD、OA
与
OC,使OB
=
OD,OA
=
OC,顺次连结所得的四点,即得到一个两条对角线互相平分的四边形
ABCD.
B
D
A
C
O
n
m
四边形
ABCD
是平行四边形
平行四边形的判定定理
3
对角线互相平分的四边形是平行四边形.
OA
=
OC,OB
=
OD,
ABCD
是平行四边形.
A
B
C
D
O
已知:如图,在四边形
ABCD
中,对角线
AC
和
BD
相交于点
O,OA
=
OC,OB
=
OD.
求证:四边形
ABCD
是平行四边形
A
B
C
D
O
A
B
C
D
O
证明
∵OA
=
OC,OB
=
OD,
∠AOB
=∠COD,
∴△AOB
≌△COD,
∴AB
=
CD.
同理可得
AD
=
BC.
∴四边形
ABCD
是平行四边形.
例
2
如图,在
ABCD
中,点
E、F
是对角线
AC
上的两点,且
AE
=
CF.
求证:四边形
BFDE
是平行四边形.
A
B
C
D
O
E
F
证明
连结
BD,交
AC
于点
O.
∵四边形
ABCD
是平行四边形,
∴OB
=
OD,
OA
=
OC
(平行四边形的对角线互相平分).
又∵
AE
=
CF
,
∴OA
–
AE
=
OC
–
CF.
即
OE
=
OF,
∴四边形
BFDE
是平行四边形(对角线互相平分的四边形是平行四边形).
A
B
C
D
O
E
F
如图,在□
ABCD
中,对角线
AC
与
BD
相交于点
O,点
E,F
分别是
OA
和
OC
的中点,四边形
BFDE
是平行四边形吗?请说明理由.
练习
证明
四边形
BFDE
是平行四边形.
∵四边形
ABCD
是平行四边形,
∴OB
=
OD,
OA
=
OC
(平行四边形的对角线互相平分).
又∵
OE
=
OA
,
OF
=
OC.
∴
OE
=
OF,
∴四边形
BFDE
是平行四边形(对角线互相平分的四边形是平行四边形).
1
2
1
2
我们知道平行四边形的对角相等,那么反过来,对角相等的四边形是平行四边形吗?请你试着证明.
思考
已知:如图,在四边形
ABCD
中∠A
=∠C,∠B
=∠D.
求证:四边形
ABCD是平行四边形.
证明:∵∠A
=∠C,∠B
=∠D,
∠A
+∠C
+∠B
+∠D
=
360°,
∴∠A
+∠B
=
180°.
∴AD∥CB,
同理可得:AB∥CD.
∴四边形
ABCD
是平行四边形(平行四边形的定义).
读
一
读
由平行四边形的性质,联想平行四边形的判定方法,通过合情推理,提出猜想.
这是一个由原命题到逆命题的逆向思维的过程,今后在探索和研究其他几何问题时还会继续运用.
课堂小结
总
结
1.
两组对边分别平行的四边形是平行四边形
2.
两组对边分别相等的四边形是平行四边形
3.
一组对边平行且相等的四边形是平行四边形
4.
两组对角分别相等的四边形是平行四边形
5.两条对角线互相平分的四边形是平行四边形
随堂演练
1.
判断下列说法是否正确
(1)一组对边平行且另一组对边相等的四边形是平行四边形.
(
)
(2)两组对角都相等的四边形是平行四边形.
(
)
×
√
(3)一组对边平行且一组对角相等的四边形是平行四边形.
(
)
(4)一组对边平行,一组邻角互补的四边形是平行四边形.
(
)
×
√
2.
如图所示,D
为△ABC
的边
AB
上一点,DF
交
AC
于点
E,且
AE
=
CE,FC∥AB.
求证:CD
=
AF.
证明:∵FC∥AB,
∴∠DAC
=∠ACF,∠ADF
=∠DFC.
又∵AE
=
CE,
∴△ADE
≌△CFE(AAS),
∴DE
=
EF.
∵AE
=
CE,
∴四边形
ADCF
为平行四边形.
∴CD
=
AF.
3.
如图,□
ABCD
中,对角线
AC,BD
相交于点
O,过点
O
作两条直线分别与
AB,BC,CD,AD
交于
G,F,H,E
四点.
求证:四边形
EGFH
是平行四边形
.
证明:∵四边形
ABCD
是平行四边形,
∴AO
=
CO,AD∥CB.
∴∠OAE
=∠OCF.
又∵∠AOE
=∠COF,
△AOE
≌△COF(ASA),
∴OE
=
OF,
同理可得:OG
=
OH.
∴四边形
EGFH
为平行四边形.
