华师大版七年级数学下册第九章第二节《多边形的内角和与外角和》第2课时教学课件 (共16张PPT)
文档属性
| 名称 | 华师大版七年级数学下册第九章第二节《多边形的内角和与外角和》第2课时教学课件 (共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 23.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 00:00:00 | ||
图片预览



文档简介
多边形的内角和
与外角和(2)
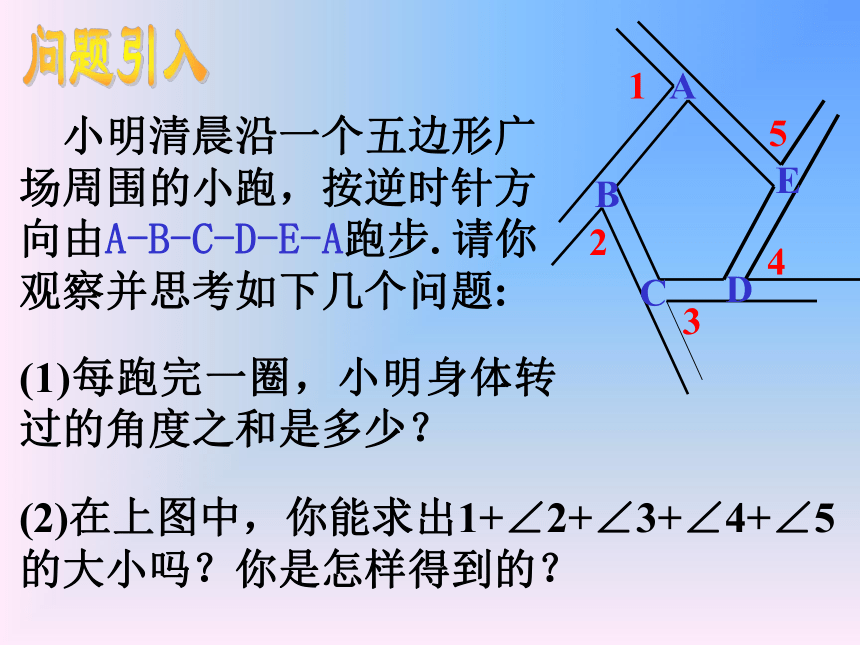
小明清晨沿一个五边形广场周围的小跑,按逆时针方向由A-B-C-D-E-A跑步. 请你观察并思考如下几个问题:
A
B
C
D
E
1
2
3
4
5
(1)每跑完一圈,小明身体转过的角度之和是多少?
(2)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?
问题引入
巩固复习:
1、十二边形内角和为( )
1800°
2、多边形内角和为1620°则它是
( )边形。
十一
n边形的内角和为:
(n -2)×180°
自主学习
阅读教材 最后自然段,思考并完成问题1:什么叫多边形的外角和?
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和
三角形的外角和就是三个外角的和
______
______
______
∠4
∠5
∠6
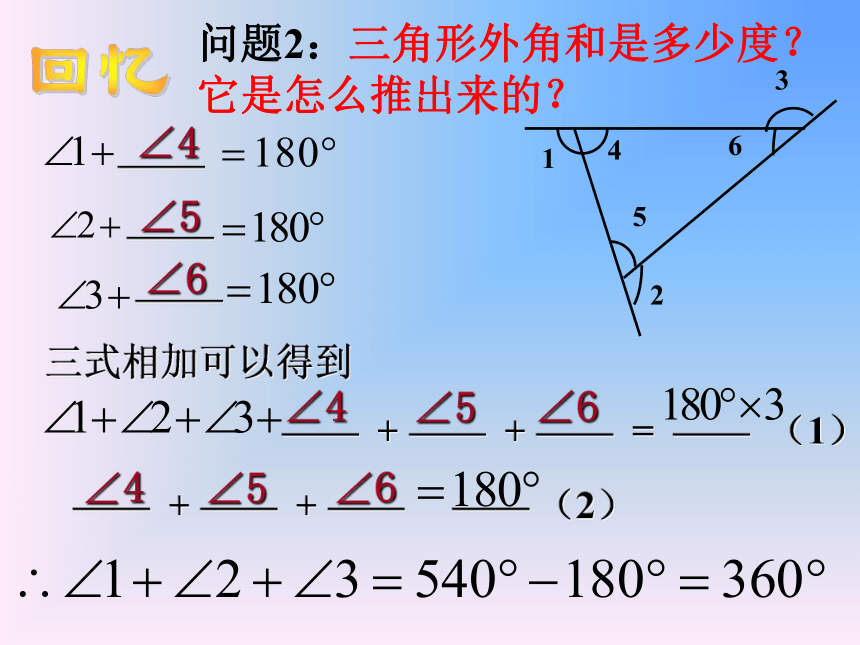
三式相加可以得到
—— + —— + —— = —— (1)
1
2
3
4
5
6
回忆
问题2:三角形外角和是多少度?
它是怎么推出来的?
∠4
∠5
∠6
—— + —— + —— —— (2)
∠4
∠5
∠6
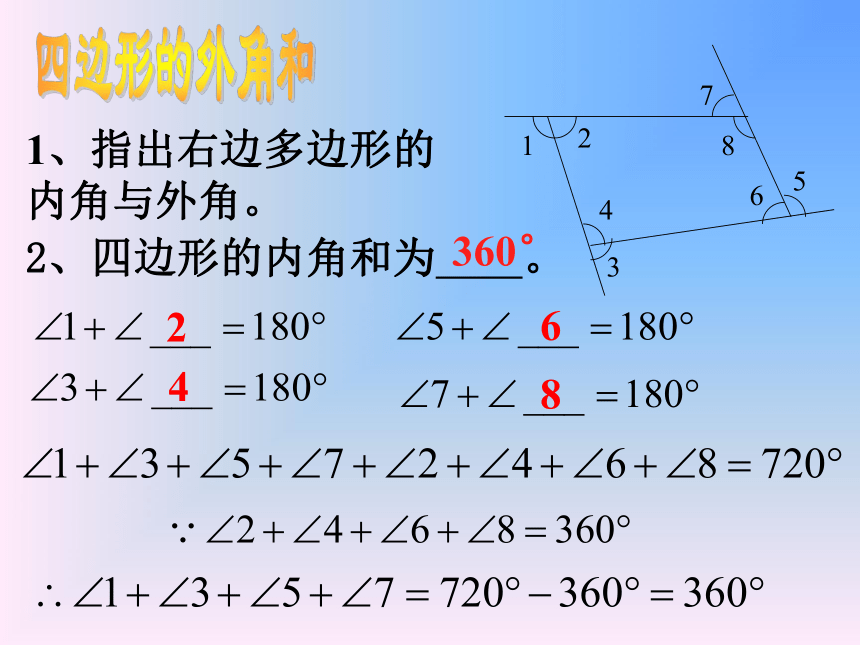
1、指出右边多边形的内角与外角。
1
3
5
7
2
4
6
8
2、四边形的内角和为 。
360°
四边形的外角和
2
4
6
8
3
2
1
4
3
2
1
5
4
3
2
1
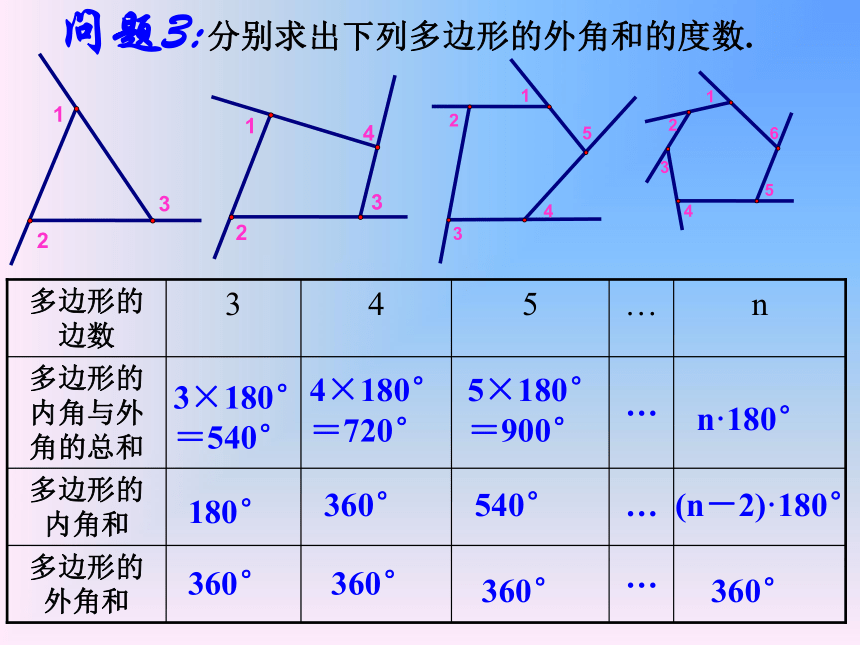
问题3:分别求出下列多边形的外角和的度数.
6
5
4
3
2
1
多边形的外角和
多边形的内角和
多边形的内角与外角的总和
n
…
5
4
3
多边形的边数
3×180°=540°
(n-2)·180°
…
n·180°
…
…
4×180°=720°
5×180°=900°
180°
360°
540°
360°
360°
360°
360°
问题4:
一个多边形的每个外角都是36°,这个多边形是几边形?
你想到了几种方法?
方法1:设这个多边形的边数为
则有:
解得:
方法2:
设这个多边形的边数为
则有:
解得:
哪种方法更简单呢?
n边形的外角和为360°
例:一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是
(n-2) ×180°,
(n-2) ×180° = 3×360°
解得:n=8
答:这个多边形是八边形.
外角和等于360°,
新知运用
1、一个十边形的每一个内角都相等,
那么这个十边形的每一外角等于( )
A、144° B、 72 ° C、 36° D 、18°
2、一个多边形每一个外角都等于45°,
则这个多边形的内角和等于( )
A、 720° B、 675° C、 1080°D、945°
C
C
巩固练习:
学习反馈:
1.一个多边形的每个外角都等于45°,这个多边形是 边形,它的每一个内角是 度.
2.一个多边形的内角和等于它外角和的4倍,这个多边形是 边形.
八
135°
十
你做对了吗?
达标检测:
1、一个多边形的边数增加时,其外角和 ( )
A、增加 B、减少 C、不变 D、不能确定
2、正多边形的一个外角是30°,则这是 边形。
3、若一个十边形的每个外角都相等,则它的每个外角的度数为_______,每个内角的度数为_______.
4、一个多边形的内角和是外角和的3倍,则这个多边形边数为 。
C
十二
36°
144°
8
5、在各个内角都相等的多边形中,一个外角等于一个内角的 ,则这个多边形的边数为_____;
6、在一个多边形中,它的内角最多可以有 个是锐角.
7、如图所示,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,……,这样一直走下去,他第一次回到出发点A时,一共走了 m。
8
3
240
小 结
1、什么是多边形的外角和?
2、n边形的内角和与外角和是多少?
n边形的内角和为: (n -2)×180°
多边形的外角和为:360°
在每个顶点处取这个多边形的一个外角,
它们的和叫做这个多边形的外角和.
学习反思
1、通过本节课的学习,谈一谈你有哪些收获?
2、说一说你还有哪些疑问?
再见!
与外角和(2)
小明清晨沿一个五边形广场周围的小跑,按逆时针方向由A-B-C-D-E-A跑步. 请你观察并思考如下几个问题:
A
B
C
D
E
1
2
3
4
5
(1)每跑完一圈,小明身体转过的角度之和是多少?
(2)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?
问题引入
巩固复习:
1、十二边形内角和为( )
1800°
2、多边形内角和为1620°则它是
( )边形。
十一
n边形的内角和为:
(n -2)×180°
自主学习
阅读教材 最后自然段,思考并完成问题1:什么叫多边形的外角和?
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和
三角形的外角和就是三个外角的和
______
______
______
∠4
∠5
∠6
三式相加可以得到
—— + —— + —— = —— (1)
1
2
3
4
5
6
回忆
问题2:三角形外角和是多少度?
它是怎么推出来的?
∠4
∠5
∠6
—— + —— + —— —— (2)
∠4
∠5
∠6
1、指出右边多边形的内角与外角。
1
3
5
7
2
4
6
8
2、四边形的内角和为 。
360°
四边形的外角和
2
4
6
8
3
2
1
4
3
2
1
5
4
3
2
1
问题3:分别求出下列多边形的外角和的度数.
6
5
4
3
2
1
多边形的外角和
多边形的内角和
多边形的内角与外角的总和
n
…
5
4
3
多边形的边数
3×180°=540°
(n-2)·180°
…
n·180°
…
…
4×180°=720°
5×180°=900°
180°
360°
540°
360°
360°
360°
360°
问题4:
一个多边形的每个外角都是36°,这个多边形是几边形?
你想到了几种方法?
方法1:设这个多边形的边数为
则有:
解得:
方法2:
设这个多边形的边数为
则有:
解得:
哪种方法更简单呢?
n边形的外角和为360°
例:一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是
(n-2) ×180°,
(n-2) ×180° = 3×360°
解得:n=8
答:这个多边形是八边形.
外角和等于360°,
新知运用
1、一个十边形的每一个内角都相等,
那么这个十边形的每一外角等于( )
A、144° B、 72 ° C、 36° D 、18°
2、一个多边形每一个外角都等于45°,
则这个多边形的内角和等于( )
A、 720° B、 675° C、 1080°D、945°
C
C
巩固练习:
学习反馈:
1.一个多边形的每个外角都等于45°,这个多边形是 边形,它的每一个内角是 度.
2.一个多边形的内角和等于它外角和的4倍,这个多边形是 边形.
八
135°
十
你做对了吗?
达标检测:
1、一个多边形的边数增加时,其外角和 ( )
A、增加 B、减少 C、不变 D、不能确定
2、正多边形的一个外角是30°,则这是 边形。
3、若一个十边形的每个外角都相等,则它的每个外角的度数为_______,每个内角的度数为_______.
4、一个多边形的内角和是外角和的3倍,则这个多边形边数为 。
C
十二
36°
144°
8
5、在各个内角都相等的多边形中,一个外角等于一个内角的 ,则这个多边形的边数为_____;
6、在一个多边形中,它的内角最多可以有 个是锐角.
7、如图所示,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,……,这样一直走下去,他第一次回到出发点A时,一共走了 m。
8
3
240
小 结
1、什么是多边形的外角和?
2、n边形的内角和与外角和是多少?
n边形的内角和为: (n -2)×180°
多边形的外角和为:360°
在每个顶点处取这个多边形的一个外角,
它们的和叫做这个多边形的外角和.
学习反思
1、通过本节课的学习,谈一谈你有哪些收获?
2、说一说你还有哪些疑问?
再见!
