1.3线段的垂直平分线(1)-北师大版八年级数学下册课件(共26张PPT)
文档属性
| 名称 | 1.3线段的垂直平分线(1)-北师大版八年级数学下册课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 10:48:14 | ||
图片预览








文档简介
线段的垂直平分线(一)
北师大版数学八年级下册第一章第三节
学习目标
1.证明线段垂直平分线的性质定理及其逆命题。
2.灵活运用线段垂直平分线的有关知识进行证明或计算.
学习目标
探究新知
线段的垂直平分线
定义:经过线段的中点,并且垂直于这条线段的直线是线段的垂直平分线。
A
C
B
l
性质
判定
几何图形
线段的垂直平分线
1.垂直、平分
探究新知 1
线段的垂直平分线的性质
2.线段垂直平分线上的点到这条线段两端的距离相等
问题1:线段的垂直平分线有哪些性质?
(定义)
问题2:你能证明这个结论吗?
A
C
B
l
探究新知 1
线段的垂直平分线的性质
证明命题:线段垂直平分线上的点到这条线段两端的距离相等
已知:如图,直线l ⊥ AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
P
A
B
l
C
证明:∵l ⊥ AB
∴ ∠ PCA= ∠ PCB=90°
在 ΔPAC和Δ PBC中
AC=BC
∠ PCA= ∠ PCB
PC=PC
∴ ΔPAC ≌Δ PBC
∴PA=PB
探究新知 1
线段的垂直平分线的性质
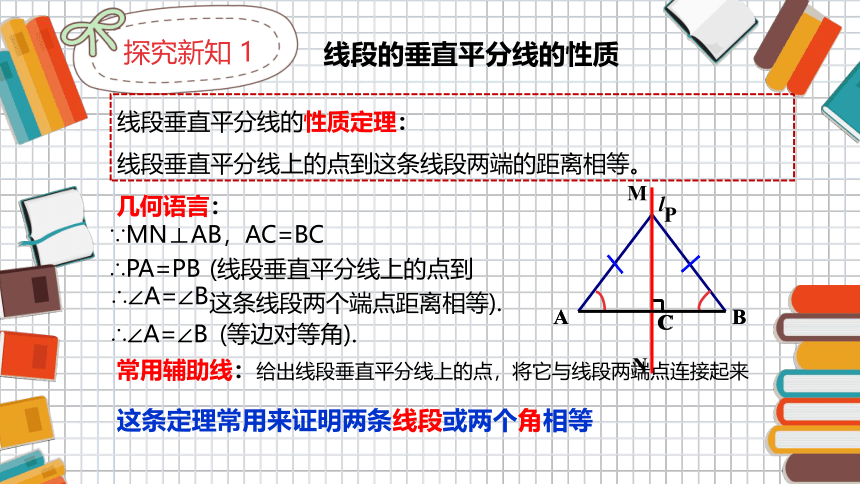
线段垂直平分线的性质定理:
线段垂直平分线上的点到这条线段两端的距离相等。
∵MN⊥AB,AC=BC
∴PA=PB
几何语言:
A
C
B
P
M
N
∴∠A=∠B
这条定理常用来证明两条线段或两个角相等
(线段垂直平分线上的点到
这条线段两个端点距离相等).
(等边对等角).
常用辅助线:给出线段垂直平分线上的点,将它与线段两端点连接起来
∴∠A=∠B
A
C
B
l
探究新知 1
线段的垂直平分线的性质
【例1】在△ABC 中,AB、AC 的垂直平分线相交于点O,分别交BC边于点M、N,连接AM,AN.
(1)若△AMN的周长为6,求BC的长;
(2)若∠MON=50°,求∠MAN的度数。
解:(1)∵M在AB的垂直平分线上
∴MA=MB
同理,NA=NC
∵△AMN的周长为6
∴MA+MN+NA=6
∴ BC= MB+MN+NC=6
(2)∵ MA=MB
∴∠1=∠B
同理, ∠2=∠C
∵∠MON=50°,OM ⊥AB, ON ⊥AC
∴∠BAC=360 °-90 °-90 °-50 °=130°
即∠1+ ∠MAN + ∠2=130°
1
2
又∵ ∠B+ ∠BAC + ∠C=180°
∴∠B+ ∠1+ ∠MAN + ∠2 + ∠C=180°
即2∠1+ ∠MAN + 2∠2=180°
∴∠1+ ∠2 =50°
∴∠MAN=130°﹣50°=80°
①
②
1.经过线段的中点,并且垂直于这条线段的直线是线段的垂直平分线。
探究新知 2
线段的垂直平分线的判定
2.
问题3:线段的垂直平分线有哪些判定方法?
(定义判定)
问题4:你能写出垂直平分线性质定理的逆命题吗?
?
性质定理的逆命题
?
探究新知 2
线段的垂直平分线的判定
性质定理(原命题):
如果一个点是线段垂直平分线上的点,那么这个点到这条线段两个端点的距离相等。
逆命题:
如果一个点到线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上。
问题5:这个逆命题是真命题吗?你能证明它吗?
探究新知 2
线段的垂直平分线的判定
证明逆命题:如果一个点到线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上。
已知:如图,线段AB,
求证:
A
B
P
PA=PB
点P在AB的垂直平分线上.
∵PA=PB
∴△PAB是等腰三角形
过点P作PC⊥AB,垂足为点C
∴ AC=BC
即PC垂直平分AB
∴点P在AB的垂直平分线上
证明
(1):
分析:
由PA=PB得
ΔPAB是等腰三角形,
进而想到“三线合一”
C
探究新知 2
线段的垂直平分线的判定
如果一个点到线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上。
已知:如图,线段AB,
求证:
A
B
P
PA=PB
点P在AB的垂直平分线上.
∵PA=PB
∴△PAB是等腰三角形
取AB中点C,连接PC
∴ AC=BC且PC⊥AB
即PC垂直平分AB
∴点P在AB的垂直平分线上
证明
(2):
分析:
由PA=PB得
ΔPAB是等腰三角形,
进而想到“三线合一”
C
想一想: 若作出∠P的角平分线,结论是否也可以得证?
探究新知 2
线段的垂直平分线的判定
线段垂直平分线的判定定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
∵ PA=PB
∴点P在AB的垂直平分线上
几何语言:
A
C
B
P
M
N
(到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上).
1.经过线段的中点,并且垂直于这条线段的直线
是线段的垂直平分线。
探究新知 2
线段的垂直平分线的判定
(定义判定)
2.到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
(判定定理)
【 例2】在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,
求证: AO垂直平分线段BC.
探究新知 2
线段的垂直平分线的判定
证明:延长AO交BC于点D,
方法 在△ABO和△ACO中,
(1) AB = AC
OB = OC
AO = AO
∴△ABO≌△ACO
∴∠BAO=∠CAO
∵ AB = AC
∴BD=CD且AD ⊥BC
∴直线 AO 是线段 BC 的垂直平分线
D
定义判定
【 例2】在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,
求证: AO垂直平分线段BC.
探究新知 2
线段的垂直平分线的判定
证明: ∵ AB=AC
方法 ∴ 点A在BC的垂直平分线上
(2) ∵ OB=OC
∴点O在BC的垂直平分线上
∴ 直线AO垂直平分BC
判定定理
要证明一条直线为线段的垂直平分线,
需要证明两个点在这条线段的垂直平分线上。
巩固练习:如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过D作AB的垂线交AC于点E,CD交BE于点F, 求证:EB垂直平分线段CD.
探究新知 2
线段的垂直平分线的判定
分析:证明EB垂直平分CD 即判定直线EB为垂直平分线,
定义判定 和判定定理判定这两种方法中,你打算选哪种判定方法呢?
证明: ∵ED⊥AB
∴∠EDB=90°
∵∠ECB=90°
在Rt△EDB≌Rt△ECB
EB=EB
DB=CB
∴Rt△EDB≌Rt△ECB(HL)
∴∠1=∠2
又∵BD=BC
∴BF⊥CD且DF=CF
∴EB垂直平分线段CD
1
2
定义判定
巩固练习:如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过D作AB的垂线交AC于点E,CD交BE于点F, 求证:EB垂直平分线段CD.
探究新知 2
线段的垂直平分线的判定
分析:证明EB垂直平分CD 即判定直线EB为垂直平分线,
定义判定 和判定定理判定这两种方法中,你打算选哪种判定方法呢?
证明: ∵ED⊥AB
∴∠EDB=90°
∵∠ECB=90°
在Rt△EDB≌Rt△ECB
EB=EB
DB=CB
∴Rt△EDB≌Rt△ECB(HL)
∴ ED=EC
∴ 点E在BC的垂直平分线上
∵ BD=BC
∴ 点B在BC的垂直平分线上
即EB垂直平分线段CD
判定定理
巩固练习:如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过D作AB的垂线交AC于点E,CD交BE于点F, 求证:EB垂直平分线段CD.
探究新知 2
线段的垂直平分线的判定
分析:证明EB垂直平分CD 即判定直线EB为垂直平分线,
定义判定 和判定定理判定这两种方法中,你打算选哪种判定方法呢?
证明: ∵ BD=BC
∴∠3=∠4
∵ED⊥AB
∴∠EDB=90°
∵∠ECB=90°
∴ 90°- ∠3= 90°- ∠4
即∠5=∠6
∴ ED=EC
∴ 点E在BC的垂直平分线上
∵ BD=BC
∴ 点B在BC的垂直平分线上
即EB垂直平分线段CD
判定定理
3
4
5
6
课堂小结
1.经过线段的中点,并且垂直于这条线段的直线
是线段的垂直平分线。
2.到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。
课堂小结
1.垂直、平分
2.线段垂直平分线上的点到这条线段两端的距离相等。
线段的
垂直平分线
性质
判定
当堂检测
当堂检测
1.如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B,D,C,E
在同一条直线上,则AB+DB与DE之间的关系是( )
A.AB+DB>DE B.AB+DB<DE C.AB+DB=DE D.非上述答案
?
2.如图,在暑假期间,某学校对其校内的高中楼(图中的点A),临建楼(图中的点B)和图书馆
(图中的点C)进行装修,装修工人小明需要放置一批装修物资,使得装修物资到点A,点B 和点C
的距离相等,则装修物资应该放置在( )
A.AC、BC两边高线的交点处
B.在AC、BC两边中线的交点处
C.在AC、BC两边垂直平分线的交点处
D.在∠A、∠B两内角平分线的交点处
C
C
谢谢大家再见
北师大版数学八年级下册第一章第三节
学习目标
1.证明线段垂直平分线的性质定理及其逆命题。
2.灵活运用线段垂直平分线的有关知识进行证明或计算.
学习目标
探究新知
线段的垂直平分线
定义:经过线段的中点,并且垂直于这条线段的直线是线段的垂直平分线。
A
C
B
l
性质
判定
几何图形
线段的垂直平分线
1.垂直、平分
探究新知 1
线段的垂直平分线的性质
2.线段垂直平分线上的点到这条线段两端的距离相等
问题1:线段的垂直平分线有哪些性质?
(定义)
问题2:你能证明这个结论吗?
A
C
B
l
探究新知 1
线段的垂直平分线的性质
证明命题:线段垂直平分线上的点到这条线段两端的距离相等
已知:如图,直线l ⊥ AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
P
A
B
l
C
证明:∵l ⊥ AB
∴ ∠ PCA= ∠ PCB=90°
在 ΔPAC和Δ PBC中
AC=BC
∠ PCA= ∠ PCB
PC=PC
∴ ΔPAC ≌Δ PBC
∴PA=PB
探究新知 1
线段的垂直平分线的性质
线段垂直平分线的性质定理:
线段垂直平分线上的点到这条线段两端的距离相等。
∵MN⊥AB,AC=BC
∴PA=PB
几何语言:
A
C
B
P
M
N
∴∠A=∠B
这条定理常用来证明两条线段或两个角相等
(线段垂直平分线上的点到
这条线段两个端点距离相等).
(等边对等角).
常用辅助线:给出线段垂直平分线上的点,将它与线段两端点连接起来
∴∠A=∠B
A
C
B
l
探究新知 1
线段的垂直平分线的性质
【例1】在△ABC 中,AB、AC 的垂直平分线相交于点O,分别交BC边于点M、N,连接AM,AN.
(1)若△AMN的周长为6,求BC的长;
(2)若∠MON=50°,求∠MAN的度数。
解:(1)∵M在AB的垂直平分线上
∴MA=MB
同理,NA=NC
∵△AMN的周长为6
∴MA+MN+NA=6
∴ BC= MB+MN+NC=6
(2)∵ MA=MB
∴∠1=∠B
同理, ∠2=∠C
∵∠MON=50°,OM ⊥AB, ON ⊥AC
∴∠BAC=360 °-90 °-90 °-50 °=130°
即∠1+ ∠MAN + ∠2=130°
1
2
又∵ ∠B+ ∠BAC + ∠C=180°
∴∠B+ ∠1+ ∠MAN + ∠2 + ∠C=180°
即2∠1+ ∠MAN + 2∠2=180°
∴∠1+ ∠2 =50°
∴∠MAN=130°﹣50°=80°
①
②
1.经过线段的中点,并且垂直于这条线段的直线是线段的垂直平分线。
探究新知 2
线段的垂直平分线的判定
2.
问题3:线段的垂直平分线有哪些判定方法?
(定义判定)
问题4:你能写出垂直平分线性质定理的逆命题吗?
?
性质定理的逆命题
?
探究新知 2
线段的垂直平分线的判定
性质定理(原命题):
如果一个点是线段垂直平分线上的点,那么这个点到这条线段两个端点的距离相等。
逆命题:
如果一个点到线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上。
问题5:这个逆命题是真命题吗?你能证明它吗?
探究新知 2
线段的垂直平分线的判定
证明逆命题:如果一个点到线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上。
已知:如图,线段AB,
求证:
A
B
P
PA=PB
点P在AB的垂直平分线上.
∵PA=PB
∴△PAB是等腰三角形
过点P作PC⊥AB,垂足为点C
∴ AC=BC
即PC垂直平分AB
∴点P在AB的垂直平分线上
证明
(1):
分析:
由PA=PB得
ΔPAB是等腰三角形,
进而想到“三线合一”
C
探究新知 2
线段的垂直平分线的判定
如果一个点到线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上。
已知:如图,线段AB,
求证:
A
B
P
PA=PB
点P在AB的垂直平分线上.
∵PA=PB
∴△PAB是等腰三角形
取AB中点C,连接PC
∴ AC=BC且PC⊥AB
即PC垂直平分AB
∴点P在AB的垂直平分线上
证明
(2):
分析:
由PA=PB得
ΔPAB是等腰三角形,
进而想到“三线合一”
C
想一想: 若作出∠P的角平分线,结论是否也可以得证?
探究新知 2
线段的垂直平分线的判定
线段垂直平分线的判定定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
∵ PA=PB
∴点P在AB的垂直平分线上
几何语言:
A
C
B
P
M
N
(到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上).
1.经过线段的中点,并且垂直于这条线段的直线
是线段的垂直平分线。
探究新知 2
线段的垂直平分线的判定
(定义判定)
2.到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
(判定定理)
【 例2】在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,
求证: AO垂直平分线段BC.
探究新知 2
线段的垂直平分线的判定
证明:延长AO交BC于点D,
方法 在△ABO和△ACO中,
(1) AB = AC
OB = OC
AO = AO
∴△ABO≌△ACO
∴∠BAO=∠CAO
∵ AB = AC
∴BD=CD且AD ⊥BC
∴直线 AO 是线段 BC 的垂直平分线
D
定义判定
【 例2】在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,
求证: AO垂直平分线段BC.
探究新知 2
线段的垂直平分线的判定
证明: ∵ AB=AC
方法 ∴ 点A在BC的垂直平分线上
(2) ∵ OB=OC
∴点O在BC的垂直平分线上
∴ 直线AO垂直平分BC
判定定理
要证明一条直线为线段的垂直平分线,
需要证明两个点在这条线段的垂直平分线上。
巩固练习:如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过D作AB的垂线交AC于点E,CD交BE于点F, 求证:EB垂直平分线段CD.
探究新知 2
线段的垂直平分线的判定
分析:证明EB垂直平分CD 即判定直线EB为垂直平分线,
定义判定 和判定定理判定这两种方法中,你打算选哪种判定方法呢?
证明: ∵ED⊥AB
∴∠EDB=90°
∵∠ECB=90°
在Rt△EDB≌Rt△ECB
EB=EB
DB=CB
∴Rt△EDB≌Rt△ECB(HL)
∴∠1=∠2
又∵BD=BC
∴BF⊥CD且DF=CF
∴EB垂直平分线段CD
1
2
定义判定
巩固练习:如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过D作AB的垂线交AC于点E,CD交BE于点F, 求证:EB垂直平分线段CD.
探究新知 2
线段的垂直平分线的判定
分析:证明EB垂直平分CD 即判定直线EB为垂直平分线,
定义判定 和判定定理判定这两种方法中,你打算选哪种判定方法呢?
证明: ∵ED⊥AB
∴∠EDB=90°
∵∠ECB=90°
在Rt△EDB≌Rt△ECB
EB=EB
DB=CB
∴Rt△EDB≌Rt△ECB(HL)
∴ ED=EC
∴ 点E在BC的垂直平分线上
∵ BD=BC
∴ 点B在BC的垂直平分线上
即EB垂直平分线段CD
判定定理
巩固练习:如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过D作AB的垂线交AC于点E,CD交BE于点F, 求证:EB垂直平分线段CD.
探究新知 2
线段的垂直平分线的判定
分析:证明EB垂直平分CD 即判定直线EB为垂直平分线,
定义判定 和判定定理判定这两种方法中,你打算选哪种判定方法呢?
证明: ∵ BD=BC
∴∠3=∠4
∵ED⊥AB
∴∠EDB=90°
∵∠ECB=90°
∴ 90°- ∠3= 90°- ∠4
即∠5=∠6
∴ ED=EC
∴ 点E在BC的垂直平分线上
∵ BD=BC
∴ 点B在BC的垂直平分线上
即EB垂直平分线段CD
判定定理
3
4
5
6
课堂小结
1.经过线段的中点,并且垂直于这条线段的直线
是线段的垂直平分线。
2.到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。
课堂小结
1.垂直、平分
2.线段垂直平分线上的点到这条线段两端的距离相等。
线段的
垂直平分线
性质
判定
当堂检测
当堂检测
1.如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B,D,C,E
在同一条直线上,则AB+DB与DE之间的关系是( )
A.AB+DB>DE B.AB+DB<DE C.AB+DB=DE D.非上述答案
?
2.如图,在暑假期间,某学校对其校内的高中楼(图中的点A),临建楼(图中的点B)和图书馆
(图中的点C)进行装修,装修工人小明需要放置一批装修物资,使得装修物资到点A,点B 和点C
的距离相等,则装修物资应该放置在( )
A.AC、BC两边高线的交点处
B.在AC、BC两边中线的交点处
C.在AC、BC两边垂直平分线的交点处
D.在∠A、∠B两内角平分线的交点处
C
C
谢谢大家再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
