北师大版八年级数学下册6.1平行四边形的性质课件(共29张PPT)
文档属性
| 名称 | 北师大版八年级数学下册6.1平行四边形的性质课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 910.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 10:50:49 | ||
图片预览


文档简介
回顾迎新
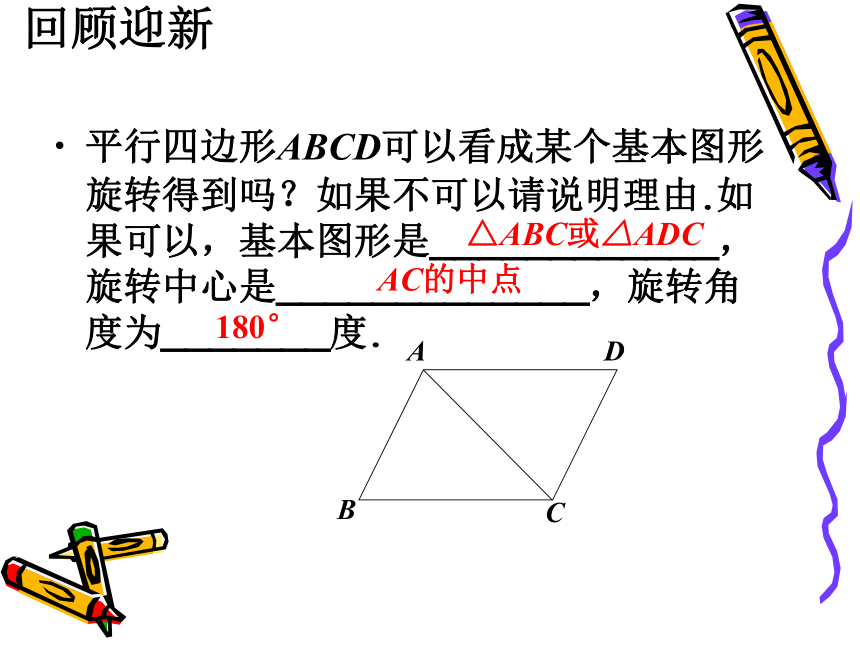
平行四边形ABCD可以看成某个基本图形旋转得到吗?如果不可以请说明理由.如果可以,基本图形是____________,旋转中心是_____________,旋转角度为_______度.
A
B
C
D
△ABC或△ADC
AC的中点
180°
A
B
C
D
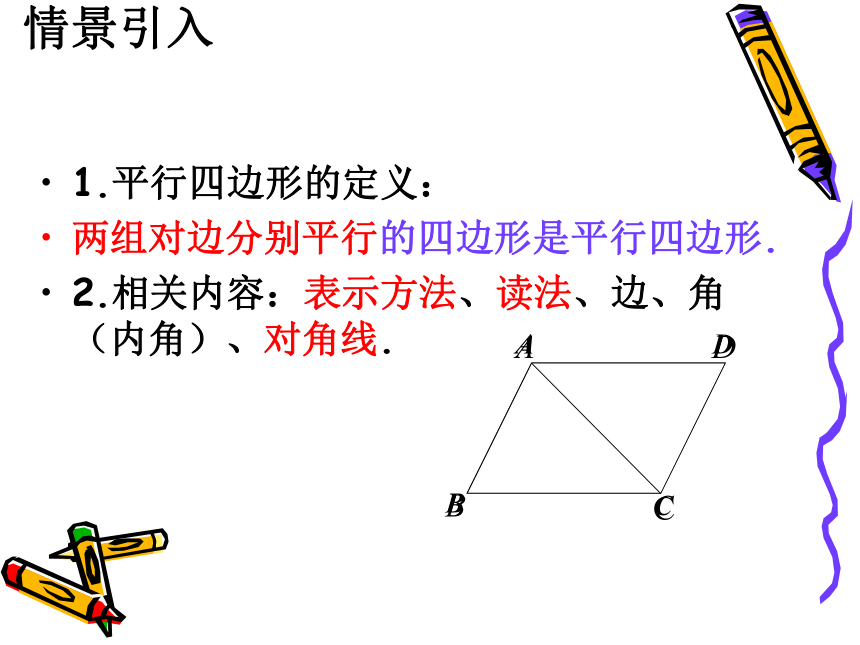
1.平行四边形的定义:
两组对边分别平行的四边形是平行四边形.
2.相关内容:表示方法、读法、边、角(内角)、对角线.
情景引入
A
B
C
D
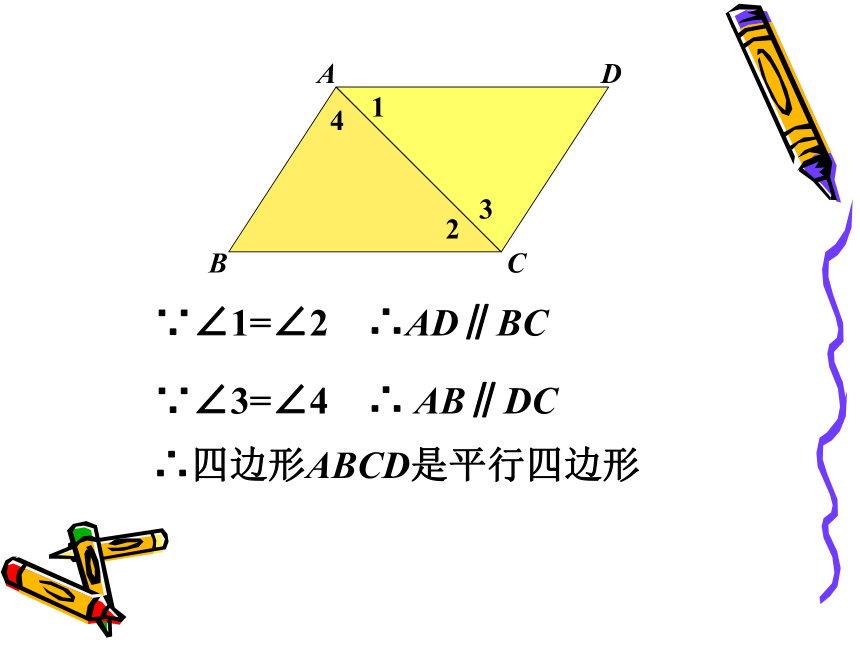
∵∠1=∠2 ∴AD∥BC
D
C
B
A
1
2
3
4
∵∠3=∠4 ∴ AB∥DC
∴四边形ABCD是平行四边形
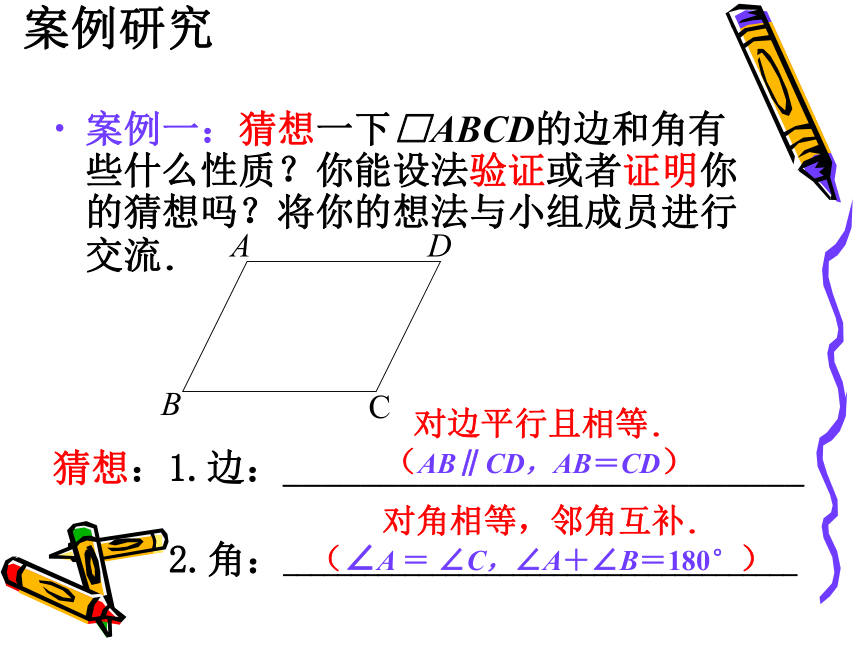
案例一:猜想一下□ABCD的边和角有些什么性质?你能设法验证或者证明你的猜想吗?将你的想法与小组成员进行交流.
案例研究
A
B
C
D
猜想:1.边:___________________________
2.角:______________________________________
对边平行且相等.
(AB∥CD,AB=CD)
对角相等,邻角互补.
(∠A = ∠C,∠A+∠B=180°)
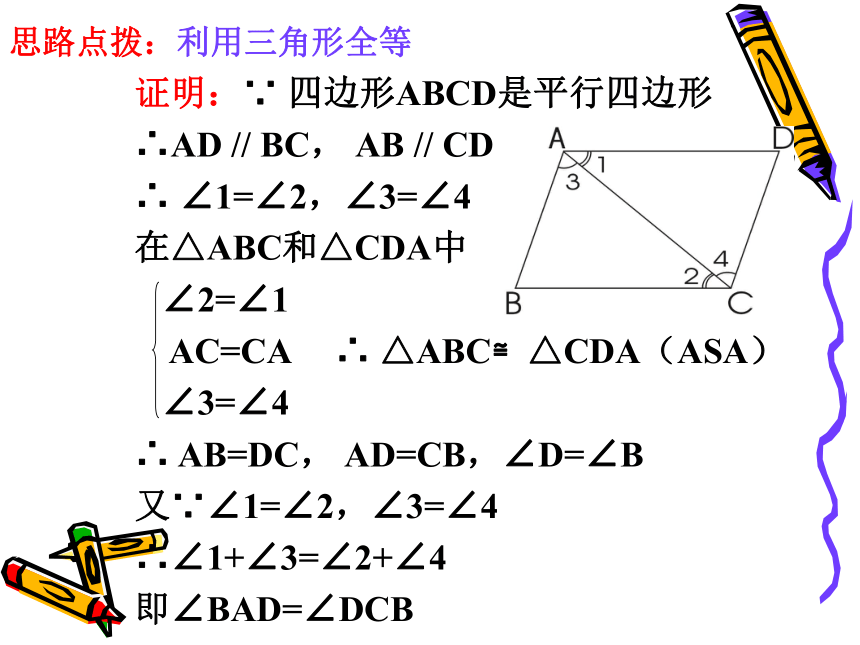
证明:∵ 四边形ABCD是平行四边形
∴AD // BC, AB // CD
∴ ∠1=∠2,∠3=∠4
在△ABC和△CDA中
∠2=∠1
AC=CA ∴ △ABC≌△CDA(ASA)
∠3=∠4
∴ AB=DC, AD=CB,∠D=∠B
又∵∠1=∠2,∠3=∠4
∴∠1+∠3=∠2+∠4
即∠BAD=∠DCB
思路点拨:利用三角形全等
思考:利用平行四边形的性质给你的小组成员提个问题.
A
B
C
D
训练:1. 在□ABCD中,AB=3,BC=5,
则AD= ,CD= .
2. 在□ABCD中,∠B=56°,
则∠A= ,∠C= ,∠D= .
3. 已知□ABCD的周长为40cm,
△ABC周长为25,则对角线
AC=( )cm.
A.5 B.15 C.6 D.16
5
3
124°
56°
124°
A
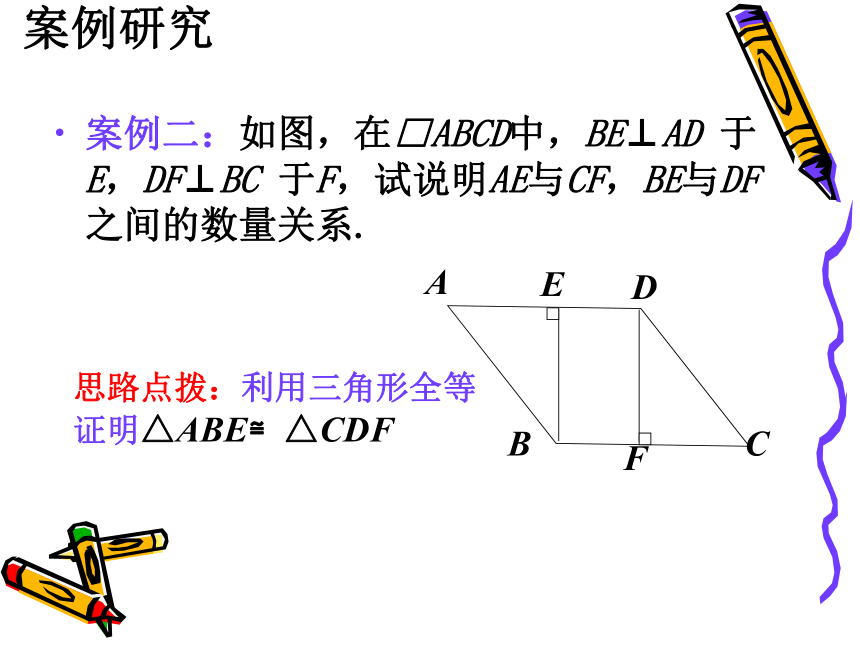
案例二:如图,在□ABCD中,BE⊥AD 于E,DF⊥BC 于F,试说明AE与CF,BE与DF之间的数量关系.
案例研究
A
B
C
D
E
F
思路点拨:利用三角形全等
证明△ABE≌△CDF
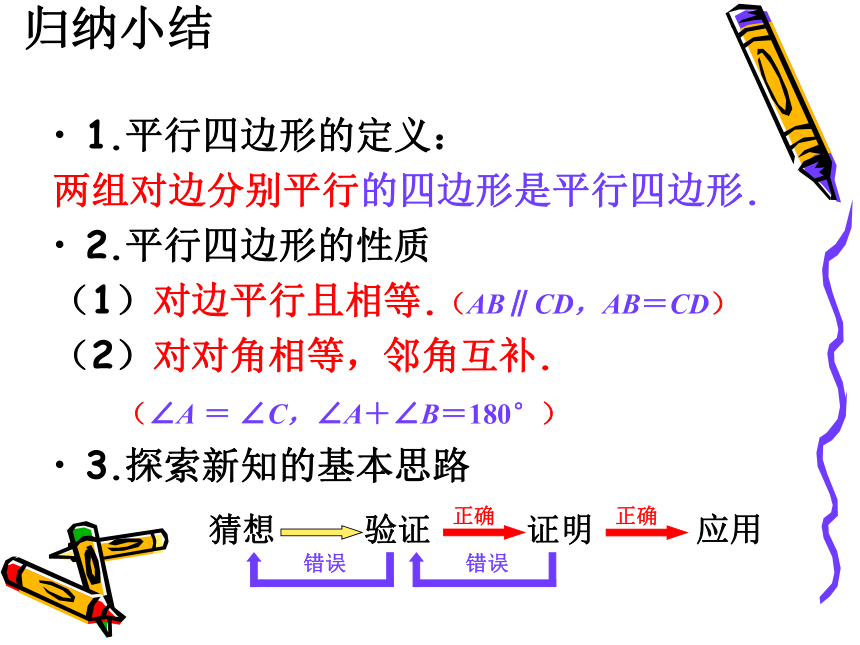
1.平行四边形的定义:
两组对边分别平行的四边形是平行四边形.
2.平行四边形的性质
(1)对边平行且相等.(AB∥CD,AB=CD)
(2)对对角相等,邻角互补.
(∠A = ∠C,∠A+∠B=180°)
3.探索新知的基本思路
归纳小结
猜想
验证
证明
正确
正确
应用
错误
错误
2.上节课我们掌握了平行四边
形的哪些性质?
1.什么是平行四边形?
复习回顾
1.定义:
有两组对边分别平行的四边形
叫做平行四边形。
记作:
ABCD
读作:平行四边形ABCD
A
B
C
D
复习回顾
2.平行四边形的性质:
平行四边形的对边相等.
平行四边形的对角相等。
对边:
对角:
∵四边形ABCD是平行四边形,
∴∠A=∠C , ∠B=∠D.
复习回顾
∵四边形ABCD是平行四边形,
∴AB=CD , AD=BC.
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
大毛
二毛
三毛
四毛
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
一、教学目标:
1.理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质.
2.能综合运用平行四边形的性质解决平行四边形的有关计算问题,和简单的证明题.
3.培养学生的推理论证能力和逻辑思维能力.
???????
二、重点、难点
1.重点:平行四边形对角线互相平分的性质,以及性质的应用.
2.难点:综合运用平行四边形的性质进行有关的论证和计算.
教学目标:
1、理解平行四边形中心对称的特征,掌握平行四
边形对角线互相平分的性质;
2、能综合运用平行四边形的性质解决有关平行四
边形的计算问题,和简单的证明题。
3、培养学生推理能力和逻辑思维能力。
教学重点:平行四边形对角线互相平分的性质和性质的
简单运用。
教学难点:综合运用平行四边形的性质进行有关的计算
和论证。
A
C
D
B
如图, ABCD的对角线AC、BD相交于点O.
O
猜一猜:
线段OA与OC、OB与OD长度有何关系?
●
量一量:
A
B
D
C
O
A
B
D
C
O
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
●
A
D
O
C
B
D
B
O
C
A
再看一遍
●
A
D
O
C
B
D
B
O
C
A
你有什么猜想?
结论
●
ABCD绕它的中心O旋转180°后与自身重合,这时我们说 ABCD是 中心对称图形,点O叫对称中心。
平行四边形的对角线互相平分.
●
你能证明 它吗?
根据刚才的旋转,你知道平行四边形的对角线有什么性质吗?
猜一猜
A
C
D
B
O
已知:如图: ABCD的对角线AC、BD
相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠3,∠2=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
3
2
1
平行四边形的对角线互相平分.
4
平行四边形的性质:
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
A
D
B
C
O
A
C
D
B
O
●
大毛
四毛
三毛
二毛
M
1、在 ABCD中,AC与BD相交于点O,AC=30cm,BD=24cm,
那么AO=_____Bo=____。若AB=18cm,则三角形COD的周长=___.
2、如图所示,在 ABCD中,AC与BD相交与点O,如果AC=
16,BD=10,AB=x,则x取值范围是_______。若AB=12 BC=6,则OA的取值范围是________.
3、若平行四边形的一边长为5,则它的两条对角线长可以
是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
A
B
C
D
15cm
12cm
o
45cm
33D
小试牛刀
O
D
B
A
C
4、如图,在 ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,
则CD=______.
5
5、选择:平行四边形具有而一般四边形不具有 的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
B
选一选
6、如图,已知平行四边形ABCD的周长等于86cm,对角线AC
与BD相交于点0,三角形AOB的周长比三角形BOC的周长大
13cm,则AB=_______ BC=_______CD=_______ AD=_______
7、平行四边形ABCD中,对角线AC与BD相交与点0,图中相等
的线段有_____________________________若平行四边形ABCD
中,AB=2AD,三角形AOB的周长比三角形AOD的周长大3cm,则
平行四边形ABCD的周长=_________。
A
B
C
D
O
28cm
15cm
15
15cm
28cm
AB=CD AD=BC OA=OC OB=OD
18cm
1、 通过本节课的学习,你有什么收获?
2、 平行四边形的性质共有哪些?
边:
角:
对角线:
对边平行,对边相等
对角相等,邻角互补
对角线互相平分
平行四边形ABCD可以看成某个基本图形旋转得到吗?如果不可以请说明理由.如果可以,基本图形是____________,旋转中心是_____________,旋转角度为_______度.
A
B
C
D
△ABC或△ADC
AC的中点
180°
A
B
C
D
1.平行四边形的定义:
两组对边分别平行的四边形是平行四边形.
2.相关内容:表示方法、读法、边、角(内角)、对角线.
情景引入
A
B
C
D
∵∠1=∠2 ∴AD∥BC
D
C
B
A
1
2
3
4
∵∠3=∠4 ∴ AB∥DC
∴四边形ABCD是平行四边形
案例一:猜想一下□ABCD的边和角有些什么性质?你能设法验证或者证明你的猜想吗?将你的想法与小组成员进行交流.
案例研究
A
B
C
D
猜想:1.边:___________________________
2.角:______________________________________
对边平行且相等.
(AB∥CD,AB=CD)
对角相等,邻角互补.
(∠A = ∠C,∠A+∠B=180°)
证明:∵ 四边形ABCD是平行四边形
∴AD // BC, AB // CD
∴ ∠1=∠2,∠3=∠4
在△ABC和△CDA中
∠2=∠1
AC=CA ∴ △ABC≌△CDA(ASA)
∠3=∠4
∴ AB=DC, AD=CB,∠D=∠B
又∵∠1=∠2,∠3=∠4
∴∠1+∠3=∠2+∠4
即∠BAD=∠DCB
思路点拨:利用三角形全等
思考:利用平行四边形的性质给你的小组成员提个问题.
A
B
C
D
训练:1. 在□ABCD中,AB=3,BC=5,
则AD= ,CD= .
2. 在□ABCD中,∠B=56°,
则∠A= ,∠C= ,∠D= .
3. 已知□ABCD的周长为40cm,
△ABC周长为25,则对角线
AC=( )cm.
A.5 B.15 C.6 D.16
5
3
124°
56°
124°
A
案例二:如图,在□ABCD中,BE⊥AD 于E,DF⊥BC 于F,试说明AE与CF,BE与DF之间的数量关系.
案例研究
A
B
C
D
E
F
思路点拨:利用三角形全等
证明△ABE≌△CDF
1.平行四边形的定义:
两组对边分别平行的四边形是平行四边形.
2.平行四边形的性质
(1)对边平行且相等.(AB∥CD,AB=CD)
(2)对对角相等,邻角互补.
(∠A = ∠C,∠A+∠B=180°)
3.探索新知的基本思路
归纳小结
猜想
验证
证明
正确
正确
应用
错误
错误
2.上节课我们掌握了平行四边
形的哪些性质?
1.什么是平行四边形?
复习回顾
1.定义:
有两组对边分别平行的四边形
叫做平行四边形。
记作:
ABCD
读作:平行四边形ABCD
A
B
C
D
复习回顾
2.平行四边形的性质:
平行四边形的对边相等.
平行四边形的对角相等。
对边:
对角:
∵四边形ABCD是平行四边形,
∴∠A=∠C , ∠B=∠D.
复习回顾
∵四边形ABCD是平行四边形,
∴AB=CD , AD=BC.
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
大毛
二毛
三毛
四毛
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
一、教学目标:
1.理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质.
2.能综合运用平行四边形的性质解决平行四边形的有关计算问题,和简单的证明题.
3.培养学生的推理论证能力和逻辑思维能力.
???????
二、重点、难点
1.重点:平行四边形对角线互相平分的性质,以及性质的应用.
2.难点:综合运用平行四边形的性质进行有关的论证和计算.
教学目标:
1、理解平行四边形中心对称的特征,掌握平行四
边形对角线互相平分的性质;
2、能综合运用平行四边形的性质解决有关平行四
边形的计算问题,和简单的证明题。
3、培养学生推理能力和逻辑思维能力。
教学重点:平行四边形对角线互相平分的性质和性质的
简单运用。
教学难点:综合运用平行四边形的性质进行有关的计算
和论证。
A
C
D
B
如图, ABCD的对角线AC、BD相交于点O.
O
猜一猜:
线段OA与OC、OB与OD长度有何关系?
●
量一量:
A
B
D
C
O
A
B
D
C
O
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
●
A
D
O
C
B
D
B
O
C
A
再看一遍
●
A
D
O
C
B
D
B
O
C
A
你有什么猜想?
结论
●
ABCD绕它的中心O旋转180°后与自身重合,这时我们说 ABCD是 中心对称图形,点O叫对称中心。
平行四边形的对角线互相平分.
●
你能证明 它吗?
根据刚才的旋转,你知道平行四边形的对角线有什么性质吗?
猜一猜
A
C
D
B
O
已知:如图: ABCD的对角线AC、BD
相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠3,∠2=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
3
2
1
平行四边形的对角线互相平分.
4
平行四边形的性质:
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
A
D
B
C
O
A
C
D
B
O
●
大毛
四毛
三毛
二毛
M
1、在 ABCD中,AC与BD相交于点O,AC=30cm,BD=24cm,
那么AO=_____Bo=____。若AB=18cm,则三角形COD的周长=___.
2、如图所示,在 ABCD中,AC与BD相交与点O,如果AC=
16,BD=10,AB=x,则x取值范围是_______。若AB=12 BC=6,则OA的取值范围是________.
3、若平行四边形的一边长为5,则它的两条对角线长可以
是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
A
B
C
D
15cm
12cm
o
45cm
3
小试牛刀
O
D
B
A
C
4、如图,在 ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,
则CD=______.
5
5、选择:平行四边形具有而一般四边形不具有 的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
B
选一选
6、如图,已知平行四边形ABCD的周长等于86cm,对角线AC
与BD相交于点0,三角形AOB的周长比三角形BOC的周长大
13cm,则AB=_______ BC=_______CD=_______ AD=_______
7、平行四边形ABCD中,对角线AC与BD相交与点0,图中相等
的线段有_____________________________若平行四边形ABCD
中,AB=2AD,三角形AOB的周长比三角形AOD的周长大3cm,则
平行四边形ABCD的周长=_________。
A
B
C
D
O
28cm
15cm
15
15cm
28cm
AB=CD AD=BC OA=OC OB=OD
18cm
1、 通过本节课的学习,你有什么收获?
2、 平行四边形的性质共有哪些?
边:
角:
对角线:
对边平行,对边相等
对角相等,邻角互补
对角线互相平分
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
