北师大版八年级数学下册第6章第1节平行四边形的性质课件(共43张PPT)
文档属性
| 名称 | 北师大版八年级数学下册第6章第1节平行四边形的性质课件(共43张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 10:53:34 | ||
图片预览








文档简介
6.1平行四边形的性质
第 1课时
“哪里有数学,哪里就有美!”
——古希腊数学家普洛克拉斯
欣赏图片—引入新课
有没有你熟悉的图形
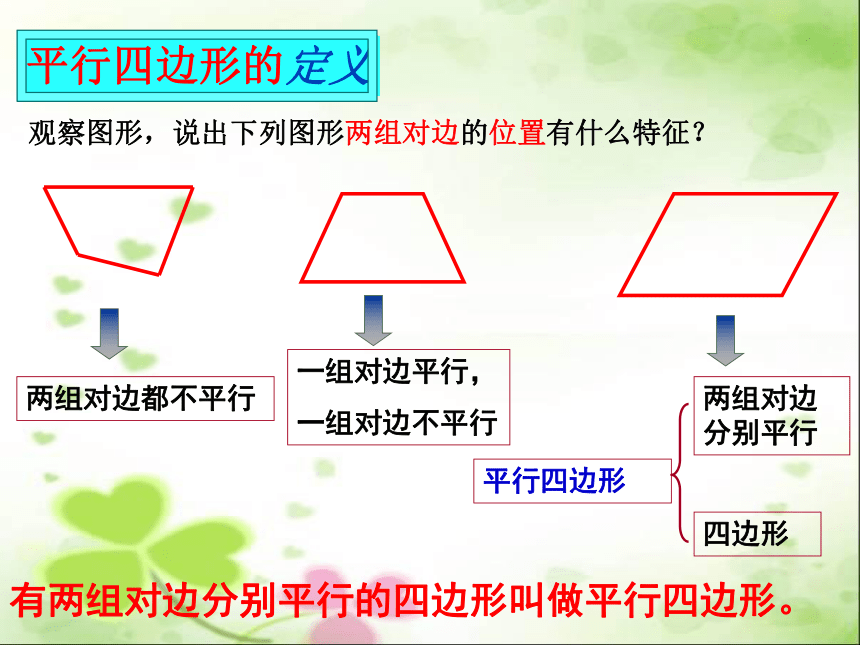
直观感知—得出概念
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
有两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形两组对边的位置有什么特征?
平行四边形的定义
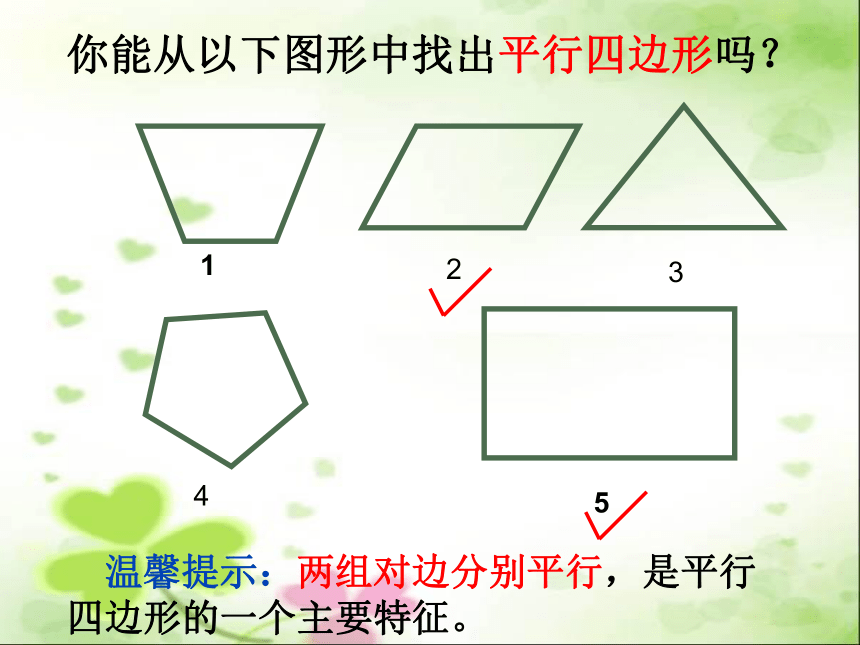
你能从以下图形中找出平行四边形吗?
温馨提示:两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
平行四边形 相对的边称为 对边
相邻的边称为 邻边
如图:线段AC、BD就是 ABCD的对角线
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形
记作: ABCD (顺序)
读作:平行四边形ABCD
平行四边形 相对的角称为 对角
相邻的角称为 邻角
平行四边形的相关概念
可采取度量、平移、旋转、折叠、拼图等方法探究平行四边形的对称性以及边、角的数量关系。
小组活动
实践探索—发现性质
一探:平行四边形的对称性
请同学们拿出你准备的两个全等的平行四边 形,然后研究下面的问题:
1.平行四边形是轴对称图形吗?如果是,请找出对称轴,如果不是,请说明理由.
2.平行四边形是中心对称图形吗?如果是,请找出对称中心,如果不是,请说明理由.
3.你能验证你的猜想吗?
结论1:平行四边形是中心对称图形,
两条对角线的交点是它的对称中心
通过下面的操作,你能否发现平行四边形的对边、对角、邻角还有哪些性质?
二探:平行四边形边、角的性质
结论2:平行四边形对边平行且相等;
平行四边形对角相等;
平行四边形 邻角互补;
平行四边形性质
推理论证—验证性质
你能证明它们吗?
平行四边形的对边相等;
平行四边形的对角相等。
一证:平行四边形的对边相等
已知:如图,四边形ABCD是平行四边形.
求证: AB=CD,BC=DA.
A
B
C
D
3
4
2
1
证明:连接AC.
∵四边形ABCD为平行四边形(已知),
∴AB∥CD,BC∥DA (平行四边形对边平行) .
∴∠1=∠2,∠3=∠4(两直线平行,内错角相等) .
∵AC=CA(公共边),
∴△ABC≌△CDA(AAS).
∴AB=CD,BC=DA(全等三角形的对应边相等).
B
C
D
A
二证:平行四边形的对角相等
已知:如图,四边形ABCD是平行四边形.
求证:∠B=∠D,∠A=∠C
A
B
C
D
证明:∵ 四边形ABCD是平行四边形(已知),
∴ AD // BC, AB // CD (平行四边形的定义).
∴ ∠A+∠B =180°
∠A+∠D =180°(两直线平行,同旁内角互补).
∴ ∠B =∠D (同角的补角相等) .
同理可证:∠A =∠C.
平行四边形的性质
A
B
C
D
文字语言
几何语言
对边平行
AB∥DC ,AD∥BC
对边相等
AB=DC ,AD=BC
邻角互补
∠A+∠B =180°……
边
角
∠A=∠C ,∠B=∠D
对角相等
温馨提示:这些性质为证明(或解决)线段相等、角相等提供了新的理论依据
1、在 ABCD中,已知∠A=130°,则∠B= ,
∠C= ,∠D= ;
A 组
50°
130°
50°
A
B
C
D
2、在 ABCD中,AD=30,CD=25,则AB=_____
BC= ;
25
30
学以致用—运用性质
② 若∠A、∠B的度数之比为5∶4,则∠C= ,
∠D= ;
B 组
27
9
100°
80°
100°
80°
1、已知 ABCD的周长是72cm,若AB∶BC=1∶3,
则BC=____ cm,CD=_____ cm;
2、在 ABCD中,
① 若∠A+∠C=200°,则∠A= ,∠B= ;
A
B
C
D
C 组
例题讲解
如图,在 ABCD中,E、F是对角线AC上的两点,且AE=CF.
求证:BE=DF .
E
A
F
D
C
B
评价反思—归纳小结
通过本节课的学习,你有哪些收获? 还有哪些疑惑?(与同伴交流分享)
两组对边分别平行的四边形叫做平行四边形。
中心对称图形
对边相等
对边平行
对角相等
邻角互补
平行四边形
定义:
性质
边
角
第六章 平行四边形
2.上节课我们掌握了平行四边
形的哪些性质?
1.什么是平行四边形?
1.定义:
有两组对边分别平行的四边形
叫做平行四边形。
2.记作:
ABCD
3.读作:平行四边形ABCD
A
B
C
D
平行四边形的性质:
平行四边形的对边相等.
平行四边形的对角相等。
1.对边:
2.对角:
∵四边形ABCD是平行四边形,
∴∠A=∠C , ∠B=∠D.
∵四边形ABCD是平行四边形,
∴AB=CD , AD=BC.
●
A
D
O
C
B
D
B
O
C
A
看一看
上节课我们知道了平行四边形是中心对称图形。对称中心是什么?
你发现了什么?
ABCD绕它的中心O旋转180°后与自身重
合,此时,OA=OC,OB=OD.
平行四边形的对角线互相平分.
●
你能证明 它吗?
根据刚才的旋转,你知道平行四边形的对角线有什么性质吗?
A
C
D
B
O
已知:如图: ABCD的对角线AC、BD
相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
3
2
4
1
求证:平行四边形的对角线互相平分.
平行四边形的性质
几何语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
A
D
B
C
O
平行四边形的对角线互相平分.
例2,如图, ABCD中,对角线AC、BD交于点O,过点0的直线与AD,BC分别相交于点E、F。
求证:OE=OF.
证明:∵四边形ABCD是平行四边形
∴OB=OD(平行四边形的对角线互相平分)
AD∥BC(平行四边形的定义)
∴∠ODE=∠OBF
∵∠DOE=∠BOF
∴△DOE≌△BOF
∴OE=OF.
B
C
D
A
E
F
O
已知:如图, ABCD的对角线AC、BD相交于
点O. ∠ADB=90°,OA=3,OB=6.
求:AD和AC的长度。
做一做
A
C
D
B
O
1.选择:平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
B
2. 若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
O
D
B
A
C
D
3.如图,在平面直角坐标系中, OBCD的顶点
O﹑B﹑D的坐标如图所示,则顶点C的
坐标为( )
x
Y
C
O (0,0)
B(5,0)
D(2,3)
A. (3,7) B. (5,3)
C. (7,3) D. (8,2)
C
4.如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是 _________.
O
D
B
A
C
●
1<AD<9
O
D
B
A
C
5.如图,在 ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,
则CD=______.
5
6. ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系?并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
3
4
7.如图,在 ABCD中,
BC=10cm, AC=8cm,
BD=14cm,
(1)△ AOD的周长是多少?为什么?
( 2) △ ABC与△ DBC的周长哪个长?长多少?
A
B
D
C
O
1. 通过本节课的学习,你有什么收获?
2. 平行四边形的性质共有哪些?
边:
角:
对角线:
第 1课时
“哪里有数学,哪里就有美!”
——古希腊数学家普洛克拉斯
欣赏图片—引入新课
有没有你熟悉的图形
直观感知—得出概念
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
有两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形两组对边的位置有什么特征?
平行四边形的定义
你能从以下图形中找出平行四边形吗?
温馨提示:两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
平行四边形 相对的边称为 对边
相邻的边称为 邻边
如图:线段AC、BD就是 ABCD的对角线
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形
记作: ABCD (顺序)
读作:平行四边形ABCD
平行四边形 相对的角称为 对角
相邻的角称为 邻角
平行四边形的相关概念
可采取度量、平移、旋转、折叠、拼图等方法探究平行四边形的对称性以及边、角的数量关系。
小组活动
实践探索—发现性质
一探:平行四边形的对称性
请同学们拿出你准备的两个全等的平行四边 形,然后研究下面的问题:
1.平行四边形是轴对称图形吗?如果是,请找出对称轴,如果不是,请说明理由.
2.平行四边形是中心对称图形吗?如果是,请找出对称中心,如果不是,请说明理由.
3.你能验证你的猜想吗?
结论1:平行四边形是中心对称图形,
两条对角线的交点是它的对称中心
通过下面的操作,你能否发现平行四边形的对边、对角、邻角还有哪些性质?
二探:平行四边形边、角的性质
结论2:平行四边形对边平行且相等;
平行四边形对角相等;
平行四边形 邻角互补;
平行四边形性质
推理论证—验证性质
你能证明它们吗?
平行四边形的对边相等;
平行四边形的对角相等。
一证:平行四边形的对边相等
已知:如图,四边形ABCD是平行四边形.
求证: AB=CD,BC=DA.
A
B
C
D
3
4
2
1
证明:连接AC.
∵四边形ABCD为平行四边形(已知),
∴AB∥CD,BC∥DA (平行四边形对边平行) .
∴∠1=∠2,∠3=∠4(两直线平行,内错角相等) .
∵AC=CA(公共边),
∴△ABC≌△CDA(AAS).
∴AB=CD,BC=DA(全等三角形的对应边相等).
B
C
D
A
二证:平行四边形的对角相等
已知:如图,四边形ABCD是平行四边形.
求证:∠B=∠D,∠A=∠C
A
B
C
D
证明:∵ 四边形ABCD是平行四边形(已知),
∴ AD // BC, AB // CD (平行四边形的定义).
∴ ∠A+∠B =180°
∠A+∠D =180°(两直线平行,同旁内角互补).
∴ ∠B =∠D (同角的补角相等) .
同理可证:∠A =∠C.
平行四边形的性质
A
B
C
D
文字语言
几何语言
对边平行
AB∥DC ,AD∥BC
对边相等
AB=DC ,AD=BC
邻角互补
∠A+∠B =180°……
边
角
∠A=∠C ,∠B=∠D
对角相等
温馨提示:这些性质为证明(或解决)线段相等、角相等提供了新的理论依据
1、在 ABCD中,已知∠A=130°,则∠B= ,
∠C= ,∠D= ;
A 组
50°
130°
50°
A
B
C
D
2、在 ABCD中,AD=30,CD=25,则AB=_____
BC= ;
25
30
学以致用—运用性质
② 若∠A、∠B的度数之比为5∶4,则∠C= ,
∠D= ;
B 组
27
9
100°
80°
100°
80°
1、已知 ABCD的周长是72cm,若AB∶BC=1∶3,
则BC=____ cm,CD=_____ cm;
2、在 ABCD中,
① 若∠A+∠C=200°,则∠A= ,∠B= ;
A
B
C
D
C 组
例题讲解
如图,在 ABCD中,E、F是对角线AC上的两点,且AE=CF.
求证:BE=DF .
E
A
F
D
C
B
评价反思—归纳小结
通过本节课的学习,你有哪些收获? 还有哪些疑惑?(与同伴交流分享)
两组对边分别平行的四边形叫做平行四边形。
中心对称图形
对边相等
对边平行
对角相等
邻角互补
平行四边形
定义:
性质
边
角
第六章 平行四边形
2.上节课我们掌握了平行四边
形的哪些性质?
1.什么是平行四边形?
1.定义:
有两组对边分别平行的四边形
叫做平行四边形。
2.记作:
ABCD
3.读作:平行四边形ABCD
A
B
C
D
平行四边形的性质:
平行四边形的对边相等.
平行四边形的对角相等。
1.对边:
2.对角:
∵四边形ABCD是平行四边形,
∴∠A=∠C , ∠B=∠D.
∵四边形ABCD是平行四边形,
∴AB=CD , AD=BC.
●
A
D
O
C
B
D
B
O
C
A
看一看
上节课我们知道了平行四边形是中心对称图形。对称中心是什么?
你发现了什么?
ABCD绕它的中心O旋转180°后与自身重
合,此时,OA=OC,OB=OD.
平行四边形的对角线互相平分.
●
你能证明 它吗?
根据刚才的旋转,你知道平行四边形的对角线有什么性质吗?
A
C
D
B
O
已知:如图: ABCD的对角线AC、BD
相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
3
2
4
1
求证:平行四边形的对角线互相平分.
平行四边形的性质
几何语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
A
D
B
C
O
平行四边形的对角线互相平分.
例2,如图, ABCD中,对角线AC、BD交于点O,过点0的直线与AD,BC分别相交于点E、F。
求证:OE=OF.
证明:∵四边形ABCD是平行四边形
∴OB=OD(平行四边形的对角线互相平分)
AD∥BC(平行四边形的定义)
∴∠ODE=∠OBF
∵∠DOE=∠BOF
∴△DOE≌△BOF
∴OE=OF.
B
C
D
A
E
F
O
已知:如图, ABCD的对角线AC、BD相交于
点O. ∠ADB=90°,OA=3,OB=6.
求:AD和AC的长度。
做一做
A
C
D
B
O
1.选择:平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
B
2. 若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
O
D
B
A
C
D
3.如图,在平面直角坐标系中, OBCD的顶点
O﹑B﹑D的坐标如图所示,则顶点C的
坐标为( )
x
Y
C
O (0,0)
B(5,0)
D(2,3)
A. (3,7) B. (5,3)
C. (7,3) D. (8,2)
C
4.如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是 _________.
O
D
B
A
C
●
1<AD<9
O
D
B
A
C
5.如图,在 ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,
则CD=______.
5
6. ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系?并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
3
4
7.如图,在 ABCD中,
BC=10cm, AC=8cm,
BD=14cm,
(1)△ AOD的周长是多少?为什么?
( 2) △ ABC与△ DBC的周长哪个长?长多少?
A
B
D
C
O
1. 通过本节课的学习,你有什么收获?
2. 平行四边形的性质共有哪些?
边:
角:
对角线:
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
