北师大版八年级数学下册6.2平行四边形的判定 第1课时 教学课件(共19张PPT)
文档属性
| 名称 | 北师大版八年级数学下册6.2平行四边形的判定 第1课时 教学课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 149.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 00:00:00 | ||
图片预览





文档简介
6.2 平行四边形的判定
第1课时
第六章 平行四边形
一、 学习目标
1.经历平行四边形的判别定理的探索过程,发展学生的合情推理的能力.
2. 探索并证明平行四边形的判别定理,发展学生的演绎推理的能力.
1.平行四边形的定义是什么?
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质有哪些?
(1)平行四边形的对边相等.
(2)平行四边形的对角相等.
(3)平行四边形的对角线互相平分.
二、 复习导入
3.大家思考下如何判定一个四边形是平行四边形呢?
二、 复习导入
两对长度分别相等的木条,能否在平面内用这四根木条拼成一个平行四边形.
三、 探究新知
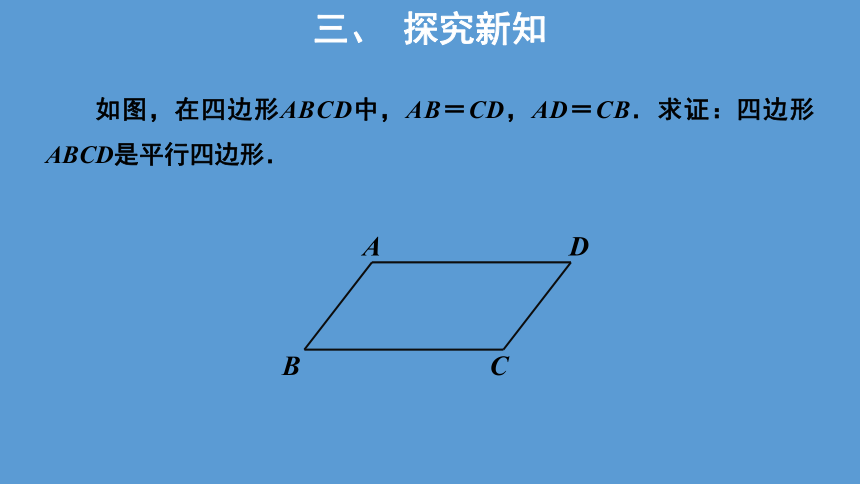
如图,在四边形ABCD中,AB=CD,AD=CB.求证:四边形ABCD是平行四边形.
D
C
B
A
三、 探究新知
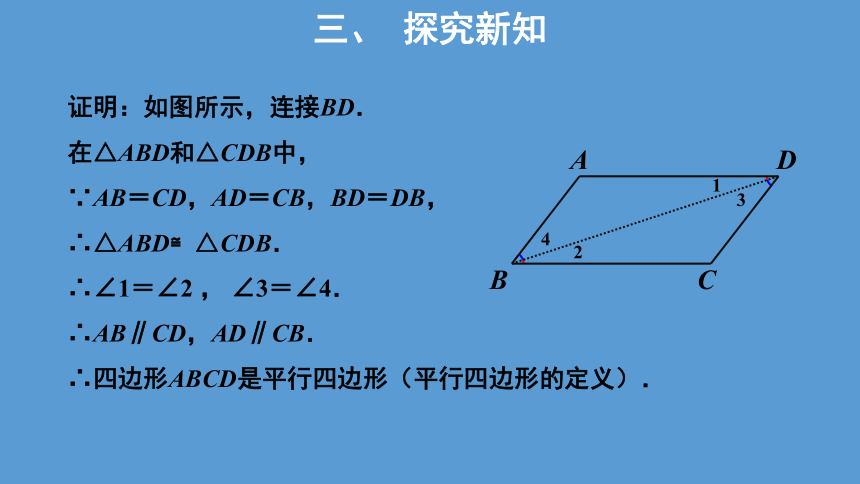
证明:如图所示,连接BD.
在△ABD和△CDB中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2 , ∠3=∠4.
∴AB∥CD,AD∥CB.
∴四边形ABCD是平行四边形(平行四边形的定义).
D
C
B
A
1
3
2
4
三、 探究新知
定理:两组对边分别相等的四边形是平行四边形.
三、 探究新知
利用两块全等三角形的七色板拼接四边形.
三、 探究新知
如图,在四边形ABCD中,AB∥CD,且AB=CD.求证:四边形ABCD是平行四边形.
D
C
B
A
三、 探究新知
证明:如图,连接AC.
∵AB∥CD,
∴∠BAC=∠ACD,
又∵ AB=CD,AC=CA,
∴ △BAC≌△DCA,
∴ BC=AD.
∴ 四边形ABCD是平行四边形.
(4)
D
C
B
A
三、 探究新知
定理:一组对边平行且相等的四边形是平行四边形.
三、 探究新知
例1.已知:如图,在□ABCD中,点E,F分别在AB和CD上,BE=DF.
求证:四边形AECF是平行四边形.
F
E
D
C
B
A
四、 典例精讲
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
又∵BE=DF,
∴AF=EC,AF∥EC,
∴四边形AECF是平行四边形
(一组对边平行且相等的四边形是平行四边形).
F
E
D
C
B
A
四、 典例精讲
1.能判定四边形ABCD为平行四边形的题设是( )
A.AB∥CD,AD=BC
B.AB=CD,AD=BC
C.∠A=∠B,∠C=∠D
D.AB=AD,CB=CD
B
五、 课堂练习
2.下列叙述正确的的有( )
①对角线互相垂直的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③一组对边平行,另一组对边相等的四边形是平行四边形.
A.3个 B.2个 C.1个 D.0个
C
五、 课堂练习
3.在四边形ABCD中,AD=8cm,AB=4cm.当BC=______cm,CD=______cm 时,四边形ABCD为平行四边形.
4.在四边形ABCD中,AD=BC,BD为对角线,∠ADB=∠CBD,则AB和CD的关系为_________.
8
4
相等
五、 课堂练习
1.判定一个四边形是平行四边形的方法有哪几种?这些方法是从什么角度去考虑的?
2.我们是通过什么方法得出平行四边形的这几种判定方法的,这样的探索过程对你有什么启发?
3.类比、观察、拼图、实验等都是学习数学、发现结论的常用方法.
六、 课堂小结
再见
第1课时
第六章 平行四边形
一、 学习目标
1.经历平行四边形的判别定理的探索过程,发展学生的合情推理的能力.
2. 探索并证明平行四边形的判别定理,发展学生的演绎推理的能力.
1.平行四边形的定义是什么?
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质有哪些?
(1)平行四边形的对边相等.
(2)平行四边形的对角相等.
(3)平行四边形的对角线互相平分.
二、 复习导入
3.大家思考下如何判定一个四边形是平行四边形呢?
二、 复习导入
两对长度分别相等的木条,能否在平面内用这四根木条拼成一个平行四边形.
三、 探究新知
如图,在四边形ABCD中,AB=CD,AD=CB.求证:四边形ABCD是平行四边形.
D
C
B
A
三、 探究新知
证明:如图所示,连接BD.
在△ABD和△CDB中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2 , ∠3=∠4.
∴AB∥CD,AD∥CB.
∴四边形ABCD是平行四边形(平行四边形的定义).
D
C
B
A
1
3
2
4
三、 探究新知
定理:两组对边分别相等的四边形是平行四边形.
三、 探究新知
利用两块全等三角形的七色板拼接四边形.
三、 探究新知
如图,在四边形ABCD中,AB∥CD,且AB=CD.求证:四边形ABCD是平行四边形.
D
C
B
A
三、 探究新知
证明:如图,连接AC.
∵AB∥CD,
∴∠BAC=∠ACD,
又∵ AB=CD,AC=CA,
∴ △BAC≌△DCA,
∴ BC=AD.
∴ 四边形ABCD是平行四边形.
(4)
D
C
B
A
三、 探究新知
定理:一组对边平行且相等的四边形是平行四边形.
三、 探究新知
例1.已知:如图,在□ABCD中,点E,F分别在AB和CD上,BE=DF.
求证:四边形AECF是平行四边形.
F
E
D
C
B
A
四、 典例精讲
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
又∵BE=DF,
∴AF=EC,AF∥EC,
∴四边形AECF是平行四边形
(一组对边平行且相等的四边形是平行四边形).
F
E
D
C
B
A
四、 典例精讲
1.能判定四边形ABCD为平行四边形的题设是( )
A.AB∥CD,AD=BC
B.AB=CD,AD=BC
C.∠A=∠B,∠C=∠D
D.AB=AD,CB=CD
B
五、 课堂练习
2.下列叙述正确的的有( )
①对角线互相垂直的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③一组对边平行,另一组对边相等的四边形是平行四边形.
A.3个 B.2个 C.1个 D.0个
C
五、 课堂练习
3.在四边形ABCD中,AD=8cm,AB=4cm.当BC=______cm,CD=______cm 时,四边形ABCD为平行四边形.
4.在四边形ABCD中,AD=BC,BD为对角线,∠ADB=∠CBD,则AB和CD的关系为_________.
8
4
相等
五、 课堂练习
1.判定一个四边形是平行四边形的方法有哪几种?这些方法是从什么角度去考虑的?
2.我们是通过什么方法得出平行四边形的这几种判定方法的,这样的探索过程对你有什么启发?
3.类比、观察、拼图、实验等都是学习数学、发现结论的常用方法.
六、 课堂小结
再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
