北师大版八年级下册数学课件:3.1 图形的平移第3课时--直角坐标系中图形的两次平移与坐标的变化(共22张PPT)
文档属性
| 名称 | 北师大版八年级下册数学课件:3.1 图形的平移第3课时--直角坐标系中图形的两次平移与坐标的变化(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 13:02:37 | ||
图片预览






文档简介
(共22张PPT)
7 8
x
y
0
2
1
1
2
-1
-2
3
4
5
-3
3
4
5
6
知识与技能:
进一步体会图形的平移与坐标变化之间的关系。
过程与方法:
在探究图形的平移与坐标变化关系的过程中,体会知识的形成过程及数形结合的方法,积累数学经验。
情感与态度:
通过观察生活中“平移”的实例,感受“生活中处处有数学”,激发学生学习数学的兴趣;通过学生欣赏、设计平移图案,使学生感受数学美。
5
x
y
-2
0
-1
1
2
-1
-2
3
4
5
-3
1
2
3
4
-3
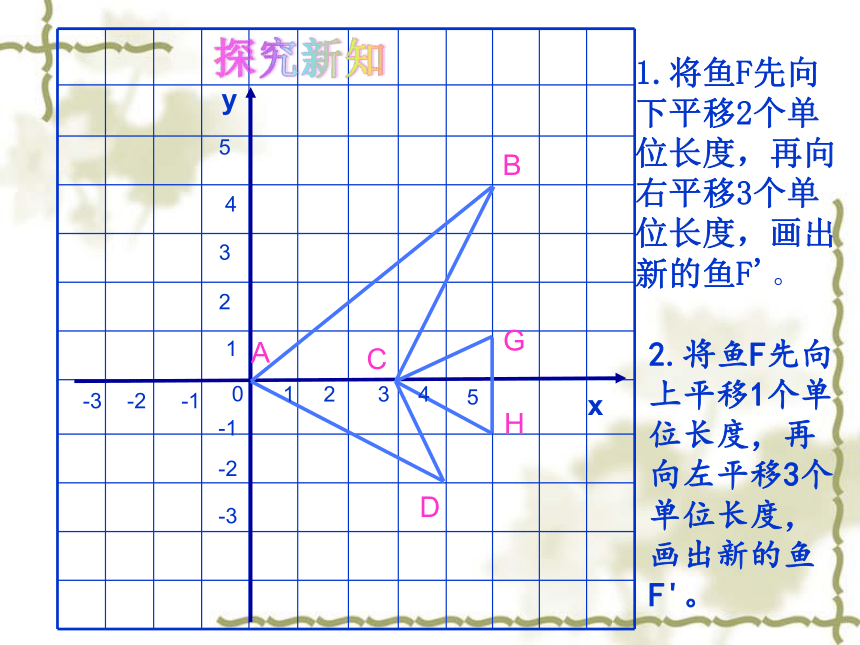
2.将鱼F先向上平移1个单位长度,再向左平移3个单位长度,画出新的鱼F'。
B
A
C
D
G
H
1.将鱼F先向
下平移2个单
位长度,再向右平移3个单
位长度,画出新的鱼F'。
7 8
x
y
0
2
1
1
2
-1
-2
3
4
5
-3
3
4
5
6
A
A1
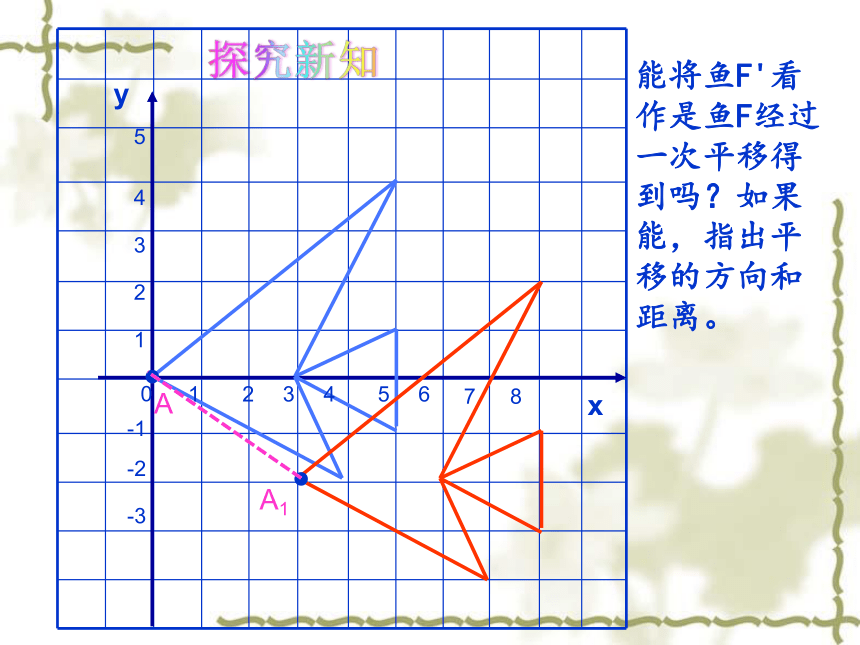
能将鱼F'看作是鱼F经过一次平移得到吗?如果能,指出平移的方向和距离。
5
x
y
-2
0
-1
1
2
-1
-2
3
4
5
-3
1
2
3
4
-3
A1
A
能将鱼F'看作
是鱼F经过一次
平移得到吗?
如果能,指出
平移的方向和
距离。
一个图形依次沿 轴方向、 轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的。
在鱼F和鱼F'
中,对应点
的坐标有什
么变化?与
平移有什么
对应关系。
A
B
C
D
G
H
A1
B1
C1
D1
G1
H1
A2
B2
C2
D2
G2
H2
1
2
3
0
4
5
6
7
8
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
5
沿x轴方向平移a(a>0)个单位长度,
再沿y轴方向平移b(b>0)个单位长度。
点(x,y)的平移与点的坐标变化规律:
平移前坐标 平移方向 平移后坐标
(x,y) 先向右再向上
(x,y) 先向右再向下
(x,y) 先向左再向上
(x,y) 先向左再向下
20分
30分
50分
返回
如图,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1),(-3,1),(-1,-1).30 s后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )
A.Q′(2,3),R′(4,1)
B.Q′(2,3),R′(2,1)
C.Q′(2,2),R′(4,1)
D.Q′(3,3),R′(3,1)
A
返回
若把两个直角边长为2cm等腰直角三角形如图重叠放置,再把三角形ABC沿着BC方向平移到三角形A’DC’的位置,则
(1)若平移距离为1,三角形ABC与三角形A’DC’重叠部分的面积( )
(2)若平移距离为X(0≤X≤2),则重叠部分的面积( )
返回
三角形ABC三个顶点的坐标分别为A(0,3),B(-1,0),C(1,0)。小红把 三角形 ABC平移后得到了三角形 A’B’C’,并写出了它的三个顶点的坐标A’(0,0),B’(-2,-3),C’(2,-3) 。
(1)你认为小红所写的三个顶点的坐标正确吗?
(2)如果小红所写的三个顶点的纵坐标都正确,三个顶点的横坐标中只有一个正确,那么你能帮小红正确写出三个顶点的坐标吗?
(1) A'(0,0) B'(-1,-3) C'(1,-3)
(2) A'(-1,0) B'(-2,-3) C'(0,-3)
(3) A'(1,0) B'(0,-3) C'(2,-3)
返回
利用一个基本图形,通过平移作图,设计一个精美的图案。
这节课你有哪些收获?
习题3.3 1,2
7 8
x
y
0
2
1
1
2
-1
-2
3
4
5
-3
3
4
5
6
知识与技能:
进一步体会图形的平移与坐标变化之间的关系。
过程与方法:
在探究图形的平移与坐标变化关系的过程中,体会知识的形成过程及数形结合的方法,积累数学经验。
情感与态度:
通过观察生活中“平移”的实例,感受“生活中处处有数学”,激发学生学习数学的兴趣;通过学生欣赏、设计平移图案,使学生感受数学美。
5
x
y
-2
0
-1
1
2
-1
-2
3
4
5
-3
1
2
3
4
-3
2.将鱼F先向上平移1个单位长度,再向左平移3个单位长度,画出新的鱼F'。
B
A
C
D
G
H
1.将鱼F先向
下平移2个单
位长度,再向右平移3个单
位长度,画出新的鱼F'。
7 8
x
y
0
2
1
1
2
-1
-2
3
4
5
-3
3
4
5
6
A
A1
能将鱼F'看作是鱼F经过一次平移得到吗?如果能,指出平移的方向和距离。
5
x
y
-2
0
-1
1
2
-1
-2
3
4
5
-3
1
2
3
4
-3
A1
A
能将鱼F'看作
是鱼F经过一次
平移得到吗?
如果能,指出
平移的方向和
距离。
一个图形依次沿 轴方向、 轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的。
在鱼F和鱼F'
中,对应点
的坐标有什
么变化?与
平移有什么
对应关系。
A
B
C
D
G
H
A1
B1
C1
D1
G1
H1
A2
B2
C2
D2
G2
H2
1
2
3
0
4
5
6
7
8
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
5
沿x轴方向平移a(a>0)个单位长度,
再沿y轴方向平移b(b>0)个单位长度。
点(x,y)的平移与点的坐标变化规律:
平移前坐标 平移方向 平移后坐标
(x,y) 先向右再向上
(x,y) 先向右再向下
(x,y) 先向左再向上
(x,y) 先向左再向下
20分
30分
50分
返回
如图,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1),(-3,1),(-1,-1).30 s后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )
A.Q′(2,3),R′(4,1)
B.Q′(2,3),R′(2,1)
C.Q′(2,2),R′(4,1)
D.Q′(3,3),R′(3,1)
A
返回
若把两个直角边长为2cm等腰直角三角形如图重叠放置,再把三角形ABC沿着BC方向平移到三角形A’DC’的位置,则
(1)若平移距离为1,三角形ABC与三角形A’DC’重叠部分的面积( )
(2)若平移距离为X(0≤X≤2),则重叠部分的面积( )
返回
三角形ABC三个顶点的坐标分别为A(0,3),B(-1,0),C(1,0)。小红把 三角形 ABC平移后得到了三角形 A’B’C’,并写出了它的三个顶点的坐标A’(0,0),B’(-2,-3),C’(2,-3) 。
(1)你认为小红所写的三个顶点的坐标正确吗?
(2)如果小红所写的三个顶点的纵坐标都正确,三个顶点的横坐标中只有一个正确,那么你能帮小红正确写出三个顶点的坐标吗?
(1) A'(0,0) B'(-1,-3) C'(1,-3)
(2) A'(-1,0) B'(-2,-3) C'(0,-3)
(3) A'(1,0) B'(0,-3) C'(2,-3)
返回
利用一个基本图形,通过平移作图,设计一个精美的图案。
这节课你有哪些收获?
习题3.3 1,2
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
