北师大版九年级上册2.1认识一元二次方程(1)课件(共21张PPT)
文档属性
| 名称 | 北师大版九年级上册2.1认识一元二次方程(1)课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 11:15:40 | ||
图片预览








文档简介
2020
2.1认识一元二次方程(1)
02
01
03
2020
教学目标
经历由具体问题抽象出一元二次方程的概念的过程;
体会方程是刻画现实世界中数量关系的有效模型;
理解一元二次方程及其相关概念.
一、复习回顾
1.什么叫做方程?
2.我们学过哪些方程?
一元一次方程
二元一次方程
分式方程
整式方程
含有未知数的等式.
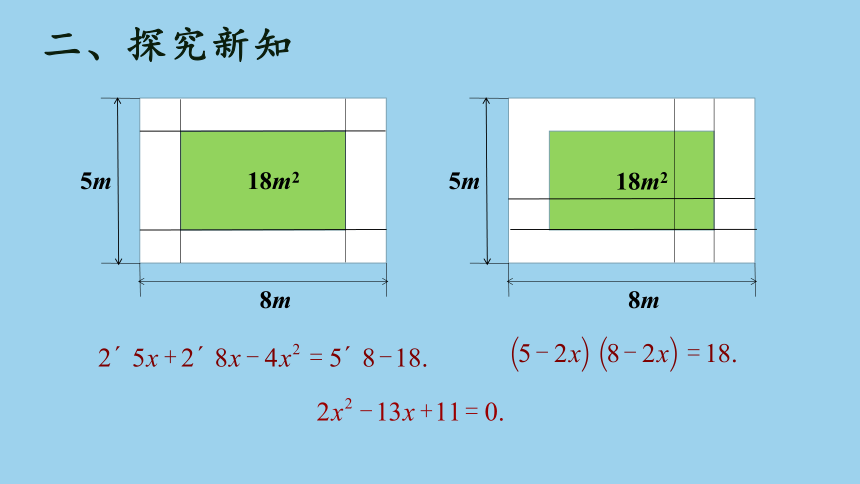
1.如图,幼儿园某教室矩形地面的长为8m,宽为5m,现准备挨地面正中间铺设一块面积为18m2的地毯,四周未铺地毯的条形区域的宽度都相同,求四周未铺地毯的条形区域的宽度是多少?
如果设所求的宽为x米,你能列出怎样的方程?
二、探究新知
8m
5m
18m2
8m
5m
18m2
二、探究新知
2.观察下面的等式:102+112+122=132+142.
你还能找到其他五个连续整数,使前三个数的平方和等于后两个数的平方和吗?如果设这五个连续整数中的第一个为x,那么怎么用x来表示它后面的四个数?你能列出怎样的方程?
解:如果设这五个连续整数中的第一个为x,那么其余四个数依次为:x+1,x+2,x+3,x+4,
根据题意,列出方程:
整理得:
二、探究新知
3.如图所示,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?你能计算出滑动前梯子底端距墙的距离吗?如果设梯子底端滑动xm,你能列出怎样的方程?
C
B
A
根据勾股定理:
根据题意,得:
整理得:
二、探究新知
二、探究新知
观察以下方程有哪些共同特征?
②含未知数项的最高次数是2;
①只含有一个未知数;
③整式方程.
二、探究新知
一元二次方程
的形式,这样的方程叫做一元二次方程.
只含有一个未知数x的整式方程,并且都可以化成
二、探究新知
的形式,这样的方程叫做一元二次方程.
只含有一个未知数x的整式方程,并且都可以化成
一元二次方程
(1)b,c可以为零,也可以不为零;
(2)当a=0,
中二次项不存在.
如何理解
三、典例分析
1.下列方程中是关于x的一元一次方程的是( )
三、典例分析
2.把下列方程化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项:
{D7AC3CCA-C797-4891-BE02-D94E43425B78}方程
一般形式
二次项系数
一次项系数
常数项
化成一般形式后找系数、常数项.
三、典例分析
3.根据题意列出方程:已知直角三角形的三边长为连续整数,求它的三边长.
由勾股定理得:
解:设该直角三角形较长直角边为x,则另外两边为x-1,x+1.
四、随堂练习
1.下列方程中是关于x的一元一次方程的是( )
(1)整式方程;
(2)只含有一个未知数;
(3)含有未知数的项的
最高次数是2.
四、随堂练习
四、随堂练习
四、随堂练习
2.下列方程:① ② ③ ④
⑤ ⑥ 是一元二次方程的有( )
③⑤
①②
②⑥
③④
3.一元一次方程 的一般形式为 ,二次项为 ,二次项系数为 ,一次项为 ,一次项系数为 ,常数项为 .
注意符号!
五、能力提升
1.根据题意,列出一元二次方程:
(1)有一面积为54m2的长方形,将它的一边剪短5m,另一边剪短2m,恰好变成一个正方形,这个正方形的边长是多少?
(2)三个连续整数两两相乘,再求和,结果为242,这三个数分别是多少?
解:(1)设这个正方形的边长为x,则长方形的长为x+5,宽为x+2,
根据题意,得: (x+5)(x+2)=54 即:x2+7x?44=0
(2)设三个连续的整数依次为x,x+1,x+2,
则:x(x+1)+(x+1)(x+2)+x(x+2)=242 即:x2+2x?80=0
五、能力提升
2.从前有一天,一个醉汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺,另一个醉汉教他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了.你知道竹竿有多长吗?
请根据这一问题列出一元二次方程.
解:设竹竿的长为x尺.
由题意得:
(x?4)2+(x?2)2=x2.
即: x2?12x+20=0
五、能力提升
3.若关于x的一元二次方程(m+1)x2+5x+m2?1=0的常数项为0,则m的值等于( )
A. 1 B. ?1 C. ±1 D. 0
A
4.如果关于x的方程 是关于x的一元二次方程,那么m的值为( )
A.±3 B. 3 C. -3 D. 都不对
C
六、课堂小结
一元二次方程的概念
一元二次方程的一般形式
②含未知数项的最高次数是2;
①只含有一个未知数;
③整式方程.
二次项
一次项
常数项
二次项系数
一次项系数
七、布置作业
望同学们能学有所获
2020
2.1认识一元二次方程(1)
02
01
03
2020
教学目标
经历由具体问题抽象出一元二次方程的概念的过程;
体会方程是刻画现实世界中数量关系的有效模型;
理解一元二次方程及其相关概念.
一、复习回顾
1.什么叫做方程?
2.我们学过哪些方程?
一元一次方程
二元一次方程
分式方程
整式方程
含有未知数的等式.
1.如图,幼儿园某教室矩形地面的长为8m,宽为5m,现准备挨地面正中间铺设一块面积为18m2的地毯,四周未铺地毯的条形区域的宽度都相同,求四周未铺地毯的条形区域的宽度是多少?
如果设所求的宽为x米,你能列出怎样的方程?
二、探究新知
8m
5m
18m2
8m
5m
18m2
二、探究新知
2.观察下面的等式:102+112+122=132+142.
你还能找到其他五个连续整数,使前三个数的平方和等于后两个数的平方和吗?如果设这五个连续整数中的第一个为x,那么怎么用x来表示它后面的四个数?你能列出怎样的方程?
解:如果设这五个连续整数中的第一个为x,那么其余四个数依次为:x+1,x+2,x+3,x+4,
根据题意,列出方程:
整理得:
二、探究新知
3.如图所示,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?你能计算出滑动前梯子底端距墙的距离吗?如果设梯子底端滑动xm,你能列出怎样的方程?
C
B
A
根据勾股定理:
根据题意,得:
整理得:
二、探究新知
二、探究新知
观察以下方程有哪些共同特征?
②含未知数项的最高次数是2;
①只含有一个未知数;
③整式方程.
二、探究新知
一元二次方程
的形式,这样的方程叫做一元二次方程.
只含有一个未知数x的整式方程,并且都可以化成
二、探究新知
的形式,这样的方程叫做一元二次方程.
只含有一个未知数x的整式方程,并且都可以化成
一元二次方程
(1)b,c可以为零,也可以不为零;
(2)当a=0,
中二次项不存在.
如何理解
三、典例分析
1.下列方程中是关于x的一元一次方程的是( )
三、典例分析
2.把下列方程化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项:
{D7AC3CCA-C797-4891-BE02-D94E43425B78}方程
一般形式
二次项系数
一次项系数
常数项
化成一般形式后找系数、常数项.
三、典例分析
3.根据题意列出方程:已知直角三角形的三边长为连续整数,求它的三边长.
由勾股定理得:
解:设该直角三角形较长直角边为x,则另外两边为x-1,x+1.
四、随堂练习
1.下列方程中是关于x的一元一次方程的是( )
(1)整式方程;
(2)只含有一个未知数;
(3)含有未知数的项的
最高次数是2.
四、随堂练习
四、随堂练习
四、随堂练习
2.下列方程:① ② ③ ④
⑤ ⑥ 是一元二次方程的有( )
③⑤
①②
②⑥
③④
3.一元一次方程 的一般形式为 ,二次项为 ,二次项系数为 ,一次项为 ,一次项系数为 ,常数项为 .
注意符号!
五、能力提升
1.根据题意,列出一元二次方程:
(1)有一面积为54m2的长方形,将它的一边剪短5m,另一边剪短2m,恰好变成一个正方形,这个正方形的边长是多少?
(2)三个连续整数两两相乘,再求和,结果为242,这三个数分别是多少?
解:(1)设这个正方形的边长为x,则长方形的长为x+5,宽为x+2,
根据题意,得: (x+5)(x+2)=54 即:x2+7x?44=0
(2)设三个连续的整数依次为x,x+1,x+2,
则:x(x+1)+(x+1)(x+2)+x(x+2)=242 即:x2+2x?80=0
五、能力提升
2.从前有一天,一个醉汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺,另一个醉汉教他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了.你知道竹竿有多长吗?
请根据这一问题列出一元二次方程.
解:设竹竿的长为x尺.
由题意得:
(x?4)2+(x?2)2=x2.
即: x2?12x+20=0
五、能力提升
3.若关于x的一元二次方程(m+1)x2+5x+m2?1=0的常数项为0,则m的值等于( )
A. 1 B. ?1 C. ±1 D. 0
A
4.如果关于x的方程 是关于x的一元二次方程,那么m的值为( )
A.±3 B. 3 C. -3 D. 都不对
C
六、课堂小结
一元二次方程的概念
一元二次方程的一般形式
②含未知数项的最高次数是2;
①只含有一个未知数;
③整式方程.
二次项
一次项
常数项
二次项系数
一次项系数
七、布置作业
望同学们能学有所获
2020
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
