北师大版七年级数学下册第四单元4.1认识三角形课件(一)(共34张PPT)
文档属性
| 名称 | 北师大版七年级数学下册第四单元4.1认识三角形课件(一)(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 13:18:11 | ||
图片预览









文档简介
2、观察房屋屋顶的框架你能从中看出4个不同的三角形?
在小学我们探究了三角形三个内角的和等于180? ,你还记得这个结论的探索过程吗?
3.如图,已知∠B=40°,∠C=59°,
∠DEC=47°,则∠F=——
课外能力延伸:如图,将一张三角形纸片ABC沿DE折叠,使点A落到A′处,试说明∠A、∠1、∠2之间的数量关系
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
七 年 级 数 学
下册第四章
在这些优美的画面中,这些物体的侧面都是什么几何图形?
说一说:在日常生活中,还有
哪些三角形形状的物体。
学习目标
1、理解三角形及有关的概念,能用符号
语言表示三角形.
2、探索并证明三角形内角和等于180°,
3、会按角将三角形进行分类,能发现直角 三角形中两个锐角的关系.
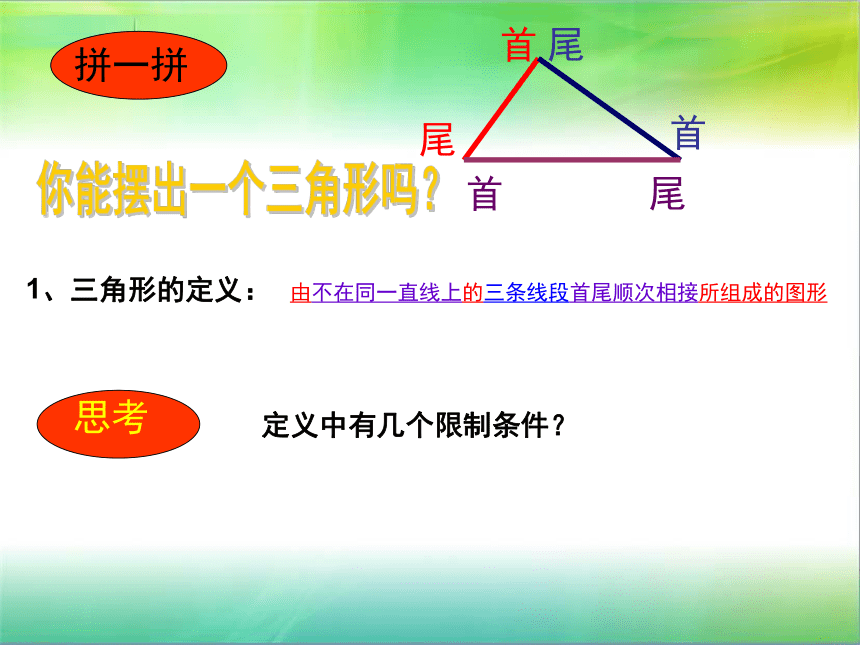
1、三角形的定义:
首
尾
尾
首
尾
首
思考
定义中有几个限制条件?
由不在同一直线上的三条线段首尾顺次相接所组成的图形
拼一拼
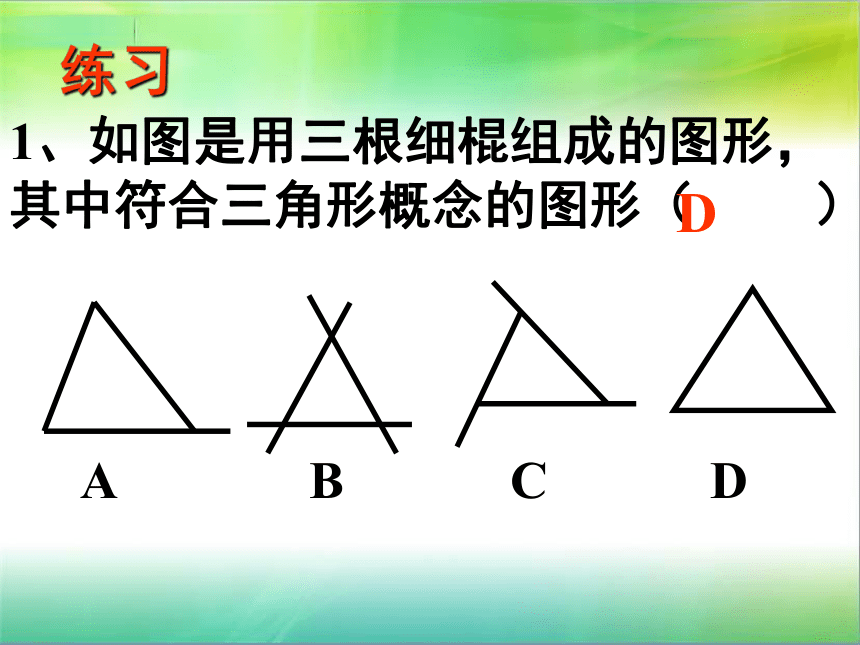
1、如图是用三根细棍组成的图形, 其中符合三角形概念的图形( )
D
A
C
B
D
练习
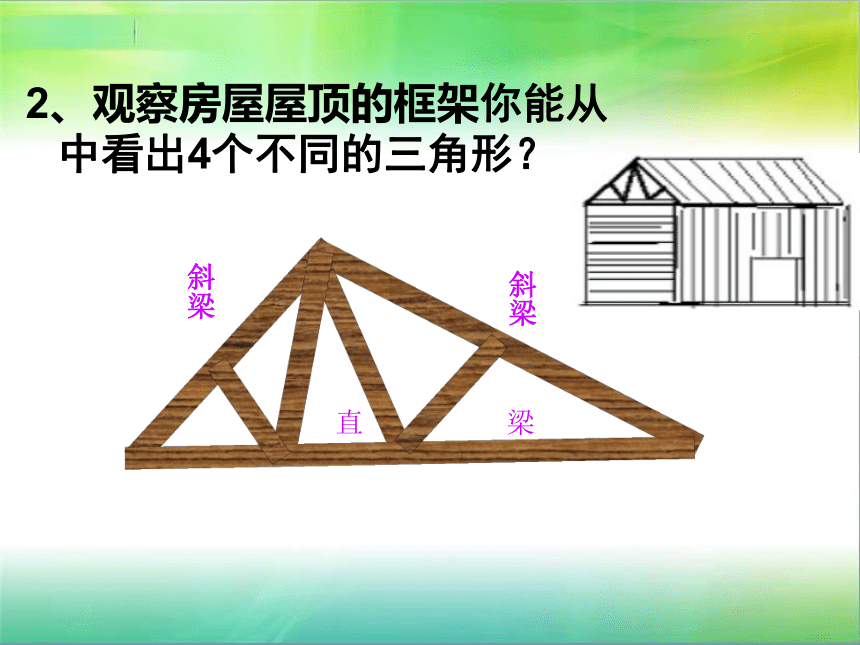
斜梁
斜梁
直 梁
自学指导一:
认真看课本P81第二自然段的做一做以前的
内容。2分钟
重点看:
1、三角形的表示方法及其各部分的名称。
2、写出角的对边及边的对角。
(一)三角形的三要素:
边:
如图三角形中三边 AB、BC、AC。
顶点A所对的边BC也可表示为a,
顶点B所对的边AC也可表示为b ,
顶点C所对的边AB也可表示为c
角:
三角形中有三个角:
顶点:
三角形中有三个顶点:
∠B 的对边是_____
AC
∠A的对边是_____
∠C的对边是_____
BC
AB
∠A,∠B,∠C
顶点A,顶点B,顶点C
A
B
C
c
b
a
AC的对角是_____ BC的对角是_____ AB的对角是_____
∠B
∠A
∠C
一、三角形的相关概念:
A
B
C
记法:
三角形符号“△”,
如:上图的三角形记作:△ABC (或△ BCA或△ CBA 等)
注意: 顶点字母没有限定次序。
(二)如何表示三角形?
例、(1)图中以BC为边的三角形共有______个; 它们分别______________________________.
(2)在△ABD中, ∠ABD是____边的对角,
(3)∠BEC是△_______的内角
D
B
E
C
F
A
4
△BCF; △BCE; △BCD; △BCA
AD
BEC
三角形的三个内角有什么关系?
1
A
B
D
2
C
如图,当时我们是撕下两个角,把∠A移到了∠1的位置,把∠B移到了∠2的位置,三个角合在一起构成了一个平角.
如果只撕下三角形的一个角,你也能得到上面的结论吗?
讨论:如果只撕下三角形的一个角,能
不能得到三角形内角和等于180°?
认真看课本P81做一做
时间4分钟
利用准备好的三角形撕下一个角摆一摆,怎样摆那个撕下的角?才能得到三角形的内角和等于180°
摆出撕下的∠1,让∠1与∠2的顶点重合, ∠1一条边与∠2一边重合.
⌒
1
2
⌒
⌒
3
a
b
⌒
4
思考: ∠1的另一条边b与∠3边a是平行的吗?为什么?
你能得到∠1+ ∠2+∠3=180°请写出来
A
B
C
E
通过刚才的活动,给我们的启示:也可以直接过三角形的一 个顶点作平行线,也能证明三角形的内角和等于180°
已知:△A B C.
求证:∠A +∠B +∠C =180°
A
B
C
E
证明:延长BC到D过C作C E∥B A.
∵CE ∥B A
∴∠A= ∠ACE, ∠B=∠ECD
∵∠BCA+∠ACE+∠ECD=180°
∴ ∠BCA+∠A+∠B= 180°
------------
D
1、在△ABC中,
∠B=100?,∠A=∠C,则∠C=_______度;
40
2、 如图,已知∠B=10,∠C= 20°
∠BOC=110°求∠A的度数
解:延长OC至AB相交得点D
∵ ∠BOC+∠BOD= 180° ∠BOC=110°
∴∠BOD=70 °
∵ ∠BOD+∠BDO+∠B=180°∠B=10 °
∴∠BDO=100 °
∴∠ODA=80°
∵∠C+∠A+∠ODA=180 °
∴∠A=80 °
D
猜一猜
(1)下图中小明所拿三角形被遮住的两个内角是什么角?小颖的
呢?试着说明理由.
(2)下图中三角形被遮住的两个内角可能是什么角?将所
得结果与(1)的结果进行比较.
认真看课本P84练习以前的内容,时间3分钟。思考下列问题
1、三角形按角怎么分?
2、什么叫锐角三角形、直角三角形、
钝角三角形?
3、直角三角形怎样表示?
4、直角三角形的两个锐角有什么关系?
A
B
C
我的课堂我做主-----我展示、我快乐
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是钝角
直角三角形
有一个内角是直角
直角三角形ABC用符号表示为
直角边是 _____和____ ,斜边是 。
直角三角形的两个锐角
Rt?ABC
BC
AC
AB
互余
1、
2、
3、
1、一个三角形两个内角的度数分别如下,
这个三角形是什么三角形?
(1)30°和60° ( )
(2)40°和70 ( )
(3)50°和30° ( )
直角三角形
锐角三角形
钝角三角形
比一比:
————我来小结:
(1)如图所示,以∠E为
内角的三角形有
(2)在△ACD中,
∠ACD的对边是 AC的对角
△ACE、△ABE
△ADE
1、
AD
∠ ADC
2、如图,已知∠ACB=90°,CD⊥AB,垂足是D
(1)图中有几个直角三角形?_______
是哪几个?(用符号表示出来)
__________________
(2)∠1和∠A有什么关系?∠2与∠A呢?
3个
Rt?ADC、 Rt?BDC、Rt?ACB
解:∠1+∠A=90°
∠2=∠A
理由:
∵ ∠1+∠A=90°
∠1+∠2=90°
∴ ∠2=∠A
解:
∵ ∠B+∠C+∠BAC=180°
∠B=40°,∠C=59°,
∴ ∠BAC=81°
∵ ∠BAC+∠EAF=180°
∴ ∠EAF=99°
∵ ∠ AEF=∠DEC=47°
∠F+ ∠EAF+∠ AEF=180°
∴ ∠F=34°
34°
用若干三角形组成一个美丽的图案,对图案加以形象的解说
爱心献给您
乘风破浪
再
见
祝同学们生活愉快!
学习进步!
解:如图,根据翻折的性质,
∠ADE=1/2(180-∠1)∠AED=1/2(180-∠2)
∵∠A+∠ADE+∠AED=180°
∴∠A+1/2(180-∠1)+1/2(180-∠2)=180°
∴2∠A=∠1+∠2
2、观察房屋屋顶的框架你能从中看出4个不同的三角形?
在小学我们探究了三角形三个内角的和等于180? ,你还记得这个结论的探索过程吗?
3.如图,已知∠B=40°,∠C=59°,
∠DEC=47°,则∠F=——
课外能力延伸:如图,将一张三角形纸片ABC沿DE折叠,使点A落到A′处,试说明∠A、∠1、∠2之间的数量关系
2、观察房屋屋顶的框架你能从中看出4个不同的三角形?
在小学我们探究了三角形三个内角的和等于180? ,你还记得这个结论的探索过程吗?
3.如图,已知∠B=40°,∠C=59°,
∠DEC=47°,则∠F=——
课外能力延伸:如图,将一张三角形纸片ABC沿DE折叠,使点A落到A′处,试说明∠A、∠1、∠2之间的数量关系
七 年 级 数 学
下册第四章
用若干三角形组成一个美丽的图案,对图案加以形象的解说
爱心献给您
乘风破浪
在小学我们探究了三角形三个内角的和等于180? ,你还记得这个结论的探索过程吗?
3.如图,已知∠B=40°,∠C=59°,
∠DEC=47°,则∠F=——
课外能力延伸:如图,将一张三角形纸片ABC沿DE折叠,使点A落到A′处,试说明∠A、∠1、∠2之间的数量关系
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
七 年 级 数 学
下册第四章
在这些优美的画面中,这些物体的侧面都是什么几何图形?
说一说:在日常生活中,还有
哪些三角形形状的物体。
学习目标
1、理解三角形及有关的概念,能用符号
语言表示三角形.
2、探索并证明三角形内角和等于180°,
3、会按角将三角形进行分类,能发现直角 三角形中两个锐角的关系.
1、三角形的定义:
首
尾
尾
首
尾
首
思考
定义中有几个限制条件?
由不在同一直线上的三条线段首尾顺次相接所组成的图形
拼一拼
1、如图是用三根细棍组成的图形, 其中符合三角形概念的图形( )
D
A
C
B
D
练习
斜梁
斜梁
直 梁
自学指导一:
认真看课本P81第二自然段的做一做以前的
内容。2分钟
重点看:
1、三角形的表示方法及其各部分的名称。
2、写出角的对边及边的对角。
(一)三角形的三要素:
边:
如图三角形中三边 AB、BC、AC。
顶点A所对的边BC也可表示为a,
顶点B所对的边AC也可表示为b ,
顶点C所对的边AB也可表示为c
角:
三角形中有三个角:
顶点:
三角形中有三个顶点:
∠B 的对边是_____
AC
∠A的对边是_____
∠C的对边是_____
BC
AB
∠A,∠B,∠C
顶点A,顶点B,顶点C
A
B
C
c
b
a
AC的对角是_____ BC的对角是_____ AB的对角是_____
∠B
∠A
∠C
一、三角形的相关概念:
A
B
C
记法:
三角形符号“△”,
如:上图的三角形记作:△ABC (或△ BCA或△ CBA 等)
注意: 顶点字母没有限定次序。
(二)如何表示三角形?
例、(1)图中以BC为边的三角形共有______个; 它们分别______________________________.
(2)在△ABD中, ∠ABD是____边的对角,
(3)∠BEC是△_______的内角
D
B
E
C
F
A
4
△BCF; △BCE; △BCD; △BCA
AD
BEC
三角形的三个内角有什么关系?
1
A
B
D
2
C
如图,当时我们是撕下两个角,把∠A移到了∠1的位置,把∠B移到了∠2的位置,三个角合在一起构成了一个平角.
如果只撕下三角形的一个角,你也能得到上面的结论吗?
讨论:如果只撕下三角形的一个角,能
不能得到三角形内角和等于180°?
认真看课本P81做一做
时间4分钟
利用准备好的三角形撕下一个角摆一摆,怎样摆那个撕下的角?才能得到三角形的内角和等于180°
摆出撕下的∠1,让∠1与∠2的顶点重合, ∠1一条边与∠2一边重合.
⌒
1
2
⌒
⌒
3
a
b
⌒
4
思考: ∠1的另一条边b与∠3边a是平行的吗?为什么?
你能得到∠1+ ∠2+∠3=180°请写出来
A
B
C
E
通过刚才的活动,给我们的启示:也可以直接过三角形的一 个顶点作平行线,也能证明三角形的内角和等于180°
已知:△A B C.
求证:∠A +∠B +∠C =180°
A
B
C
E
证明:延长BC到D过C作C E∥B A.
∵CE ∥B A
∴∠A= ∠ACE, ∠B=∠ECD
∵∠BCA+∠ACE+∠ECD=180°
∴ ∠BCA+∠A+∠B= 180°
------------
D
1、在△ABC中,
∠B=100?,∠A=∠C,则∠C=_______度;
40
2、 如图,已知∠B=10,∠C= 20°
∠BOC=110°求∠A的度数
解:延长OC至AB相交得点D
∵ ∠BOC+∠BOD= 180° ∠BOC=110°
∴∠BOD=70 °
∵ ∠BOD+∠BDO+∠B=180°∠B=10 °
∴∠BDO=100 °
∴∠ODA=80°
∵∠C+∠A+∠ODA=180 °
∴∠A=80 °
D
猜一猜
(1)下图中小明所拿三角形被遮住的两个内角是什么角?小颖的
呢?试着说明理由.
(2)下图中三角形被遮住的两个内角可能是什么角?将所
得结果与(1)的结果进行比较.
认真看课本P84练习以前的内容,时间3分钟。思考下列问题
1、三角形按角怎么分?
2、什么叫锐角三角形、直角三角形、
钝角三角形?
3、直角三角形怎样表示?
4、直角三角形的两个锐角有什么关系?
A
B
C
我的课堂我做主-----我展示、我快乐
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是钝角
直角三角形
有一个内角是直角
直角三角形ABC用符号表示为
直角边是 _____和____ ,斜边是 。
直角三角形的两个锐角
Rt?ABC
BC
AC
AB
互余
1、
2、
3、
1、一个三角形两个内角的度数分别如下,
这个三角形是什么三角形?
(1)30°和60° ( )
(2)40°和70 ( )
(3)50°和30° ( )
直角三角形
锐角三角形
钝角三角形
比一比:
————我来小结:
(1)如图所示,以∠E为
内角的三角形有
(2)在△ACD中,
∠ACD的对边是 AC的对角
△ACE、△ABE
△ADE
1、
AD
∠ ADC
2、如图,已知∠ACB=90°,CD⊥AB,垂足是D
(1)图中有几个直角三角形?_______
是哪几个?(用符号表示出来)
__________________
(2)∠1和∠A有什么关系?∠2与∠A呢?
3个
Rt?ADC、 Rt?BDC、Rt?ACB
解:∠1+∠A=90°
∠2=∠A
理由:
∵ ∠1+∠A=90°
∠1+∠2=90°
∴ ∠2=∠A
解:
∵ ∠B+∠C+∠BAC=180°
∠B=40°,∠C=59°,
∴ ∠BAC=81°
∵ ∠BAC+∠EAF=180°
∴ ∠EAF=99°
∵ ∠ AEF=∠DEC=47°
∠F+ ∠EAF+∠ AEF=180°
∴ ∠F=34°
34°
用若干三角形组成一个美丽的图案,对图案加以形象的解说
爱心献给您
乘风破浪
再
见
祝同学们生活愉快!
学习进步!
解:如图,根据翻折的性质,
∠ADE=1/2(180-∠1)∠AED=1/2(180-∠2)
∵∠A+∠ADE+∠AED=180°
∴∠A+1/2(180-∠1)+1/2(180-∠2)=180°
∴2∠A=∠1+∠2
2、观察房屋屋顶的框架你能从中看出4个不同的三角形?
在小学我们探究了三角形三个内角的和等于180? ,你还记得这个结论的探索过程吗?
3.如图,已知∠B=40°,∠C=59°,
∠DEC=47°,则∠F=——
课外能力延伸:如图,将一张三角形纸片ABC沿DE折叠,使点A落到A′处,试说明∠A、∠1、∠2之间的数量关系
2、观察房屋屋顶的框架你能从中看出4个不同的三角形?
在小学我们探究了三角形三个内角的和等于180? ,你还记得这个结论的探索过程吗?
3.如图,已知∠B=40°,∠C=59°,
∠DEC=47°,则∠F=——
课外能力延伸:如图,将一张三角形纸片ABC沿DE折叠,使点A落到A′处,试说明∠A、∠1、∠2之间的数量关系
七 年 级 数 学
下册第四章
用若干三角形组成一个美丽的图案,对图案加以形象的解说
爱心献给您
乘风破浪
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
