北师大版七年级下册数学:2.3 第一课时 平行线的性质综合应用 (共18张PPT)
文档属性
| 名称 | 北师大版七年级下册数学:2.3 第一课时 平行线的性质综合应用 (共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 120.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 13:21:28 | ||
图片预览




文档简介
第二章 相交线与平行线
3 平行线的性质(第1课时)
北师大版七年级下册第二章
(1) ∠1=∠5 (已知)
a∥b( )
(2) ∠4=∠ (已知)
a∥b(内错角相等,两直线平行 )
(3) ∠4+∠ =180° (已知)
a∥b( )
同位角相等,两直线平行
5
6
同旁内角互补,两直线平行
第一环节:复习回顾,逆向猜想
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
平行线的判定
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
?
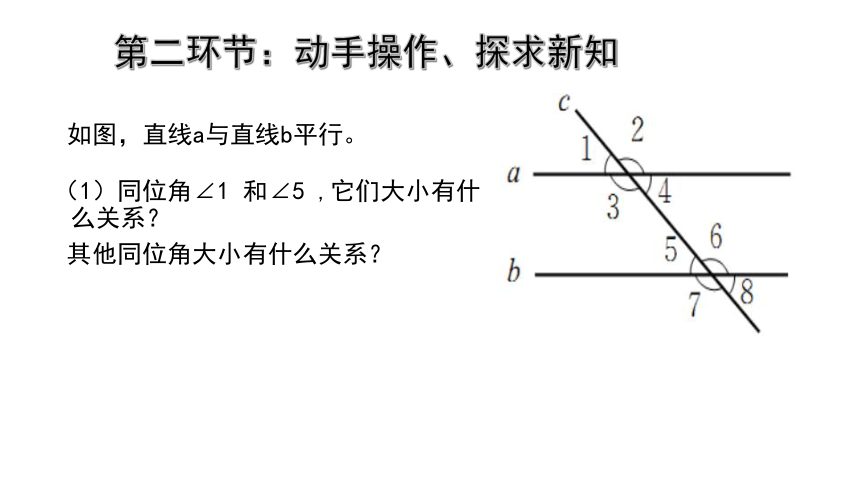
第二环节:动手操作、探求新知
如图,直线a与直线b平行。
(1)同位角∠1 和∠5 ,它们大小有什么关系?
其他同位角大小有什么关系?
∠1=∠5
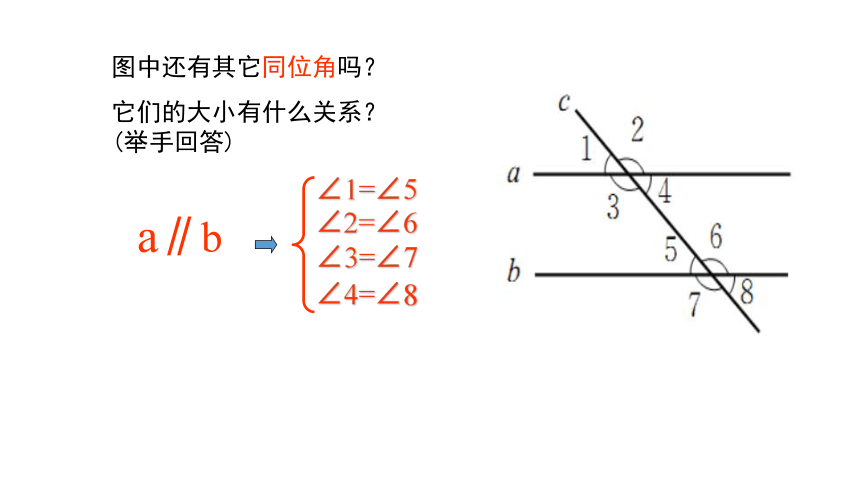
图中还有其它同位角吗?
它们的大小有什么关系?(举手回答)
∠2=∠6
∠3=∠7
∠4=∠8
a∥b
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
总结归纳
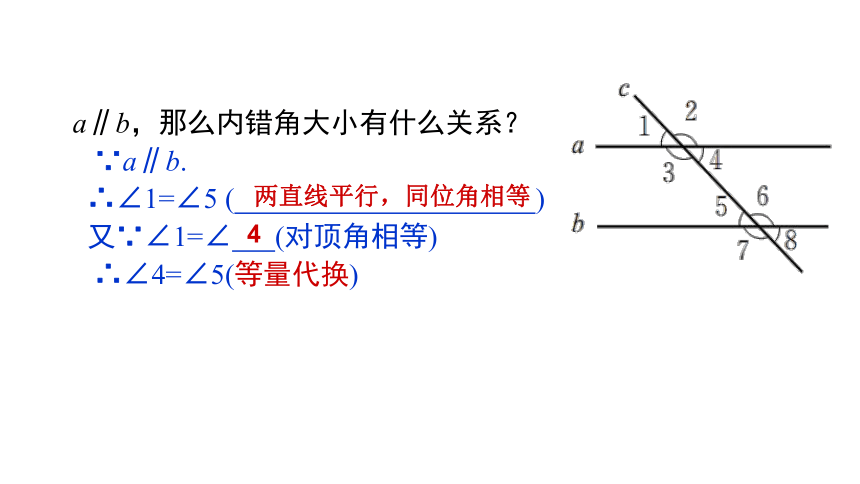
a∥b,那么内错角大小有什么关系?
∵a∥b.
∴∠1=∠5 ( )
又∵∠1=∠ (对顶角相等)
∴∠4=∠5(等量代换)
??
两直线平行,同位角相等
4
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
总结归纳
如果a∥b,
那么∠3+∠5=180°吗?
∵ a ∥ b (已知)
∴∠1=∠5( )
又∵ ∠1+∠3=180° ( )
∴ ∠3+∠5=180°
两直线平行,同位角相等
邻补角的定义
(等量代换)
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
总结归纳
两直线平行,同旁内角互补。
两直线平行,内错角相等。
两直线平行,同位角相等。
平行线的性质:
如图,与∠1相等的角有:
∠3, ∠5, ∠7, ∠9,
∠11, ∠13, ∠15;
与∠1互补的角有:
∠2, ∠4, ∠6, ∠8,
∠10, ∠12, ∠14, ∠16 ;
解:
1
14
16
13
15
3
A
B
D
C
2
4
5
6
7
8
9
10
12
11
第三环节:巩固新知,灵活运用
1、如图所示,AB∥CD,AC∥BD,
分别找出与∠1相等或互补的角。
请大家填写下面的表格,加以对比:
?
条件
结论
判定直线
平行
平行线
的性质
同位角相等
两直线平行
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
第四环节:对比学习,加深理解
同位角相等
两直线平行 内错角相等
同旁内角互补
判定
性质
判定:角的关系 线的关系????????????
性质:线的关系 角的关系
(同位角相等,两直线平行)
1、已知 ∠ADE=60 °,∠B=60 °,∠AED=40°
求证:(1)DE∥BC
(2)∠C的度数
E
D
C
B
A
(2)∵ DE∥BC
(已证)
∴ ∠AED=∠C
(两直线平行,同位角相等)
∵∠AED=40°
(等量代换)
∴∠C=40 °
证明(1)∵∠ADE=∠B=60 °
∴DE∥BC
第五个环节:联系拓广,综合应用
2. 如图:一束平行光线AB和DE射向一个水平镜面后被反射,
(1 )∠1,∠3的大小有什么关系?
∠2与∠4呢?
∵AB∥DE
∴∠1=∠3
相等:∠1=∠3;
(2 )反射光线BC与EF也平行吗?
∵ ∠2=∠4 ∴ BC∥EF
平行:
又∵ ∠1=∠2 ,∠3=∠4
∴ ∠2=∠4
A
B
D
E
C
F
此时∠1=∠2 , ∠3=∠4 。
1
3
2
4
∠2 =∠4 。
第六小节:课堂小结,布置作业。
1.本节课你有哪些收获?
2.作业:课本51页习题1.2.3
谢谢大家!
3 平行线的性质(第1课时)
北师大版七年级下册第二章
(1) ∠1=∠5 (已知)
a∥b( )
(2) ∠4=∠ (已知)
a∥b(内错角相等,两直线平行 )
(3) ∠4+∠ =180° (已知)
a∥b( )
同位角相等,两直线平行
5
6
同旁内角互补,两直线平行
第一环节:复习回顾,逆向猜想
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
平行线的判定
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
?
第二环节:动手操作、探求新知
如图,直线a与直线b平行。
(1)同位角∠1 和∠5 ,它们大小有什么关系?
其他同位角大小有什么关系?
∠1=∠5
图中还有其它同位角吗?
它们的大小有什么关系?(举手回答)
∠2=∠6
∠3=∠7
∠4=∠8
a∥b
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
总结归纳
a∥b,那么内错角大小有什么关系?
∵a∥b.
∴∠1=∠5 ( )
又∵∠1=∠ (对顶角相等)
∴∠4=∠5(等量代换)
??
两直线平行,同位角相等
4
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
总结归纳
如果a∥b,
那么∠3+∠5=180°吗?
∵ a ∥ b (已知)
∴∠1=∠5( )
又∵ ∠1+∠3=180° ( )
∴ ∠3+∠5=180°
两直线平行,同位角相等
邻补角的定义
(等量代换)
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
总结归纳
两直线平行,同旁内角互补。
两直线平行,内错角相等。
两直线平行,同位角相等。
平行线的性质:
如图,与∠1相等的角有:
∠3, ∠5, ∠7, ∠9,
∠11, ∠13, ∠15;
与∠1互补的角有:
∠2, ∠4, ∠6, ∠8,
∠10, ∠12, ∠14, ∠16 ;
解:
1
14
16
13
15
3
A
B
D
C
2
4
5
6
7
8
9
10
12
11
第三环节:巩固新知,灵活运用
1、如图所示,AB∥CD,AC∥BD,
分别找出与∠1相等或互补的角。
请大家填写下面的表格,加以对比:
?
条件
结论
判定直线
平行
平行线
的性质
同位角相等
两直线平行
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
第四环节:对比学习,加深理解
同位角相等
两直线平行 内错角相等
同旁内角互补
判定
性质
判定:角的关系 线的关系????????????
性质:线的关系 角的关系
(同位角相等,两直线平行)
1、已知 ∠ADE=60 °,∠B=60 °,∠AED=40°
求证:(1)DE∥BC
(2)∠C的度数
E
D
C
B
A
(2)∵ DE∥BC
(已证)
∴ ∠AED=∠C
(两直线平行,同位角相等)
∵∠AED=40°
(等量代换)
∴∠C=40 °
证明(1)∵∠ADE=∠B=60 °
∴DE∥BC
第五个环节:联系拓广,综合应用
2. 如图:一束平行光线AB和DE射向一个水平镜面后被反射,
(1 )∠1,∠3的大小有什么关系?
∠2与∠4呢?
∵AB∥DE
∴∠1=∠3
相等:∠1=∠3;
(2 )反射光线BC与EF也平行吗?
∵ ∠2=∠4 ∴ BC∥EF
平行:
又∵ ∠1=∠2 ,∠3=∠4
∴ ∠2=∠4
A
B
D
E
C
F
此时∠1=∠2 , ∠3=∠4 。
1
3
2
4
∠2 =∠4 。
第六小节:课堂小结,布置作业。
1.本节课你有哪些收获?
2.作业:课本51页习题1.2.3
谢谢大家!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
