北师大版七年级下册数学:4.3 角边角”“角角边”判定 课件(共18张PPT)
文档属性
| 名称 | 北师大版七年级下册数学:4.3 角边角”“角角边”判定 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 00:00:00 | ||
图片预览



文档简介
第四章 三角形复习
三角形全等
三角形全等的条件:
SSS ASA AAS SAS
三边分别相等的两个三角形全等,简写为“边边边”或“SSS”
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”
两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”
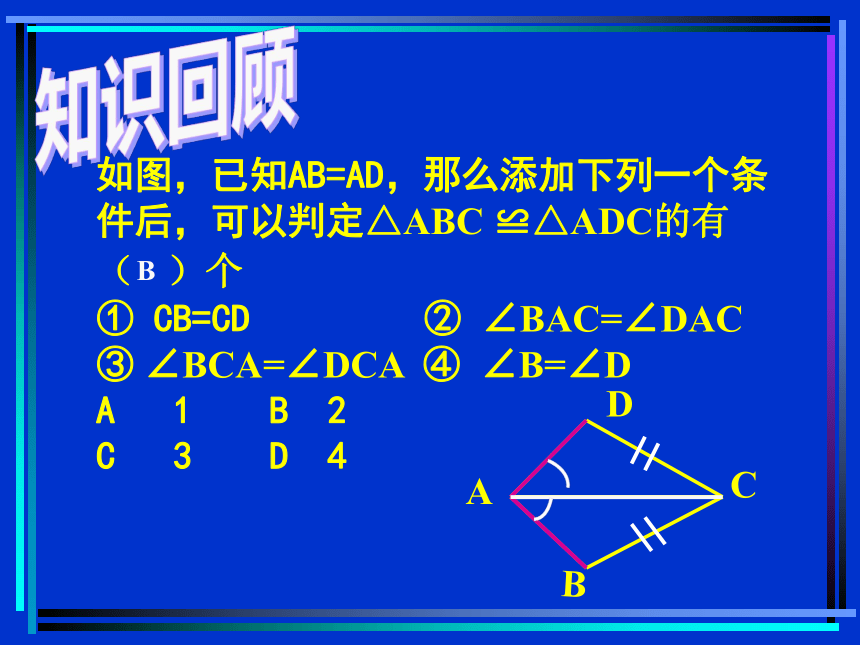
如图,已知AB=AD,那么添加下列一个条件后,可以判定△ABC ≌△ADC的有
( )个
① CB=CD ② ∠BAC=∠DAC
③ ∠BCA=∠DCA ④ ∠B=∠D
A 1 B 2
C 3 D 4
B
D
C
A
B
A
B
C
D
E
F
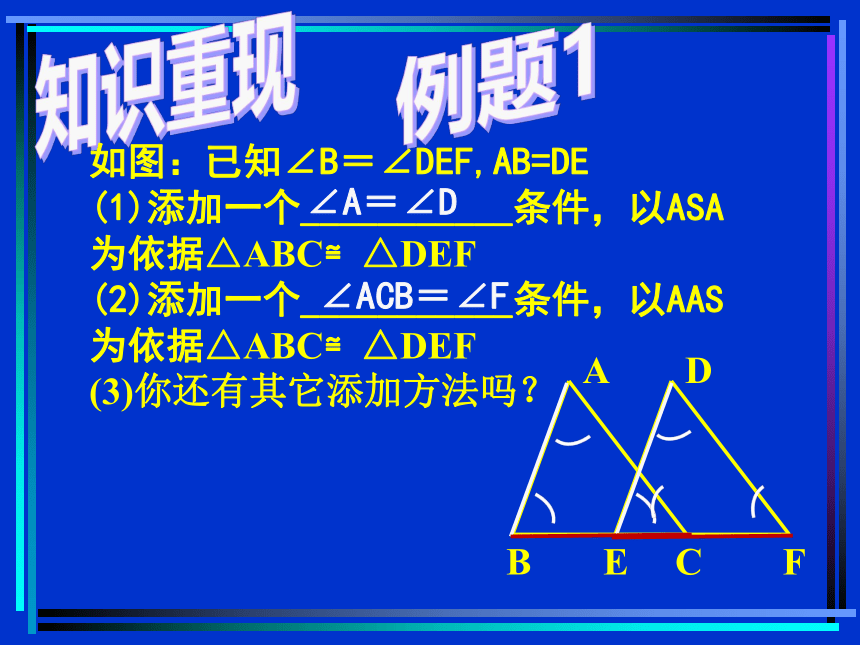
如图:已知∠B=∠DEF,AB=DE
(1)添加一个___________条件,以ASA为依据△ABC≌△DEF
(2)添加一个___________条件,以AAS为依据△ABC≌△DEF
(3)你还有其它添加方法吗?
∠A=∠D
∠ACB=∠F
F
A
B
C
D
E
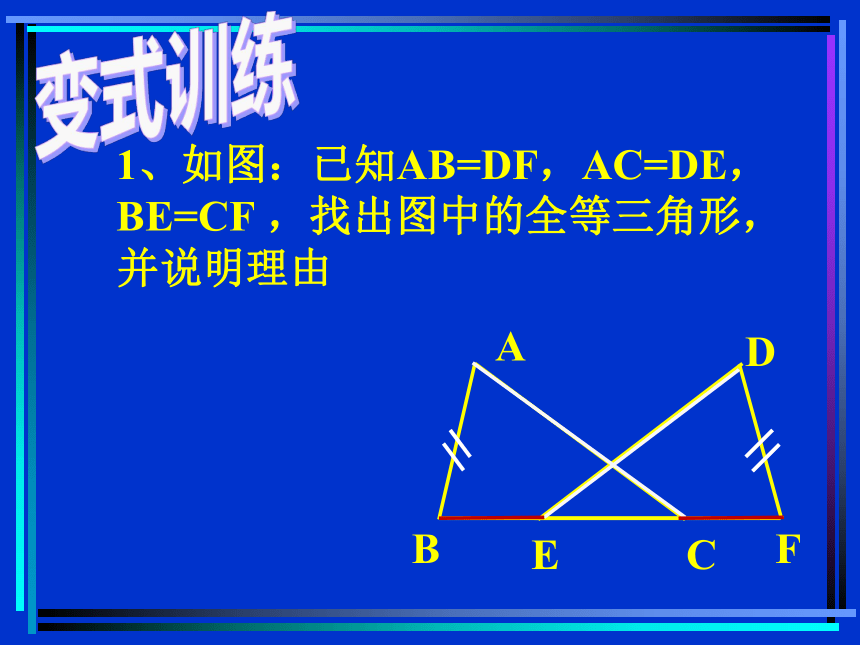
1、如图:已知AB=DF,AC=DE,BE=CF ,找出图中的全等三角形,并说明理由
F
A
B
C
D
E
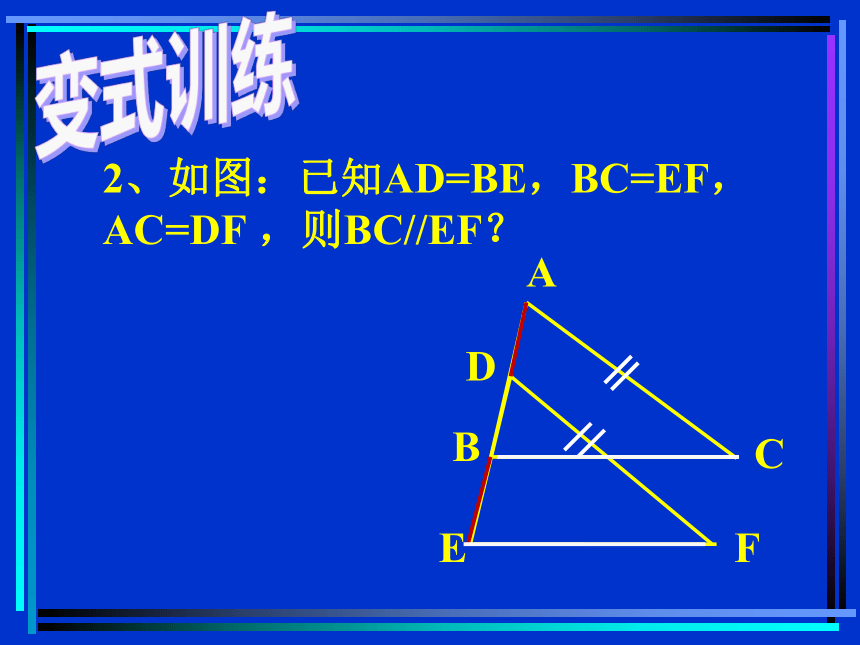
2、如图:已知AD=BE,BC=EF,AC=DF ,则BC//EF?
A
B
C
D
E
1
2
3﹑如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
如图,已知点E,F在BD上,AD//CB, AD=CB,∠A=∠C,
求证:DE=BF
A
B
D
C
E
F
A
B
D
C
E
F
1、如图:E、F是四边形ABCD的对角线BD上的两点,AE//CF,AE=CF,BE=DF
求证:AB//CD
A
B
D
C
E
F
2、如图:AD//BC,AD=BC,BF=DE,
问图中共有几对全等的三角形?请任选一对证明
C
B
D
E
A
F
本节课你学到了哪些知识?有哪些收获?
1、如图,AC与BD相交于点O,O是AC的中点,AB//CD,△AOB与△COD全等吗?为什么?
A
B
D
C
O
2、四边形ABCD对角线AC、BD交于点O,已知O是AC中点,AE=CF,DF//BE
求证: △BOE ≌△DOF
A
B
D
C
E
F
O
3、如图:E、F是四边形ABCD的对角线BD上的两点,AB=CD,AD=BC,且AE=CF,DE=BF
那么图中共有几对全等的三角形?
B
A
D
C
E
F
上交作业:课本P111 6(必做) 7(选做)
家庭作业:同步P91---94
三角形全等
三角形全等的条件:
SSS ASA AAS SAS
三边分别相等的两个三角形全等,简写为“边边边”或“SSS”
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”
两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”
如图,已知AB=AD,那么添加下列一个条件后,可以判定△ABC ≌△ADC的有
( )个
① CB=CD ② ∠BAC=∠DAC
③ ∠BCA=∠DCA ④ ∠B=∠D
A 1 B 2
C 3 D 4
B
D
C
A
B
A
B
C
D
E
F
如图:已知∠B=∠DEF,AB=DE
(1)添加一个___________条件,以ASA为依据△ABC≌△DEF
(2)添加一个___________条件,以AAS为依据△ABC≌△DEF
(3)你还有其它添加方法吗?
∠A=∠D
∠ACB=∠F
F
A
B
C
D
E
1、如图:已知AB=DF,AC=DE,BE=CF ,找出图中的全等三角形,并说明理由
F
A
B
C
D
E
2、如图:已知AD=BE,BC=EF,AC=DF ,则BC//EF?
A
B
C
D
E
1
2
3﹑如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
如图,已知点E,F在BD上,AD//CB, AD=CB,∠A=∠C,
求证:DE=BF
A
B
D
C
E
F
A
B
D
C
E
F
1、如图:E、F是四边形ABCD的对角线BD上的两点,AE//CF,AE=CF,BE=DF
求证:AB//CD
A
B
D
C
E
F
2、如图:AD//BC,AD=BC,BF=DE,
问图中共有几对全等的三角形?请任选一对证明
C
B
D
E
A
F
本节课你学到了哪些知识?有哪些收获?
1、如图,AC与BD相交于点O,O是AC的中点,AB//CD,△AOB与△COD全等吗?为什么?
A
B
D
C
O
2、四边形ABCD对角线AC、BD交于点O,已知O是AC中点,AE=CF,DF//BE
求证: △BOE ≌△DOF
A
B
D
C
E
F
O
3、如图:E、F是四边形ABCD的对角线BD上的两点,AB=CD,AD=BC,且AE=CF,DE=BF
那么图中共有几对全等的三角形?
B
A
D
C
E
F
上交作业:课本P111 6(必做) 7(选做)
家庭作业:同步P91---94
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
