北师大版七年级下册数学课件:2.3平行线的性质综合应用(共18张PPT)
文档属性
| 名称 | 北师大版七年级下册数学课件:2.3平行线的性质综合应用(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 122.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 15:15:31 | ||
图片预览






文档简介
2.3 平行线的性质综合应用
学习目标:
1、熟练应用平行线的性质和判定解决简单的问题;
2、初步学会简单的几何推理。
复习回顾:
平行线的性质
两条直线平行,同位角相等
两条直线平行,内错角相等
两条直线平行,同旁内角互补
平行线的判定
同位角相等,两条直线平行
内错角相等,两条直线平行
同旁内角互补,两条直线平行
二者之间的关系怎样?
互逆
活动1:推理与书写
如图,直线a,b被直线c所截,当∠1=∠2时,则a∥b。根据的是同位角相等,两直线平行。
(1)当∠2=∠3时,你能用推理的方式来说明a∥b吗?
∵∠2=∠3 ( )
已知
∠1=∠3 ( )
等量代换
∴∠1=∠2 ( )
∴a∥b ( )
同位角相等两直线平行
(2)若∠2+∠4=180°时,如何说明a∥b?
对顶角相等
c
b
a
2
4
1
3
活动2:平行线的判定的应用
(1)若 ∠1 = ∠2,可以判定哪两条直线平行?根据是什么?
(2)若∠2 = ∠M,可以判定哪两条直线平行?根据是什么?
(3)若 ∠2 +∠3 =180° ,可以判定哪两条直线平行?根据是 什么?
解:(1)∵∠1=∠2( )
∴BF//CD(_________________ )
(2)∵∠2=∠M( )
∴____//____(________________)
(3)∵∠2 +∠3 =180°
∴____//____ (___________________)
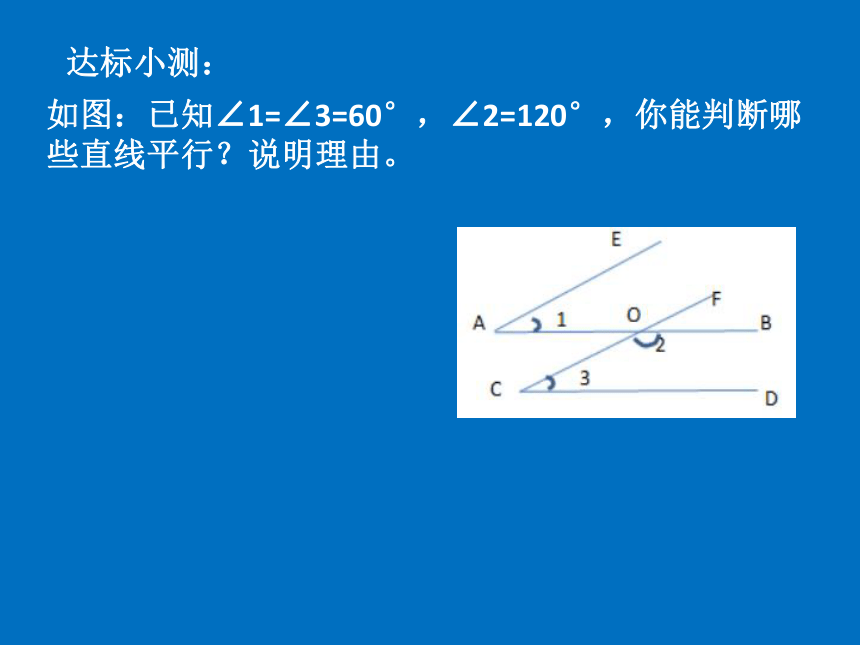
如图:已知∠1=∠3=60°,∠2=120°,你能判断哪些直线平行?说明理由。
达标小测:
例2:如图, AB∥CD,如果 ∠1 =∠2,那么 EF 与 AB 平行吗?说说你的理由
达标小测:
如图,AC平分∠BAD,∠1 =∠2,哪两条直线平行?说明理由。
例3:如图,已知直线 a∥b,直线 c∥d,∠1 = 107°,求 ∠2, ∠3 的度数.
活动3:平行的性质的应用
达标小测:
如图,已知AB∥DF,DE∥BC,∠1=65°,求∠2,∠3.
活动4:平行的判定和性质的综合应用
如图,平行直线AB,CD被直线EF所截,分别交直线AB,CD于点G,M。GH和MN分别是∠EGB和∠EMD的角平分线 ,问:GH和MN平行吗?请说明理由。
解:GH∥MN
∵AB∥CD
∴∠EGB=∠EMD( )
∵GH和MN分别是∠EGB和∠EMD的角平分线
∴∠EGH=?∠EGB ,∠EMN=?∠EMD
∴∠EGH=∠EMN
∴GH∥MN ( )
两直线平行,同位角相等
同位角相等,两直线平行
如图,已知,DE∥BC, ∠AED = 75° ,∠DFC = 105° ,
试说明DF∥AC.
达标小测:
F
E
D
C
B
A
合作探究、深化拓展:
已知AB∥CD,探索图形中∠D、∠E、∠B的关系,并加以说明.
若E点的位置如图所示,AB∥CD。那么∠D、∠E、∠B有怎样的关系,并加以说明
变式训练:
归纳小结、反思提高:
(1)、本节课你有哪些收获?
(2)、在应用平行的判定和性质时,应该注意哪些问题?
(3)、在书写几何推理的过程中,“因为”和“所以”分别表达的意义是什么?根据是什么?
1、如图,如果a∥b,∠1=60°,那么∠2=____,∠3=____、∠4=_____.
达标检测:
2、如图,
∴∠DBA=_____ ( _______________________ )
∵∠C=∠D (已知)
∴∠DBA=______(_____________________)
∴FD∥_____ (_____________________)
∴∠A=∠F (_________________________)
∠C
∠D
AC
两条直线平行,同位角相等
等量代换
内错角相等,两直线平行
两直线平行,内错角相等
∵BD∥EC(已知)
再 见
学习目标:
1、熟练应用平行线的性质和判定解决简单的问题;
2、初步学会简单的几何推理。
复习回顾:
平行线的性质
两条直线平行,同位角相等
两条直线平行,内错角相等
两条直线平行,同旁内角互补
平行线的判定
同位角相等,两条直线平行
内错角相等,两条直线平行
同旁内角互补,两条直线平行
二者之间的关系怎样?
互逆
活动1:推理与书写
如图,直线a,b被直线c所截,当∠1=∠2时,则a∥b。根据的是同位角相等,两直线平行。
(1)当∠2=∠3时,你能用推理的方式来说明a∥b吗?
∵∠2=∠3 ( )
已知
∠1=∠3 ( )
等量代换
∴∠1=∠2 ( )
∴a∥b ( )
同位角相等两直线平行
(2)若∠2+∠4=180°时,如何说明a∥b?
对顶角相等
c
b
a
2
4
1
3
活动2:平行线的判定的应用
(1)若 ∠1 = ∠2,可以判定哪两条直线平行?根据是什么?
(2)若∠2 = ∠M,可以判定哪两条直线平行?根据是什么?
(3)若 ∠2 +∠3 =180° ,可以判定哪两条直线平行?根据是 什么?
解:(1)∵∠1=∠2( )
∴BF//CD(_________________ )
(2)∵∠2=∠M( )
∴____//____(________________)
(3)∵∠2 +∠3 =180°
∴____//____ (___________________)
如图:已知∠1=∠3=60°,∠2=120°,你能判断哪些直线平行?说明理由。
达标小测:
例2:如图, AB∥CD,如果 ∠1 =∠2,那么 EF 与 AB 平行吗?说说你的理由
达标小测:
如图,AC平分∠BAD,∠1 =∠2,哪两条直线平行?说明理由。
例3:如图,已知直线 a∥b,直线 c∥d,∠1 = 107°,求 ∠2, ∠3 的度数.
活动3:平行的性质的应用
达标小测:
如图,已知AB∥DF,DE∥BC,∠1=65°,求∠2,∠3.
活动4:平行的判定和性质的综合应用
如图,平行直线AB,CD被直线EF所截,分别交直线AB,CD于点G,M。GH和MN分别是∠EGB和∠EMD的角平分线 ,问:GH和MN平行吗?请说明理由。
解:GH∥MN
∵AB∥CD
∴∠EGB=∠EMD( )
∵GH和MN分别是∠EGB和∠EMD的角平分线
∴∠EGH=?∠EGB ,∠EMN=?∠EMD
∴∠EGH=∠EMN
∴GH∥MN ( )
两直线平行,同位角相等
同位角相等,两直线平行
如图,已知,DE∥BC, ∠AED = 75° ,∠DFC = 105° ,
试说明DF∥AC.
达标小测:
F
E
D
C
B
A
合作探究、深化拓展:
已知AB∥CD,探索图形中∠D、∠E、∠B的关系,并加以说明.
若E点的位置如图所示,AB∥CD。那么∠D、∠E、∠B有怎样的关系,并加以说明
变式训练:
归纳小结、反思提高:
(1)、本节课你有哪些收获?
(2)、在应用平行的判定和性质时,应该注意哪些问题?
(3)、在书写几何推理的过程中,“因为”和“所以”分别表达的意义是什么?根据是什么?
1、如图,如果a∥b,∠1=60°,那么∠2=____,∠3=____、∠4=_____.
达标检测:
2、如图,
∴∠DBA=_____ ( _______________________ )
∵∠C=∠D (已知)
∴∠DBA=______(_____________________)
∴FD∥_____ (_____________________)
∴∠A=∠F (_________________________)
∠C
∠D
AC
两条直线平行,同位角相等
等量代换
内错角相等,两直线平行
两直线平行,内错角相等
∵BD∥EC(已知)
再 见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
