北师大版数学八年级下册3.1 图形的平移第1课时课件(共18张PPT)
文档属性
| 名称 | 北师大版数学八年级下册3.1 图形的平移第1课时课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 276.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 15:23:01 | ||
图片预览





文档简介
3.1 图形的平移
第1课时
第三章 图形的平移与旋转
一、 学习目标
1.通过具体实例认识平面图形的平移,探索它的基本性质。
2.会进行简单的平移画图。
(1)你能发现传送带上的行李箱、手扶电梯上的人在平移前后什么没有改变,什么发生了改变吗?
二、 情境导入
(2)在传送带上,如果行李箱的某一部位向前移动了80 cm,那么行李箱的其它部位向什么方向移动?移动了多少距离?
(3)如果把移动前后的行李箱分别记为四边形ABCD和四边形 ,那么两个四边形的形状、大小是否相同?
二、 情境导入
平移定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
平移不改变图形的形状和大小.
三、 探究新知
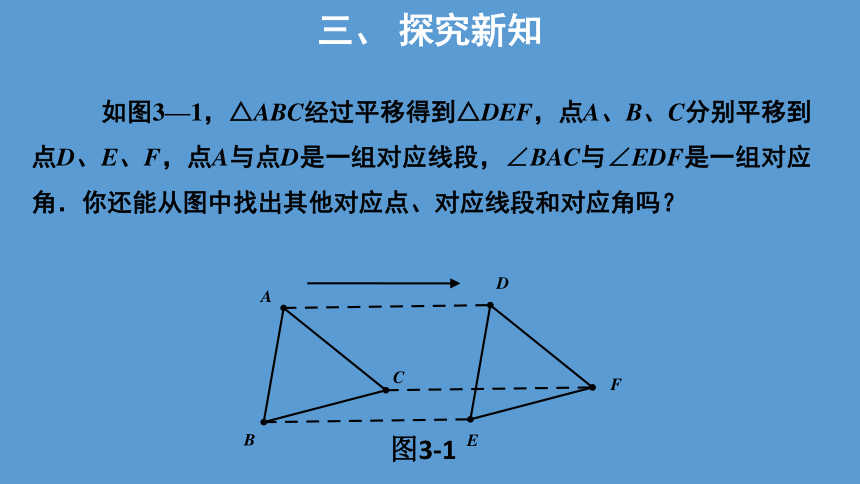
?如图3—1,△ABC经过平移得到△DEF,点A、B、C分别平移到点D、E、F,点A与点D是一组对应线段,∠BAC与∠EDF是一组对应角.你还能从图中找出其他对应点、对应线段和对应角吗?
图3-1
三、 探究新知
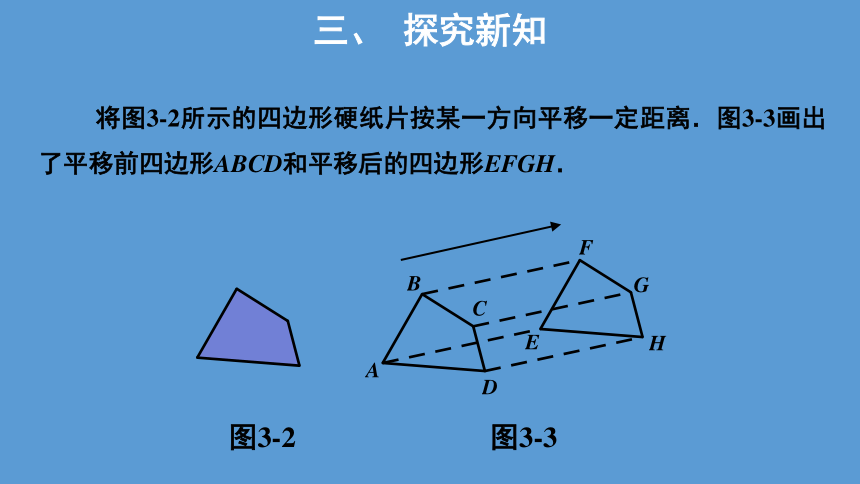
将图3-2所示的四边形硬纸片按某一方向平移一定距离.图3-3画出了平移前四边形ABCD和平移后的四边形EFGH.
图3-2
图3-3
三、 探究新知
(1)在图中任意选一组对应线段,这两条线段之间有怎样的关系?
(2)在图中任意选一组对应角,这两个角之间有怎样的关系?
(3)线段AE,BF,CG,DH分别是对应点所连成的线段,它们之间有怎样的关系?
三、 探究新知
讨论分析:
(1)变换前后对应线段平行且相等.
(2)变换前后对应角相等.
(3)变换前后对应点的连线平行且相等:平移变换是图形的每一个点的变换,一个图形沿某个方向移动一定距离,那么每一个点也沿着这个放向移动一定距离,所以对应点的连线平行且相等.
三、 探究新知
平移的性质:
经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
三、 探究新知
例1 如图,已知△ABC,D点是△ABC平移后A点的对应点.
(1)指出平移的方向和距离;
(2)请作出平移后的△DEF.
四、 典例精讲
(1)连接并延长AD(找到平移方向,平移距离).
四、 典例精讲
(2)过B,C两点分别作BE,CF平行于AD
(找到关键点,并作出它们的平移方向).
E
F
四、 典例精讲
(3)分别在BE,CF上截取BE=AD,CF=AD(截取平移距离,找到关键点的平移对应点).
E
F
四、 典例精讲
(4)连接D,E,F(连接关键点的对应点,构成平移图形).
(5)△DEF即为所求(写出结论).
E
F
四、 典例精讲
如图,点A,B,C,D,E,F都在网格纸的格点上,你能平移线段AB,使AB与CD重合吗?你能平移线段AB,使AB与EF重合吗?
把线段AB向右平移2格,再向上平移1格,则AB与CD重合;
不能平移线段AB使得AB与CD重合.
五、 课堂练习
1.平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.平移是由移动的方向和距离决定的.
2.平移的性质:
(1)平移不改变图形的形状和大小:即平移前后的线段相等,平移前后的三角形或多边形全等.
(2)平移后的图形与原来图形的对应线段平行且相等,对应角相等.
(3)平移后两图形的对应点所连的线段平行且相等.
六、 课堂小结
再见
第1课时
第三章 图形的平移与旋转
一、 学习目标
1.通过具体实例认识平面图形的平移,探索它的基本性质。
2.会进行简单的平移画图。
(1)你能发现传送带上的行李箱、手扶电梯上的人在平移前后什么没有改变,什么发生了改变吗?
二、 情境导入
(2)在传送带上,如果行李箱的某一部位向前移动了80 cm,那么行李箱的其它部位向什么方向移动?移动了多少距离?
(3)如果把移动前后的行李箱分别记为四边形ABCD和四边形 ,那么两个四边形的形状、大小是否相同?
二、 情境导入
平移定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
平移不改变图形的形状和大小.
三、 探究新知
?如图3—1,△ABC经过平移得到△DEF,点A、B、C分别平移到点D、E、F,点A与点D是一组对应线段,∠BAC与∠EDF是一组对应角.你还能从图中找出其他对应点、对应线段和对应角吗?
图3-1
三、 探究新知
将图3-2所示的四边形硬纸片按某一方向平移一定距离.图3-3画出了平移前四边形ABCD和平移后的四边形EFGH.
图3-2
图3-3
三、 探究新知
(1)在图中任意选一组对应线段,这两条线段之间有怎样的关系?
(2)在图中任意选一组对应角,这两个角之间有怎样的关系?
(3)线段AE,BF,CG,DH分别是对应点所连成的线段,它们之间有怎样的关系?
三、 探究新知
讨论分析:
(1)变换前后对应线段平行且相等.
(2)变换前后对应角相等.
(3)变换前后对应点的连线平行且相等:平移变换是图形的每一个点的变换,一个图形沿某个方向移动一定距离,那么每一个点也沿着这个放向移动一定距离,所以对应点的连线平行且相等.
三、 探究新知
平移的性质:
经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
三、 探究新知
例1 如图,已知△ABC,D点是△ABC平移后A点的对应点.
(1)指出平移的方向和距离;
(2)请作出平移后的△DEF.
四、 典例精讲
(1)连接并延长AD(找到平移方向,平移距离).
四、 典例精讲
(2)过B,C两点分别作BE,CF平行于AD
(找到关键点,并作出它们的平移方向).
E
F
四、 典例精讲
(3)分别在BE,CF上截取BE=AD,CF=AD(截取平移距离,找到关键点的平移对应点).
E
F
四、 典例精讲
(4)连接D,E,F(连接关键点的对应点,构成平移图形).
(5)△DEF即为所求(写出结论).
E
F
四、 典例精讲
如图,点A,B,C,D,E,F都在网格纸的格点上,你能平移线段AB,使AB与CD重合吗?你能平移线段AB,使AB与EF重合吗?
把线段AB向右平移2格,再向上平移1格,则AB与CD重合;
不能平移线段AB使得AB与CD重合.
五、 课堂练习
1.平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.平移是由移动的方向和距离决定的.
2.平移的性质:
(1)平移不改变图形的形状和大小:即平移前后的线段相等,平移前后的三角形或多边形全等.
(2)平移后的图形与原来图形的对应线段平行且相等,对应角相等.
(3)平移后两图形的对应点所连的线段平行且相等.
六、 课堂小结
再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
