北师大版数学八年级下册3.1 图形的平移第2课时课件(共16张PPT)
文档属性
| 名称 | 北师大版数学八年级下册3.1 图形的平移第2课时课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 214.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 15:22:14 | ||
图片预览




文档简介
3.1 图形的平移
第2课时
第三章 图形的平移与旋转
一、 学习目标
在直角坐标系中,能写出一个已知顶点坐标的多边形沿坐标轴方向平移
后图形的顶点坐标,并知道对应顶点坐标之间的关系。
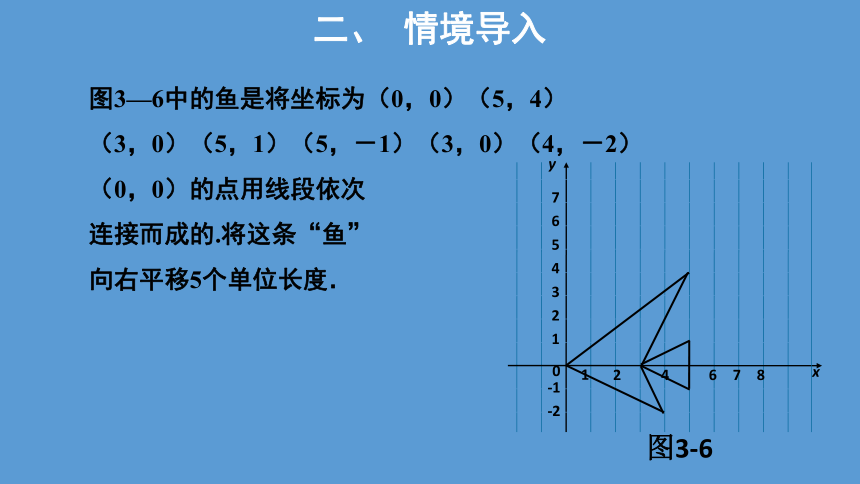
图3—6中的鱼是将坐标为(0,0)(5,4)
(3,0)(5,1)(5,-1)(3,0)(4,-2)
(0,0)的点用线段依次
连接而成的.将这条“鱼”
向右平移5个单位长度.
1
2
3
4
5
6
7
0
-1
-2
2
4
6
7
8
1
x
y
图3-6
二、 情境导入
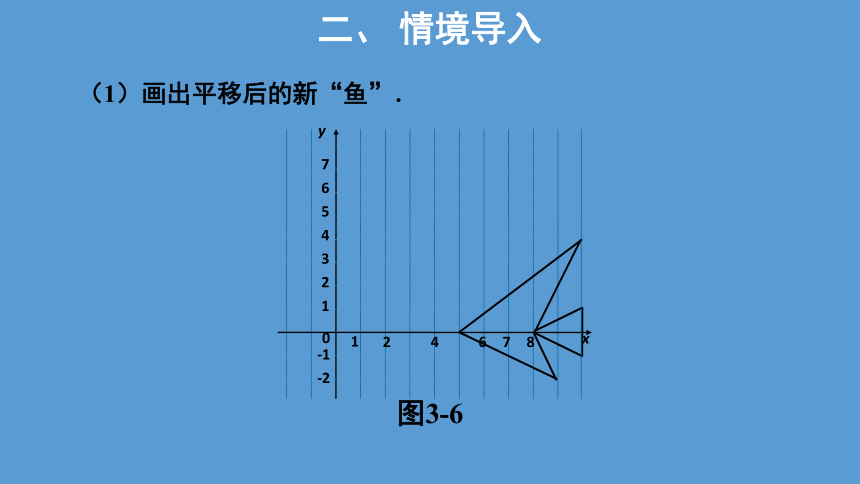
(1)画出平移后的新“鱼”.
1
2
3
4
5
6
7
0
-1
-2
2
4
6
7
8
1
x
y
图3-6
二、 情境导入
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
原来的“鱼”
向右平移5个
单位长度后
的新“鱼”
( , )
( , )
( , )
…….
( , )
( , )
( , )
…….
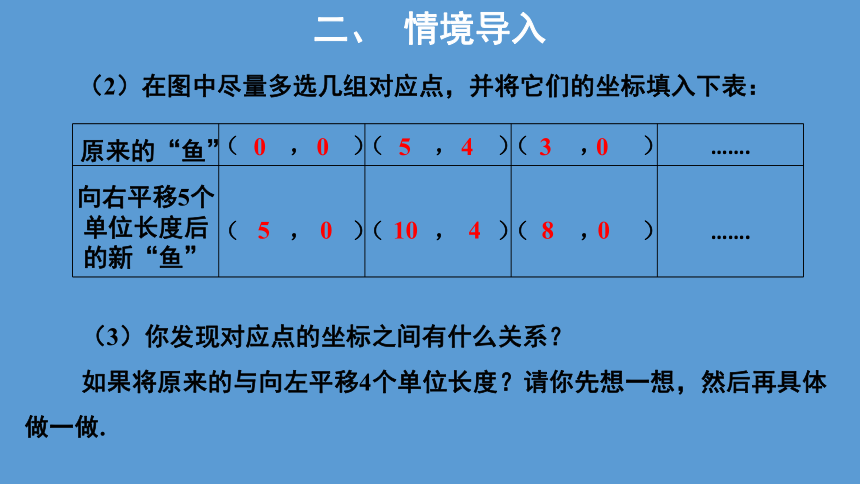
(3)你发现对应点的坐标之间有什么关系?
如果将原来的与向左平移4个单位长度?请你先想一想,然后再具体做一做.
(2)在图中尽量多选几组对应点,并将它们的坐标填入下表:
0 0
5 4
3 0
5 0
10 4
8 0
二、 情境导入
如果将图3—6中的“鱼”向上平移3个单位长度,那么平移前后的两条鱼中,对应的坐标之间有什么关系?
平移前后相对比,对应点的横坐标不变,纵坐标分别增加了3.
平移前后相对比,对应点的横坐标不变,纵坐标分别减小了2.
如果将图3—6中的“鱼”向下平移2个单位长度呢?
三、探究新知
(1)将图3—6中的“鱼”的每个“顶点”的纵坐标保持不变,横坐标分别加3,再将得到的点用线段依次连接起来,从而画出一条新“鱼”,这条新“鱼”与原来的“鱼”相比有什么变化?如果纵坐标保持不变,横坐标分别减2呢?
新“鱼”与原来的“鱼”相比,形状和大小都没发生改变,只是沿x轴向右平移了3个单位长度.若纵坐标保持不变,横坐标分别减2,则形状和大小都没改变,只是沿x轴向左平移了2个单位长度.
三、 探究新知
(2)将图3—6中的“鱼”的每个“顶点”的横坐标保持不变,纵坐标分别加3,所得到的新“鱼”与原来的“鱼”相比有什么变化?如果横坐标保持不变,纵坐标分别减2呢?
新“鱼”与原来的“鱼”相比,形状和大小都没发生改变,只是沿y轴向上平移了3个单位长度.若横坐标保持不变,纵坐标分别减2,则形状和大小都没改变,只是沿y轴向下平移了2个单位长度.
三、 探究新知
一般地,在平面直角坐标系中,
将点(x,y)向右(或左)平移a个单位长度,可以得到对应点的坐标是(x+a,y)或(x-a,y);
将点(x,y)向上(或下)平移b个单位长度,可以得到对应点的坐标是(x,y+b)或(x,y-b).
三、 探究新知
1.四边形ABCD的顶点坐标分别是A(0,3),B(﹣3,0),C(0,﹣3),D(3,0).
(1)将四边形ABCD向右平移6个单位长度,得到四边形 ,写出四边形 各顶点的坐标;
答:
(2)将四边形 向上平移6个单位长度,得到四边形 ,写出四边形 各顶点的坐标.
答:
四、 课堂练习
2.(1)将第1题中的四边形 各顶点的纵坐标不变,横坐标分别减4,得到四边形 它与四边形 相比有什么变化?
答:四边形 是由四边形 向左平移4个单位长度得到的 .
四、 课堂练习
(2)将四边形 各顶点的横坐标不变,纵坐标分别减4,得到四边形 ,它与四边形 相比有什么变化?
答:四边形 是由四边形 向下平移4个单位长度得到的 .
四、 课堂练习
归纳总结如下:
一般地,在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点的坐标是(x+a,y)或(x-a,y);
将点(x,y)向上(或下)平移b个单位长度,可以得到对应点的坐标是(x,y+b)或(x,y-b).
五、 课堂小结
再见
第2课时
第三章 图形的平移与旋转
一、 学习目标
在直角坐标系中,能写出一个已知顶点坐标的多边形沿坐标轴方向平移
后图形的顶点坐标,并知道对应顶点坐标之间的关系。
图3—6中的鱼是将坐标为(0,0)(5,4)
(3,0)(5,1)(5,-1)(3,0)(4,-2)
(0,0)的点用线段依次
连接而成的.将这条“鱼”
向右平移5个单位长度.
1
2
3
4
5
6
7
0
-1
-2
2
4
6
7
8
1
x
y
图3-6
二、 情境导入
(1)画出平移后的新“鱼”.
1
2
3
4
5
6
7
0
-1
-2
2
4
6
7
8
1
x
y
图3-6
二、 情境导入
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
原来的“鱼”
向右平移5个
单位长度后
的新“鱼”
( , )
( , )
( , )
…….
( , )
( , )
( , )
…….
(3)你发现对应点的坐标之间有什么关系?
如果将原来的与向左平移4个单位长度?请你先想一想,然后再具体做一做.
(2)在图中尽量多选几组对应点,并将它们的坐标填入下表:
0 0
5 4
3 0
5 0
10 4
8 0
二、 情境导入
如果将图3—6中的“鱼”向上平移3个单位长度,那么平移前后的两条鱼中,对应的坐标之间有什么关系?
平移前后相对比,对应点的横坐标不变,纵坐标分别增加了3.
平移前后相对比,对应点的横坐标不变,纵坐标分别减小了2.
如果将图3—6中的“鱼”向下平移2个单位长度呢?
三、探究新知
(1)将图3—6中的“鱼”的每个“顶点”的纵坐标保持不变,横坐标分别加3,再将得到的点用线段依次连接起来,从而画出一条新“鱼”,这条新“鱼”与原来的“鱼”相比有什么变化?如果纵坐标保持不变,横坐标分别减2呢?
新“鱼”与原来的“鱼”相比,形状和大小都没发生改变,只是沿x轴向右平移了3个单位长度.若纵坐标保持不变,横坐标分别减2,则形状和大小都没改变,只是沿x轴向左平移了2个单位长度.
三、 探究新知
(2)将图3—6中的“鱼”的每个“顶点”的横坐标保持不变,纵坐标分别加3,所得到的新“鱼”与原来的“鱼”相比有什么变化?如果横坐标保持不变,纵坐标分别减2呢?
新“鱼”与原来的“鱼”相比,形状和大小都没发生改变,只是沿y轴向上平移了3个单位长度.若横坐标保持不变,纵坐标分别减2,则形状和大小都没改变,只是沿y轴向下平移了2个单位长度.
三、 探究新知
一般地,在平面直角坐标系中,
将点(x,y)向右(或左)平移a个单位长度,可以得到对应点的坐标是(x+a,y)或(x-a,y);
将点(x,y)向上(或下)平移b个单位长度,可以得到对应点的坐标是(x,y+b)或(x,y-b).
三、 探究新知
1.四边形ABCD的顶点坐标分别是A(0,3),B(﹣3,0),C(0,﹣3),D(3,0).
(1)将四边形ABCD向右平移6个单位长度,得到四边形 ,写出四边形 各顶点的坐标;
答:
(2)将四边形 向上平移6个单位长度,得到四边形 ,写出四边形 各顶点的坐标.
答:
四、 课堂练习
2.(1)将第1题中的四边形 各顶点的纵坐标不变,横坐标分别减4,得到四边形 它与四边形 相比有什么变化?
答:四边形 是由四边形 向左平移4个单位长度得到的 .
四、 课堂练习
(2)将四边形 各顶点的横坐标不变,纵坐标分别减4,得到四边形 ,它与四边形 相比有什么变化?
答:四边形 是由四边形 向下平移4个单位长度得到的 .
四、 课堂练习
归纳总结如下:
一般地,在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点的坐标是(x+a,y)或(x-a,y);
将点(x,y)向上(或下)平移b个单位长度,可以得到对应点的坐标是(x,y+b)或(x,y-b).
五、 课堂小结
再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
