北师大版数学八年级下册6.3 三角形的中位线课件(共19张PPT)
文档属性
| 名称 | 北师大版数学八年级下册6.3 三角形的中位线课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 682.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 15:29:25 | ||
图片预览



文档简介
6.3 三角形的中位线
第六章 平行四边形
一、 学习目标
1.经历探索三角形中位线定理的过程,发展合情推理能力。
2. 证明三角形中位线定理,发展演绎推理能力。
3.运用三角形中位线定理解决简单问题。
F
E
D
C
B
A
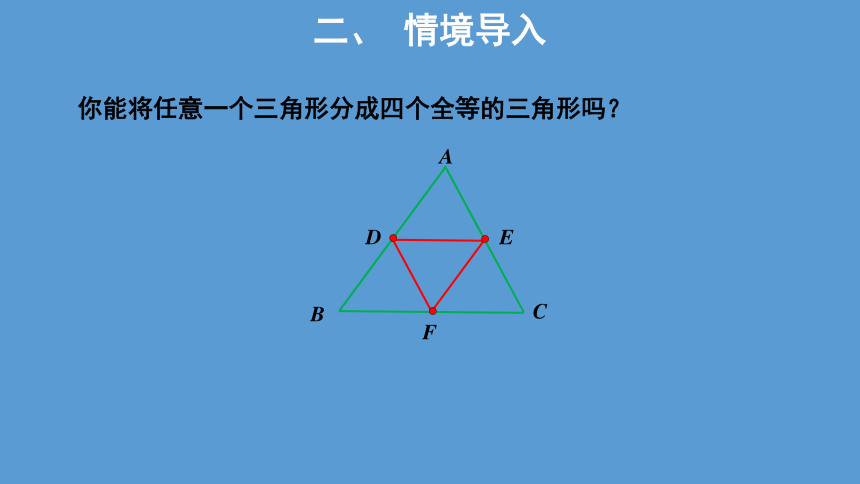
你能将任意一个三角形分成四个全等的三角形吗?
二、 情境导入
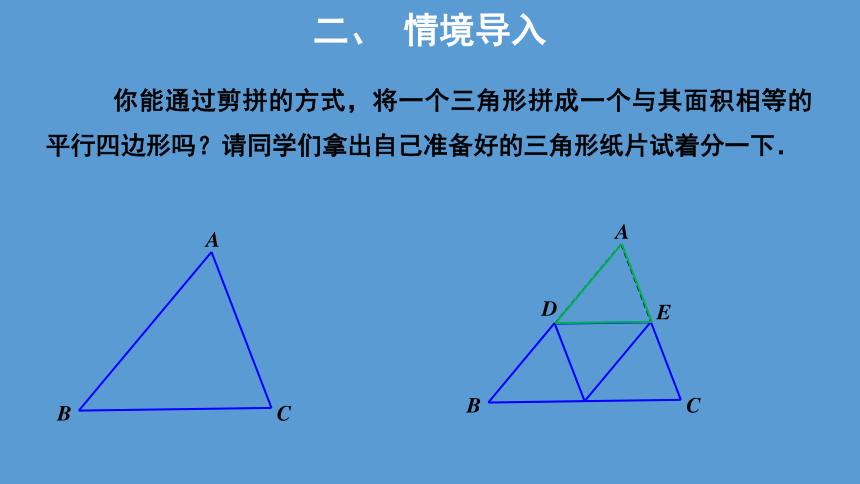
你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?请同学们拿出自己准备好的三角形纸片试着分一下.
C
B
A
E
D
C
B
A
二、 情境导入
F
E
D
C
B
A
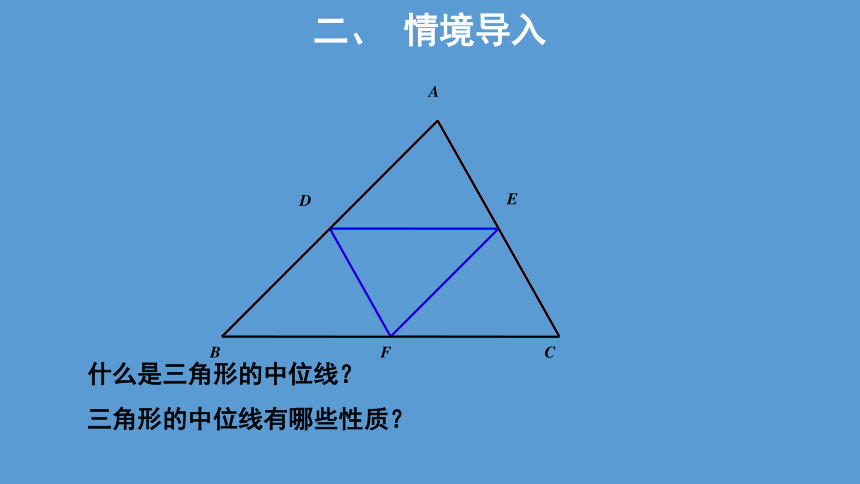
什么是三角形的中位线?
三角形的中位线有哪些性质?
二、 情境导入
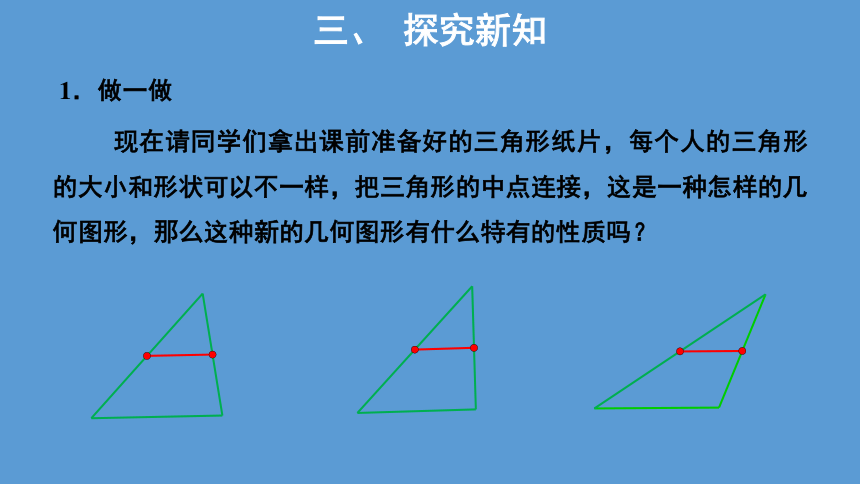
1.做一做
现在请同学们拿出课前准备好的三角形纸片,每个人的三角形的大小和形状可以不一样,把三角形的中点连接,这是一种怎样的几何图形,那么这种新的几何图形有什么特有的性质吗?
三、 探究新知
2.议一议 明晰结论
A
B
C
D
E
猜想:DE∥BC,DE= BC.
三、 探究新知
结论用文字表述:
三角形的中位线:
连接三角形两边中点的线段叫做三角形的中位线.
三角形中位线定理:
三角形的中位线平行于第三边,且等于第三边的一半.
三、 探究新知
已知:如图,DE是△ABC的中位线.
求证:DE∥BC,DE= BC.
E
D
C
B
A
三、 探究新知
证明:如图,延长DE到F ,使FE=DE,连接CF .
∵在△ADE和△ CFE中,AE=CE,∠AED=∠CEF,FE=DE,
∴△ADE≌CFE.
F
E
D
C
B
A
三、 探究新知
∴∠A=∠ECF,AD=CF.
∴CF∥AB.
∵BD=AD,
∴CF=BD.
∴四边形DBCF是平行四边形(一组对边平行且相等的四边形是平行四边形).
F
E
D
C
B
A
三、 探究新知
∴DF∥BC(平行四边形定义),
DF=BC(平行四边形对边相等).
∴DE∥BC,DE= BC.
F
E
D
C
B
A
三、 探究新知
例1 已知三角形的各边长分别为8cm,10cm,12cm,求以各边中点为顶点的三角形的周长.
F
A
B
C
D
E
四、 典例精讲
解: 如图,设三角形及其中点如图所示,
则由三角形中位线定理可得:
DE= BC,DF= AC,EF= AB,
∵AB +BC +AC=8cm+10cm+12cm=20cm.
∴DE +DF +EF=10cm(三角形中位线等于底边一半).
∴各边中点为顶点的三角形的周长为10cm.
F
A
B
C
D
E
四、 典例精讲
1.已知直角三角形的两条直角边长分别为6和8,则连接
这两条直角边中点的线段长为 ( ).
A.3 B.4 C.5 D.6
C
五、 课堂练习
2.如图,D,E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD的度数是( ).
A.42° B.48° C.52° D.58°
B
五、 课堂练习
1.通过动手活动对获得的定理给予了直观的感受,为今后解决有关三角形中位线的问题提供了丰富的理论依据.
(1)三角形中位线平行于底边.
(2)三角形中位线等于底边的一半.
2.体会了证明命题的严格的要求,体会了证明的必要性.
六、 课堂小结
再见
第六章 平行四边形
一、 学习目标
1.经历探索三角形中位线定理的过程,发展合情推理能力。
2. 证明三角形中位线定理,发展演绎推理能力。
3.运用三角形中位线定理解决简单问题。
F
E
D
C
B
A
你能将任意一个三角形分成四个全等的三角形吗?
二、 情境导入
你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?请同学们拿出自己准备好的三角形纸片试着分一下.
C
B
A
E
D
C
B
A
二、 情境导入
F
E
D
C
B
A
什么是三角形的中位线?
三角形的中位线有哪些性质?
二、 情境导入
1.做一做
现在请同学们拿出课前准备好的三角形纸片,每个人的三角形的大小和形状可以不一样,把三角形的中点连接,这是一种怎样的几何图形,那么这种新的几何图形有什么特有的性质吗?
三、 探究新知
2.议一议 明晰结论
A
B
C
D
E
猜想:DE∥BC,DE= BC.
三、 探究新知
结论用文字表述:
三角形的中位线:
连接三角形两边中点的线段叫做三角形的中位线.
三角形中位线定理:
三角形的中位线平行于第三边,且等于第三边的一半.
三、 探究新知
已知:如图,DE是△ABC的中位线.
求证:DE∥BC,DE= BC.
E
D
C
B
A
三、 探究新知
证明:如图,延长DE到F ,使FE=DE,连接CF .
∵在△ADE和△ CFE中,AE=CE,∠AED=∠CEF,FE=DE,
∴△ADE≌CFE.
F
E
D
C
B
A
三、 探究新知
∴∠A=∠ECF,AD=CF.
∴CF∥AB.
∵BD=AD,
∴CF=BD.
∴四边形DBCF是平行四边形(一组对边平行且相等的四边形是平行四边形).
F
E
D
C
B
A
三、 探究新知
∴DF∥BC(平行四边形定义),
DF=BC(平行四边形对边相等).
∴DE∥BC,DE= BC.
F
E
D
C
B
A
三、 探究新知
例1 已知三角形的各边长分别为8cm,10cm,12cm,求以各边中点为顶点的三角形的周长.
F
A
B
C
D
E
四、 典例精讲
解: 如图,设三角形及其中点如图所示,
则由三角形中位线定理可得:
DE= BC,DF= AC,EF= AB,
∵AB +BC +AC=8cm+10cm+12cm=20cm.
∴DE +DF +EF=10cm(三角形中位线等于底边一半).
∴各边中点为顶点的三角形的周长为10cm.
F
A
B
C
D
E
四、 典例精讲
1.已知直角三角形的两条直角边长分别为6和8,则连接
这两条直角边中点的线段长为 ( ).
A.3 B.4 C.5 D.6
C
五、 课堂练习
2.如图,D,E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD的度数是( ).
A.42° B.48° C.52° D.58°
B
五、 课堂练习
1.通过动手活动对获得的定理给予了直观的感受,为今后解决有关三角形中位线的问题提供了丰富的理论依据.
(1)三角形中位线平行于底边.
(2)三角形中位线等于底边的一半.
2.体会了证明命题的严格的要求,体会了证明的必要性.
六、 课堂小结
再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
