北师大版数学八下6.4《多边形的内角和与外角和第2课时》教学课件(共19张PPT)
文档属性
| 名称 | 北师大版数学八下6.4《多边形的内角和与外角和第2课时》教学课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 590.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 00:00:00 | ||
图片预览





文档简介
6.4 多边形内角和与外角和
第2课时
第六章 平行四边形
一、 学习目标
1.经历探索多边形外角和公式的过程,进一步发展合情推理能力。
2. 掌握多边形外角和公式,进一步发展演绎推理能力。
小刚住的小区有一个五边形的小道,小明绕各顶点走了一圈,回到起点A,并面对他出发时的方向,他的身体旋转了多少度?今天就让我们一起来探究一下.
二、 情境导入
(1)小刚从一个跑道运动到下一个跑道时,转过的角是哪个角?请标出.
(2)小刚跑完一圈,转过的角度之和是多少?
(3)你能求出一圈内小刚转过的角度之和吗?你是怎样计算的?
二、 情境导入
1.听一听:
一般的,在对多边形的任一顶点处按逆(顺)时针方向延长一边形成的新角叫做外角,那么n边形有2n个外角.
这样,任意一个多边形(含三边及以上)就含有两种角度;内角和外角.且相应的内角和外角互为邻补角,即两角之和为一平角.
三、 探究新知
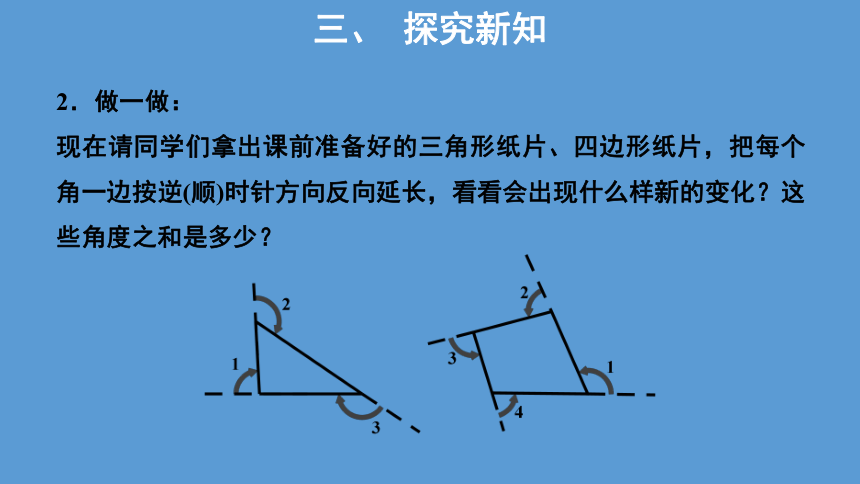
2.做一做:
现在请同学们拿出课前准备好的三角形纸片、四边形纸片,把每个角一边按逆(顺)时针方向反向延长,看看会出现什么样新的变化?这些角度之和是多少?
三、 探究新知
三、 探究新知
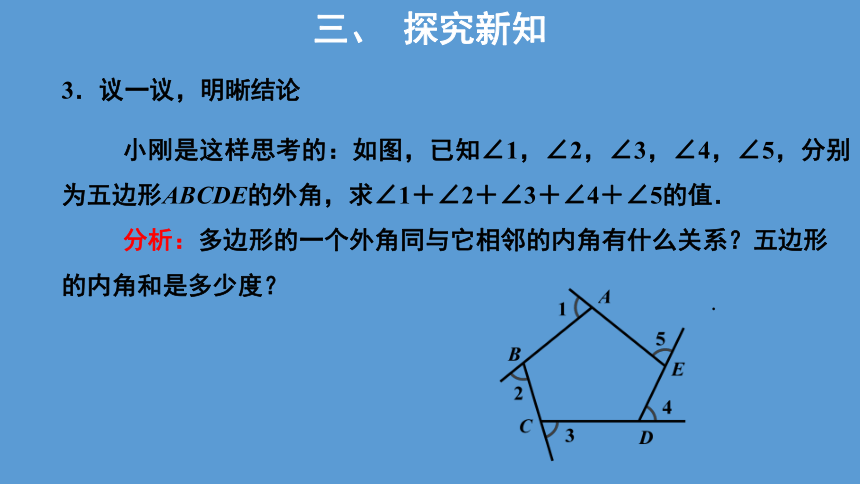
3.议一议,明晰结论
小刚是这样思考的:如图,已知∠1,∠2,∠3,∠4,∠5,分别为五边形ABCDE的外角,求∠1+∠2+∠3+∠4+∠5的值.
分析:多边形的一个外角同与它相邻的内角有什么关系?五边形的内角和是多少度?
解:∵∠1+∠EAB=180°,
∠2+∠ABC=180°,
∠3+∠BCD=180°,
∠4+∠CDE=180°,
∠5+∠DEA=180°,
∴∠1+∠EAB+∠2+∠ABC+∠3+∠BCD+∠4+∠CDE+∠5+∠DEA=5×180°.
A
B
C
D
E
1
2
3
4
5
三、 探究新知
又∠EAB+∠ABC+∠BCD+∠CDE+∠DEA
=(5-2)×180°,
∴∠1+∠2+∠3+∠4+∠5
=5×180°-(5-2)×180°
=360°.
这就是说,五边形的外角和为360°.
A
B
C
D
E
1
2
3
4
5
三、 探究新知
如果把五边形换成n边形呢?
因为n边形的每个内角与它相邻的外角是邻补角,它们的和是180°,所以n边形内角和加外角和等于n·180°,又因为n边形的内角和为(n-2)×180°所以,n边形的外角和为:n·180°-(n-2)·180°=360°.
三、 探究新知
结论:多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
多边形的外角和等于360゜.
三、 探究新知
四、典例精讲
例1 一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是(n-2)·180゜,
外角和等于360゜.
根据题意,得
(n-2)·180゜=3×360゜.
解得n=8.
所以,这个多边形是八边形.
四、 典例精讲
例2 正多边形的一个内角等于135°,则该多边形是正几边形?
解:设这个多边形是n边形,则它的内角和是(n-2)·180゜,
根据题意,得
(n-2)·180゜=135゜n.
解得n=8.
所以,这个多边形是八边形.
方法一
四、 典例精讲
例2 正多边形的一个内角等于135°,则该多边形是正几边形?
方法二
分析:n边形外角和等于360゜,正多边形的每个内角都相等,每个外角都相等,同一顶点的内角与外角互补。
解:每个外角的度数为180°—135°=45°,外角的个数为:360°÷45°=8
所以,这个多边形是八边形
1.多边形的内角和为外角和的4倍,这个多边形是( ).
A.八边形 B.九边形
C.十边形 D.十一边形
C
2.正多边形的一个外角等于36°,则该多边形是正( )
A.八边形 B.九边形
C.十边形 D.十一边形
C
五、 课堂练习
3.一个正多边形的内角和是540゜,则这个正多边形的每一个外角等于( ).
A.60゜ B.72゜ C.90゜ D.108゜
4.一个多边形的内角和与外角和的和为540°,则它是( )
A.五边形 B.四边形
C.三角形 D.不能确定
B
五、 课堂练习
C
六、 课堂小结
1.多边形的内角和等于(n-2)·180°,多边形的外角和等于360°.
2.多边形的边数与内角和、外角和的关系:
(1)n边形的内角和等于(n-2)·180°(n≥3,n是正整数),可见多边形内角和与边数n有关,每增加1条边,内角和增加180°.
(2)多边形的外角和等于360°,与边数的多少无关.
3.正n边形:正n边形的内角的度数为,外角的度数为
.
再见
第2课时
第六章 平行四边形
一、 学习目标
1.经历探索多边形外角和公式的过程,进一步发展合情推理能力。
2. 掌握多边形外角和公式,进一步发展演绎推理能力。
小刚住的小区有一个五边形的小道,小明绕各顶点走了一圈,回到起点A,并面对他出发时的方向,他的身体旋转了多少度?今天就让我们一起来探究一下.
二、 情境导入
(1)小刚从一个跑道运动到下一个跑道时,转过的角是哪个角?请标出.
(2)小刚跑完一圈,转过的角度之和是多少?
(3)你能求出一圈内小刚转过的角度之和吗?你是怎样计算的?
二、 情境导入
1.听一听:
一般的,在对多边形的任一顶点处按逆(顺)时针方向延长一边形成的新角叫做外角,那么n边形有2n个外角.
这样,任意一个多边形(含三边及以上)就含有两种角度;内角和外角.且相应的内角和外角互为邻补角,即两角之和为一平角.
三、 探究新知
2.做一做:
现在请同学们拿出课前准备好的三角形纸片、四边形纸片,把每个角一边按逆(顺)时针方向反向延长,看看会出现什么样新的变化?这些角度之和是多少?
三、 探究新知
三、 探究新知
3.议一议,明晰结论
小刚是这样思考的:如图,已知∠1,∠2,∠3,∠4,∠5,分别为五边形ABCDE的外角,求∠1+∠2+∠3+∠4+∠5的值.
分析:多边形的一个外角同与它相邻的内角有什么关系?五边形的内角和是多少度?
解:∵∠1+∠EAB=180°,
∠2+∠ABC=180°,
∠3+∠BCD=180°,
∠4+∠CDE=180°,
∠5+∠DEA=180°,
∴∠1+∠EAB+∠2+∠ABC+∠3+∠BCD+∠4+∠CDE+∠5+∠DEA=5×180°.
A
B
C
D
E
1
2
3
4
5
三、 探究新知
又∠EAB+∠ABC+∠BCD+∠CDE+∠DEA
=(5-2)×180°,
∴∠1+∠2+∠3+∠4+∠5
=5×180°-(5-2)×180°
=360°.
这就是说,五边形的外角和为360°.
A
B
C
D
E
1
2
3
4
5
三、 探究新知
如果把五边形换成n边形呢?
因为n边形的每个内角与它相邻的外角是邻补角,它们的和是180°,所以n边形内角和加外角和等于n·180°,又因为n边形的内角和为(n-2)×180°所以,n边形的外角和为:n·180°-(n-2)·180°=360°.
三、 探究新知
结论:多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
多边形的外角和等于360゜.
三、 探究新知
四、典例精讲
例1 一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是(n-2)·180゜,
外角和等于360゜.
根据题意,得
(n-2)·180゜=3×360゜.
解得n=8.
所以,这个多边形是八边形.
四、 典例精讲
例2 正多边形的一个内角等于135°,则该多边形是正几边形?
解:设这个多边形是n边形,则它的内角和是(n-2)·180゜,
根据题意,得
(n-2)·180゜=135゜n.
解得n=8.
所以,这个多边形是八边形.
方法一
四、 典例精讲
例2 正多边形的一个内角等于135°,则该多边形是正几边形?
方法二
分析:n边形外角和等于360゜,正多边形的每个内角都相等,每个外角都相等,同一顶点的内角与外角互补。
解:每个外角的度数为180°—135°=45°,外角的个数为:360°÷45°=8
所以,这个多边形是八边形
1.多边形的内角和为外角和的4倍,这个多边形是( ).
A.八边形 B.九边形
C.十边形 D.十一边形
C
2.正多边形的一个外角等于36°,则该多边形是正( )
A.八边形 B.九边形
C.十边形 D.十一边形
C
五、 课堂练习
3.一个正多边形的内角和是540゜,则这个正多边形的每一个外角等于( ).
A.60゜ B.72゜ C.90゜ D.108゜
4.一个多边形的内角和与外角和的和为540°,则它是( )
A.五边形 B.四边形
C.三角形 D.不能确定
B
五、 课堂练习
C
六、 课堂小结
1.多边形的内角和等于(n-2)·180°,多边形的外角和等于360°.
2.多边形的边数与内角和、外角和的关系:
(1)n边形的内角和等于(n-2)·180°(n≥3,n是正整数),可见多边形内角和与边数n有关,每增加1条边,内角和增加180°.
(2)多边形的外角和等于360°,与边数的多少无关.
3.正n边形:正n边形的内角的度数为,外角的度数为
.
再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
