北师大版八年级数学下册4.3公式法 第1课时 教学课件(共25张PPT)
文档属性
| 名称 | 北师大版八年级数学下册4.3公式法 第1课时 教学课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 00:00:00 | ||
图片预览







文档简介
4.3 公式法
第1课时
第四章 因式分解
一、 学习目标
1.经历通过整式乘法公式(a+b)(a-b)= a2-b2 的逆向变形得出公式法因式分解的方法的过程,发展逆向思维和推理能力。
2. 会用平方差公式分解因式。
问题1:请同学们观察多项式x2-25,9x2-y2,它们有什么共同的特征?
答:因为多项式x2-25,9x2-y2,可分别化为x2-52和(3x)2-y2的形式,所以它们的共同特征是:都是两个数平方差的形式.
二、 情境导入
问题2:尝试将它们分别写成两个因式的乘积,并与同伴交流.
答:多项式x2-25,9x2-y2的共同特征都是两项,且都是差的形式,各项都能写成平方的形式:x2-25=x2-52=(x+5)(x-5);9x2-y2=(3x)2-y2=(3x+y)(3x-y).
二、 情境导入
事实上把乘法公式(a+b)(a-b)= a2-b2反过来,就得到平方差公式a2-b2=(a+b)(a-b).
二、 情境导入
1.平方差公式的再认识
问题1:上面我们将一个具备一定特征的多项式进行了分解因式,这里的特征就是该多项式是两项差式,各项都能够写成平方形式.
现在你能结合平方差公式具体谈谈它的用途吗?
三、 探究新知
公式 ,从左向右用来处理特殊的整式乘法,而由右向左则用来处理特殊多项式的分解因式问题.由此可以又进一步体会到整式乘法与因式分解的互逆过程.
三、 探究新知
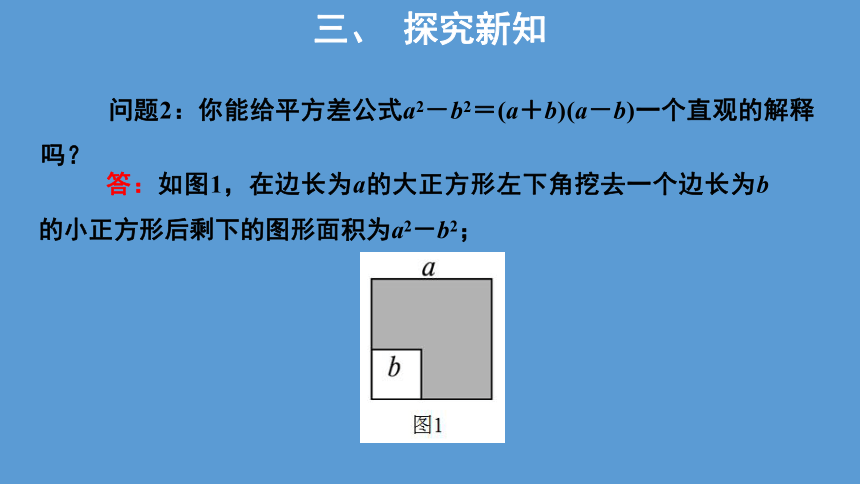
问题2:你能给平方差公式a2-b2=(a+b)(a-b)一个直观的解释吗?
答:如图1,在边长为a的大正方形左下角挖去一个边长为b的小正方形后剩下的图形面积为a2-b2;
三、 探究新知
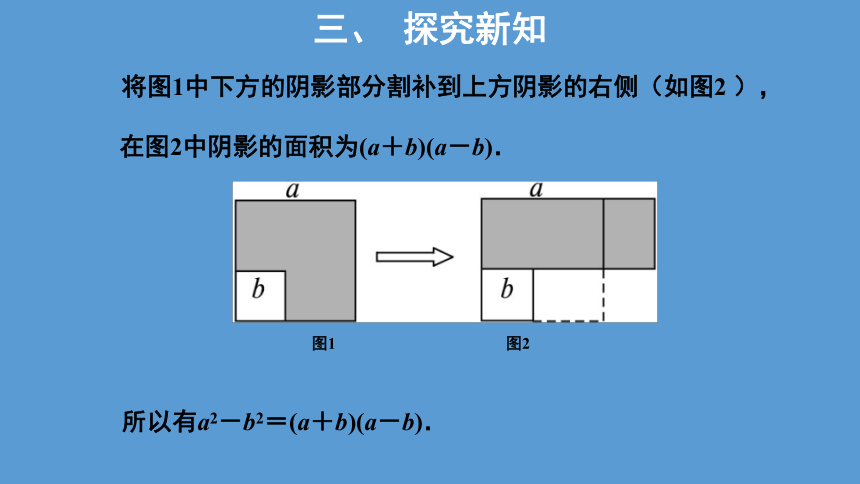
将图1中下方的阴影部分割补到上方阴影的右侧(如图2 ),
图1 图2
所以有a2-b2=(a+b)(a-b).
在图2中阴影的面积为(a+b)(a-b).
三、 探究新知
(2)9a2- =(3a)2-( b)2=(3a+ b)(3a- b).
例1 分解因式:(1)25-16x2;(2) 9a2-
解:(1)25-16x2=52-(4x)2=(5+4x)(5-4x);
点评:本题是把一个多项式的两项都化成两个单项式的平方,再利用平方差公式分解因式;在(1)中公式中的a指代5,b指代4x;在(2)中公式中的a指代3a,b指代 b.
四、 典例精讲
例2 把下列各式分解因式:
(1)9(m+n)2-(m-n)2;(2)2x3-8x.
解:(1)9(m+n)2-(m-n)2=[3(m+n)]2-(m-n)2
=[3(m+n)+(m-n)][3(m+n)-(m-n)]
=(3m+3n+m-n)(3m+3n-m+n)
=(4m+2n)(2m+4n)
=4(2m+n)(m+2n).
四、 典例精讲
(2)2x3-8x=2x(x2-4)=2x(x+2)(x-2).
点评:本题的(1)是把一个二项式化成两个多项式的平方差,然后借助于整体方法使用平方差公式分解因式,公式中的a在这里指代的是3(m+n),b指代的是m-n;
四、 典例精讲
(2)是先提公因式,然后再用平方差公式分解因式,由此可知,当一个题中既要用提公因式法,又要用公式法分解因式时,首先要考虑提公因式法,再考虑公式法.
四、 典例精讲
例3 判断下列分解因式是否正确.错误的加以改正.
(1)(a+b)2-c2=a2+2ab+b2-c2.
解:不正确.
本题错在对分解因式的概念不清,左边是多项式的形式,右边应是整式乘积的形式,但(1)中还是多项式的形式,因此,最终结果未对所给多项式进行因式分解,而是典型的整式乘法化简题,正确应为:(a+b)2-c2=(a+b+c)(a+b-c).
四、 典例精讲
解:不正确.
错误原因是因式分解不彻底,因为a2-1还能继续分解成(a+1)(a-1).正确解答应为
a4-1=(a2+1)(a2-1)=(a2+1)(a+1)(a-1).
例3 判断下列分解因式是否正确.错误的加以改正.
(2)a4-1=(a2)2-1=(a2+1)·(a2-1).
四、 典例精讲
1.判断正误.
(1)x2+y2=(x+y)(x-y ) ; ( )
(2)x2-y2=(x+y)(x-y); ( )
(3)-x2+y2=(-x+y)(-x-y); ( )
(4)-x2-y2=-(x+y)(x-y). ( )
×
×
×
√
五、 课堂练习
2.把下列各式分解因式.
(1)a2b2-m2;(2)(m-a)2-(n+b)2;
(3)x2-(a+b-c)2;(4)-16x4+81y4.
解:(1)a2b2-m2=(ab)2-m2=(ab+m)(ab-m);
(2)(m-a)2-(n+b)2
=[(m-a)+(n+b)][(m-a)-(n+b)]
=(m-a+n+b)(m-a-n-b);
五、 课堂练习
(3)x2-(a+b-c)2
=[x+(a+b-c)][x-(a+b-c)]
=(x+a+b-c)(x-a-b+c);
(4)-16x4+81y4
=(9y2)2-(4x2)2
=(9y2+4x2)(9y2-4x2)
=(9y2+4x2)(3y+2x)(3y-2x).
五、 课堂练习
3.把下列各式因式分解:
(1)36(x+y)2-49(x-y)2;
解:36(x+y)2-49(x-y)2
=[6(x+y)]2-[7(x-y)]2
=[6(x+y)+7(x-y)][6(x+y)-7(x-y)]
=(6x+6y+7x-7y)(6x+6y-7x+7y)
=(13x-y)(13y-x);
五、 课堂练习
3.把下列各式因式分解:
(2)(x-1)+b2(1-x);
解:(x-1)+b2(1-x)=(x-1)-b2(x-1)
=(x-1)(1-b2)
=(x-1)(1+b)(1-b);
五、 课堂练习
3.把下列各式因式分解:
(3)(x2+x+1)2-1.
解:(x2+x+1)2-1
=(x2+x+1+1)(x2+x+1-1)
=(x2+x+2)(x2+x)
=x(x+1)(x2+x+2).
五、 课堂练习
1.我们已学习过的因式分解方法有提公因式法和运用平方差公式法.如果多项式各项含有公因式,则第一步是提公因式,然后看是否符合平方差公式的结构特点,若符合则继续进行.
第一步分解因式以后,所含的多项式还可以继续分解,则需要进一步分解因式,直到每个多项式都不能分解为止.
六、 课堂小结
2.分解因式的一般程序:
(1)观察.观察多项式的结构特征,明确下一步的方向.
(2)提取公因式.有公因式的先提取出来,为下一步做好准备.
(3)使用平方差公式继续分解.
(4)分解因式的最终结果必须彻底到位.
六、 课堂小结
再见
第1课时
第四章 因式分解
一、 学习目标
1.经历通过整式乘法公式(a+b)(a-b)= a2-b2 的逆向变形得出公式法因式分解的方法的过程,发展逆向思维和推理能力。
2. 会用平方差公式分解因式。
问题1:请同学们观察多项式x2-25,9x2-y2,它们有什么共同的特征?
答:因为多项式x2-25,9x2-y2,可分别化为x2-52和(3x)2-y2的形式,所以它们的共同特征是:都是两个数平方差的形式.
二、 情境导入
问题2:尝试将它们分别写成两个因式的乘积,并与同伴交流.
答:多项式x2-25,9x2-y2的共同特征都是两项,且都是差的形式,各项都能写成平方的形式:x2-25=x2-52=(x+5)(x-5);9x2-y2=(3x)2-y2=(3x+y)(3x-y).
二、 情境导入
事实上把乘法公式(a+b)(a-b)= a2-b2反过来,就得到平方差公式a2-b2=(a+b)(a-b).
二、 情境导入
1.平方差公式的再认识
问题1:上面我们将一个具备一定特征的多项式进行了分解因式,这里的特征就是该多项式是两项差式,各项都能够写成平方形式.
现在你能结合平方差公式具体谈谈它的用途吗?
三、 探究新知
公式 ,从左向右用来处理特殊的整式乘法,而由右向左则用来处理特殊多项式的分解因式问题.由此可以又进一步体会到整式乘法与因式分解的互逆过程.
三、 探究新知
问题2:你能给平方差公式a2-b2=(a+b)(a-b)一个直观的解释吗?
答:如图1,在边长为a的大正方形左下角挖去一个边长为b的小正方形后剩下的图形面积为a2-b2;
三、 探究新知
将图1中下方的阴影部分割补到上方阴影的右侧(如图2 ),
图1 图2
所以有a2-b2=(a+b)(a-b).
在图2中阴影的面积为(a+b)(a-b).
三、 探究新知
(2)9a2- =(3a)2-( b)2=(3a+ b)(3a- b).
例1 分解因式:(1)25-16x2;(2) 9a2-
解:(1)25-16x2=52-(4x)2=(5+4x)(5-4x);
点评:本题是把一个多项式的两项都化成两个单项式的平方,再利用平方差公式分解因式;在(1)中公式中的a指代5,b指代4x;在(2)中公式中的a指代3a,b指代 b.
四、 典例精讲
例2 把下列各式分解因式:
(1)9(m+n)2-(m-n)2;(2)2x3-8x.
解:(1)9(m+n)2-(m-n)2=[3(m+n)]2-(m-n)2
=[3(m+n)+(m-n)][3(m+n)-(m-n)]
=(3m+3n+m-n)(3m+3n-m+n)
=(4m+2n)(2m+4n)
=4(2m+n)(m+2n).
四、 典例精讲
(2)2x3-8x=2x(x2-4)=2x(x+2)(x-2).
点评:本题的(1)是把一个二项式化成两个多项式的平方差,然后借助于整体方法使用平方差公式分解因式,公式中的a在这里指代的是3(m+n),b指代的是m-n;
四、 典例精讲
(2)是先提公因式,然后再用平方差公式分解因式,由此可知,当一个题中既要用提公因式法,又要用公式法分解因式时,首先要考虑提公因式法,再考虑公式法.
四、 典例精讲
例3 判断下列分解因式是否正确.错误的加以改正.
(1)(a+b)2-c2=a2+2ab+b2-c2.
解:不正确.
本题错在对分解因式的概念不清,左边是多项式的形式,右边应是整式乘积的形式,但(1)中还是多项式的形式,因此,最终结果未对所给多项式进行因式分解,而是典型的整式乘法化简题,正确应为:(a+b)2-c2=(a+b+c)(a+b-c).
四、 典例精讲
解:不正确.
错误原因是因式分解不彻底,因为a2-1还能继续分解成(a+1)(a-1).正确解答应为
a4-1=(a2+1)(a2-1)=(a2+1)(a+1)(a-1).
例3 判断下列分解因式是否正确.错误的加以改正.
(2)a4-1=(a2)2-1=(a2+1)·(a2-1).
四、 典例精讲
1.判断正误.
(1)x2+y2=(x+y)(x-y ) ; ( )
(2)x2-y2=(x+y)(x-y); ( )
(3)-x2+y2=(-x+y)(-x-y); ( )
(4)-x2-y2=-(x+y)(x-y). ( )
×
×
×
√
五、 课堂练习
2.把下列各式分解因式.
(1)a2b2-m2;(2)(m-a)2-(n+b)2;
(3)x2-(a+b-c)2;(4)-16x4+81y4.
解:(1)a2b2-m2=(ab)2-m2=(ab+m)(ab-m);
(2)(m-a)2-(n+b)2
=[(m-a)+(n+b)][(m-a)-(n+b)]
=(m-a+n+b)(m-a-n-b);
五、 课堂练习
(3)x2-(a+b-c)2
=[x+(a+b-c)][x-(a+b-c)]
=(x+a+b-c)(x-a-b+c);
(4)-16x4+81y4
=(9y2)2-(4x2)2
=(9y2+4x2)(9y2-4x2)
=(9y2+4x2)(3y+2x)(3y-2x).
五、 课堂练习
3.把下列各式因式分解:
(1)36(x+y)2-49(x-y)2;
解:36(x+y)2-49(x-y)2
=[6(x+y)]2-[7(x-y)]2
=[6(x+y)+7(x-y)][6(x+y)-7(x-y)]
=(6x+6y+7x-7y)(6x+6y-7x+7y)
=(13x-y)(13y-x);
五、 课堂练习
3.把下列各式因式分解:
(2)(x-1)+b2(1-x);
解:(x-1)+b2(1-x)=(x-1)-b2(x-1)
=(x-1)(1-b2)
=(x-1)(1+b)(1-b);
五、 课堂练习
3.把下列各式因式分解:
(3)(x2+x+1)2-1.
解:(x2+x+1)2-1
=(x2+x+1+1)(x2+x+1-1)
=(x2+x+2)(x2+x)
=x(x+1)(x2+x+2).
五、 课堂练习
1.我们已学习过的因式分解方法有提公因式法和运用平方差公式法.如果多项式各项含有公因式,则第一步是提公因式,然后看是否符合平方差公式的结构特点,若符合则继续进行.
第一步分解因式以后,所含的多项式还可以继续分解,则需要进一步分解因式,直到每个多项式都不能分解为止.
六、 课堂小结
2.分解因式的一般程序:
(1)观察.观察多项式的结构特征,明确下一步的方向.
(2)提取公因式.有公因式的先提取出来,为下一步做好准备.
(3)使用平方差公式继续分解.
(4)分解因式的最终结果必须彻底到位.
六、 课堂小结
再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
