人教版 八年级数学下册 第18章 平行四边形 课时训练(Word版含答案解析)
文档属性
| 名称 | 人教版 八年级数学下册 第18章 平行四边形 课时训练(Word版含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 437.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 13:28:27 | ||
图片预览

文档简介
人教版 八年级数学 第18章 平行四边形 课时训练
一、选择题
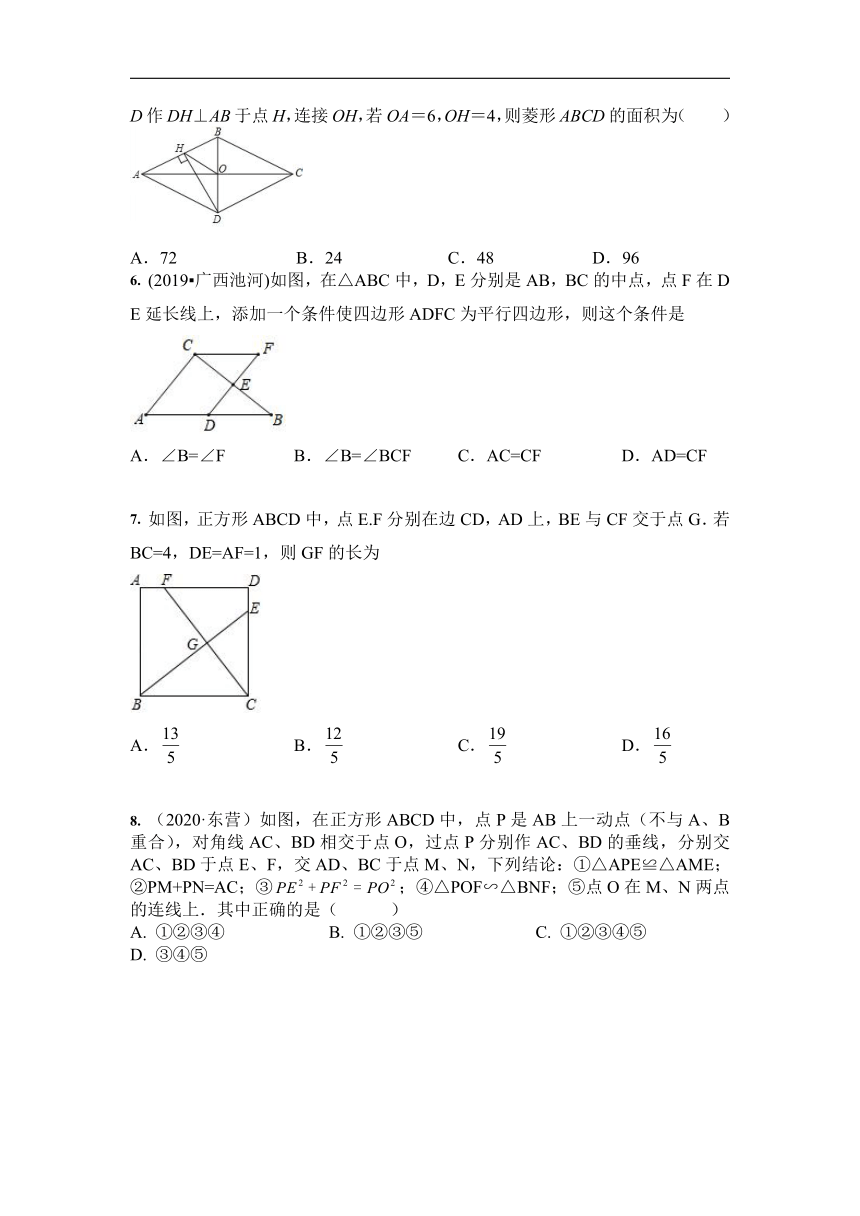
1. 如图,在菱形中,,,则菱形的边长为( )
A. B. C. D.
2. 如图,在菱形中,,、分别是边和的中点,于点,则( )
A. B. C. D.
3. 菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为( )
A. 2 B. 4 C. 6 D. 8
4. (2020·抚顺本溪辽阳)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,AC=8,BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2 B. C.3 D.4
5. (2020·黑龙江龙东)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
A.72 B.24 C.48 D.96
6. (2019?广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是
A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF
7. 如图,正方形ABCD中,点E.F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则GF的长为
A. B. C. D.
8. (2020·东营)如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N,下列结论:①△APE≌△AME;②PM+PN=AC;③;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是( )
A. ①②③④ B. ①②③⑤ C. ①②③④⑤ D. ③④⑤
二、填空题
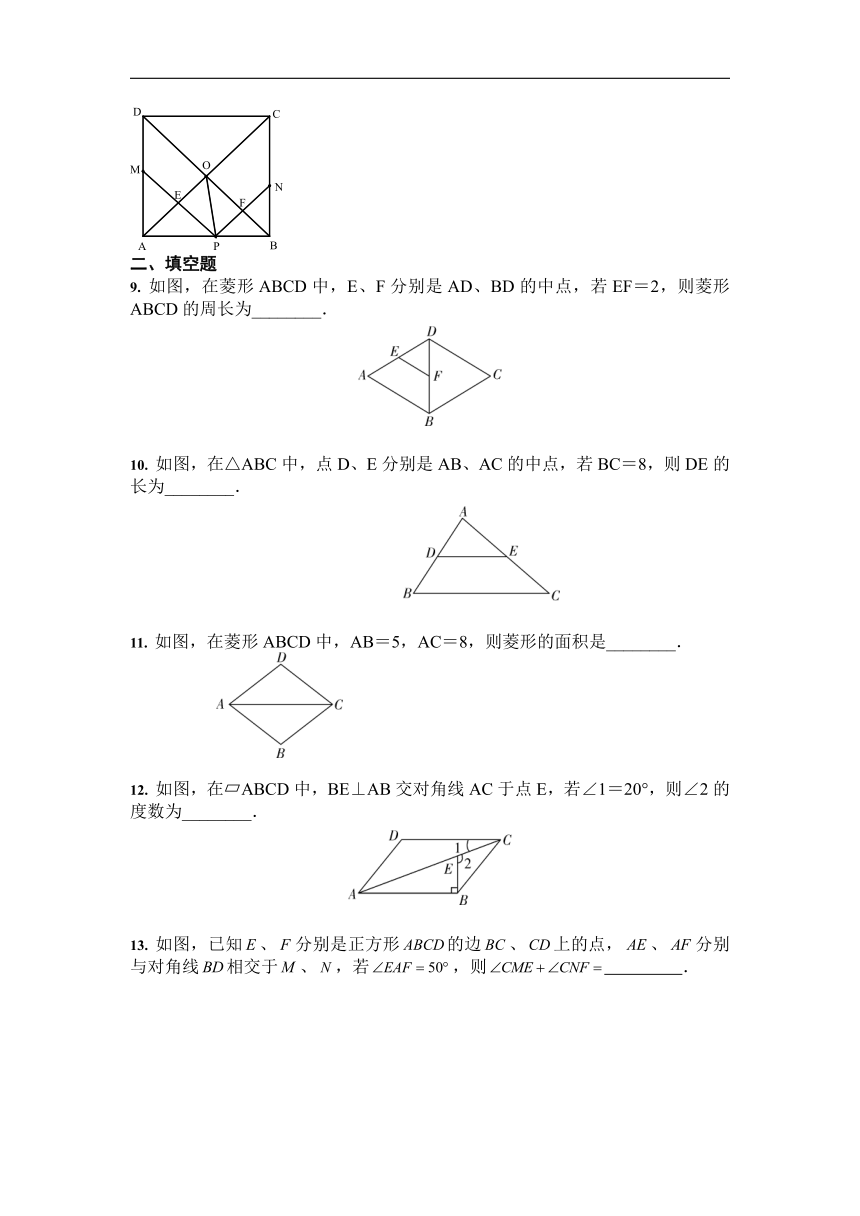
9. 如图,在菱形ABCD中,E、F分别是AD、BD的中点,若EF=2,则菱形ABCD的周长为________.
10. 如图,在△ABC中,点D、E分别是AB、AC的中点,若BC=8,则DE的长为________.
11. 如图,在菱形ABCD中,AB=5,AC=8,则菱形的面积是________.
12. 如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为________.
13. 如图,已知、分别是正方形的边、上的点,、分别与对角线相交于、,若,则 .
14. 如图,已知等边三角形的边长为,是内一点,,,点分别在上,则
15. 如图,ABCD的对角线AC、BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为__________.
三、解答题
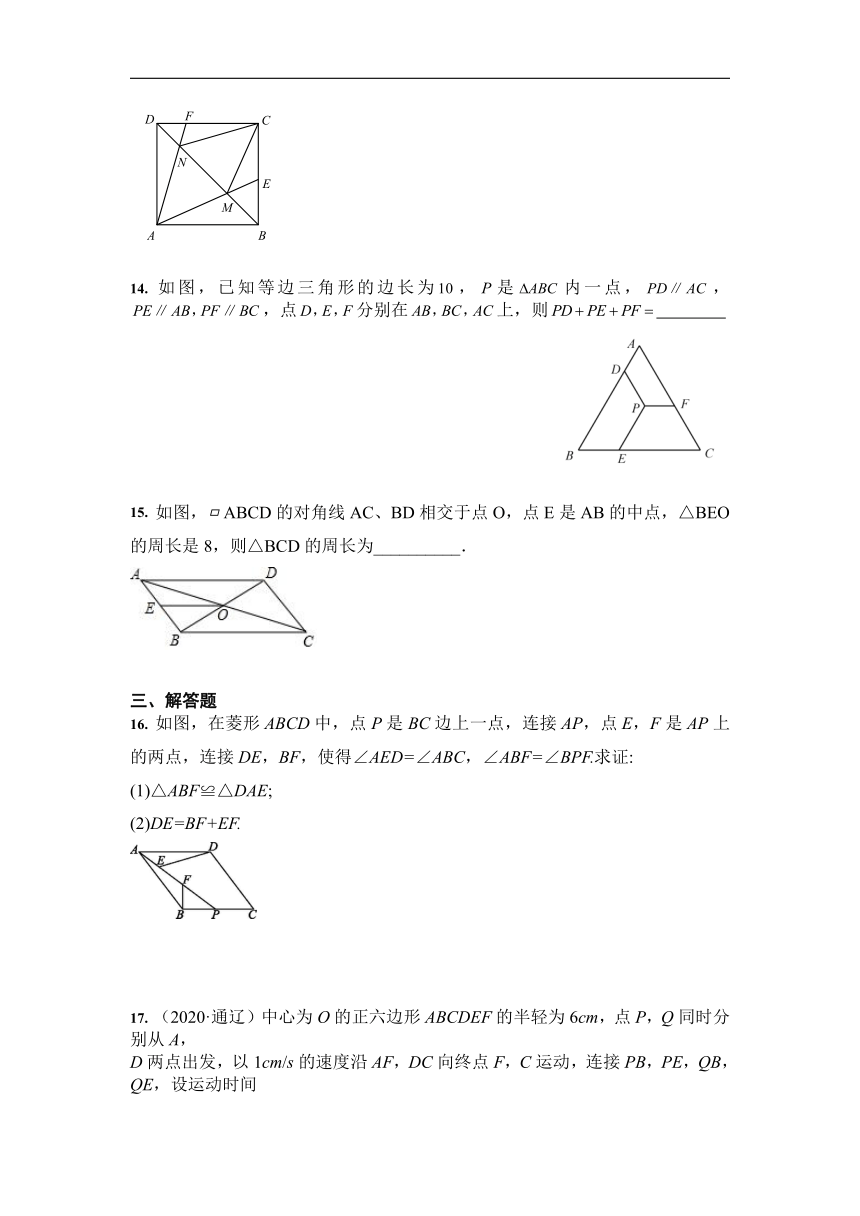
16. 如图,在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.求证:
(1)△ABF≌△DAE;
(2)DE=BF+EF.
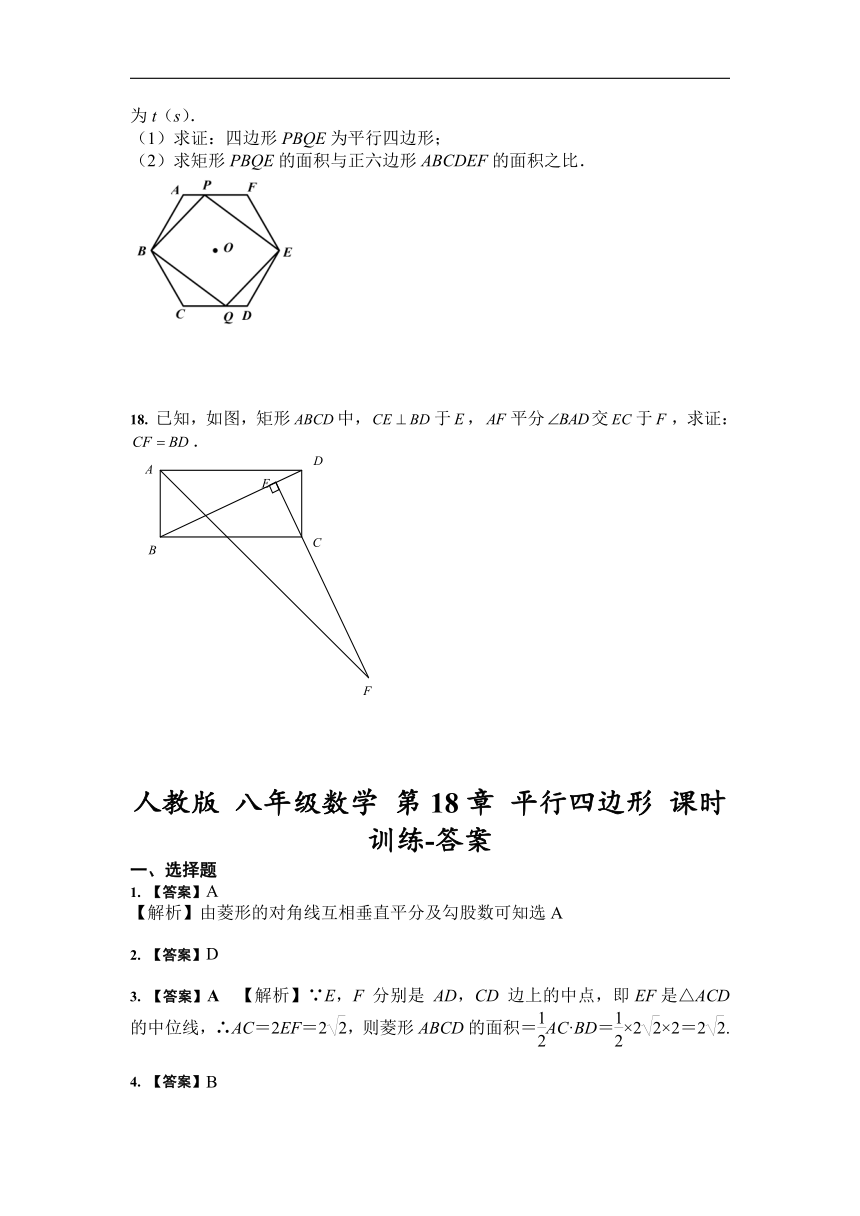
17. (2020·通辽)中心为O的正六边形ABCDEF的半轻为6cm,点P,Q同时分别从A,
D两点出发,以1cm/s的速度沿AF,DC向终点F,C运动,连接PB,PE,QB,QE,设运动时间
为t(s).
(1)求证:四边形PBQE为平行四边形;
(2)求矩形PBQE的面积与正六边形ABCDEF的面积之比.
18. 已知,如图,矩形中,于,平分交于,求证:.
人教版 八年级数学 第18章 平行四边形 课时训练-答案
一、选择题
1. 【答案】A
【解析】由菱形的对角线互相垂直平分及勾股数可知选A
2. 【答案】D
3. 【答案】A 【解析】∵E,F 分别是 AD,CD 边上的中点,即EF是△ACD的中位线,∴AC=2EF=2,则菱形ABCD的面积=AC·BD=×2×2=2.
4. 【答案】B
【解析】根据菱形对角线互相垂直平分,求出菱形的边长,再结合等腰三角形的性质及判定得出OE=CE=DE,从而求出.∵四边形ABCD是菱形,∴OC=AC=4, OD=BD=3, AC⊥DB.∵OE=CE,∴∠EOC=OE∠DCO.∵∠DOE+∠EOC=∠ODC+∠ECO=90°,∴∠DOE=∠ODC,∴OE=DE,∴OE=DC.在Rt△DOC中,CD==5,∴OE=DC=.故选项B正确.
5. 【答案】 C
【解析】本题考查了菱形的性质,对角线互相垂直平分以及直角三角形的斜边上中线的性质,解:∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD,
∵DH⊥AB,∴∠BHD=90°,∴BD=2OH,∵OH=4,∴BD=8,
∵OA=6,∴AC=12,∴菱形ABCD的面积.故选:C.
6. 【答案】B
【解析】∵在△ABC中,D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,∴DEAC.
A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.
C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.
故选B.
7. 【答案】A
【解析】正方形ABCD中,∵BC=4,
∴BC=CD=AD=4,∠BCE=∠CDF=90°,
∵AF=DE=1,∴DF=CE=3,∴BE=CF=5,
在△BCE和△CDF中,,
∴△BCE≌△CDF(SAS),∴∠CBE=∠DCF,
∵∠CBE+∠CEB=∠ECG+∠CEB=90°=∠CGE,
cos∠CBE=cos∠ECG=,
∴,CG=,∴GF=CF﹣CG=5﹣=,
故选A.
8. 【答案】B
【解析】本题考查了垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质,是常见问题的综合,灵活的运用所学知识是解答本题的关键.综合应用垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质等知识,逐个判断5个结论的正确性,得出结论.
①∵正方形ABCD,∴∠APE=∠AME=45°,∵PM⊥AE,∴∠AEP=∠AEM=90°,∵AE=AE,∴△APE≌△AME(ASA);
②过点N作NQ⊥AC于点Q,则四边形PNQE是矩形,∴PN=EQ,∵正方形ABCD,∴∠PAE=∠MAE=45°,∵PM⊥AE,∴∠PEA=45°,∴∠PAE=∠APE,PE=NQ,∴△APE等腰直角三角形,∴AE=PE,同理得:△NQC等腰直角三角形,∴NQ=CQ,∵△APE≌△AME,∴PE=ME,∴PE=ME= NQ=CQ,∴PM=AE+CQ,∴PM+PN=AE+CQ+EQ=AC,即PM+PN=AC成立;
③∵正方形ABCD,∴AC⊥BD,∴∠EOF是直角,∵过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,∴∠PEO和∠PFO是直角,∴四边形PFOE是矩形,∴PF=OE,在Rt△PEO中,有PE2+OE2=PO2,∴PE2+PF2=PO2,即PE2+PF2=PO2成立;
④△BNF是等腰直角三角形,点P不在AB的中点时,△POF不是等腰直角三角形,所以△POF与△BNF不一定相似,即△POF∽△BNF不一定成立;
⑤∵△AMP是等腰直角三角形,△PMN∽△AMP,∴△PMN是等腰直角三角形,∵∠MPN=90°,∴PM=PN,∵AP=PM,BP=PN,∴AP=BP,∴点P是AB的中点,又∵O为正方形的对称中点,∴点O在M、N两点的连线上.综上,①②③⑤成立,即正确的结论有4个,答案选B.
二、填空题
9. 【答案】16 【解析】∵E,F分别是AD,BD的中点,∴AB=2EF=4,∴菱形ABCD周长是4AB=16.
10. 【答案】4 【解析】∵点D、E分别是AB、AC的中点,∴由三角形的中位线定理可知DE=BC=4.
11. 【答案】24 【解析】如解图,连接BD交AC于点O,∵四边形ABCD是菱形,AB=5,AC=8,且菱形的对角线互相垂直平分,∴OA=4,在Rt△AOB中,由勾股定理得OB=3,∴BD=6,∴S菱形ABCD=AC·BD=×8×6=24.
解图
12. 【答案】110° 【解析】 ∵四边形ABCD是平行四边形,∴CD∥AB,∴∠CAB=∠1=20°,∵BE ⊥AB交对角线AC于点E,∴∠ABE=90°,∴∠2=∠CAB+∠ABE=20°+90°=110°.
13. 【答案】
【解析】如图,连结.
14. 【答案】
15. 【答案】16
【解析】∵ABCD的对角线AC、BD相交于点O,
∴BO=DO=BD,BD=2OB,∴O为BD中点,
∵点E是AB的中点,∴AB=2BE,BC=2OE,
∵四边形ABCD是平行四边形,∴AB=CD,∴CD=2BE.
∵△BEO的周长为8,∴OB+OE+BE=8,
∴BD+BC+CD=2OB+2OE+2BE=2(OB+OE+BE)=16,
∴△BCD的周长是16,故答案为16.
三、解答题
16. 【答案】
证明:(1)∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,∴∠BPA=∠DAE.
在△ABP和△DAE中,又∵∠ABC=∠AED,∴∠BAF=∠ADE.
∵∠ABF=∠BPF,∠BPA=∠DAE,
∴∠ABF=∠DAE,
又∵AB=DA,∴△ABF≌△DAE(ASA).
(2)∵△ABF≌△DAE,∴AE=BF,DE=AF.
∵AF=AE+EF=BF+EF,
∴DE=BF+EF.
17. 【答案】
证明:(1)在正六边形ABCDEF中,AB=AF=FE=ED=DC=BC=6,∠A=∠F=∠D=∠C=120°,
∵VP=VQ=1cm/s,∴AP=DQ=t,
∵PF=AF-AP=6-t,CQ=CD-DQ=6-t,
∴PF=CQ=6-t,
在△ABP和△DQE中,
AP=DQ=t,∠A =∠D =120°,AB=DE=6,
∴△ABP≌△DQE,∴BP=EQ,
同理可证△PEF≌△QBC,∴PE=QB,
∴四边形PBQE为平行四边形.
(2)连结BE,CO,DO,作CG⊥BE于点G,QH⊥BE于点H.
∵四边形PBQE是矩形,∴∠BQE=90°,
∴BE是正六边形ABCDEF的外接圆直径,
即BE过点O,且BE=12,
∵ED=DC=BC=6,
∴∠EOD=∠COD=∠BOC =60°,
又∵OE=OD=OC=OB,
∴△EOD,△COD,△BOC是全等的等边三角形,
∴CG=CO·sin∠BOC=CO·sin60°=6×=,
∴S△DOE= S△COD= S△BOC=BO·CG=×6×=,
∵∠BCD+∠CBO=180°,∴CD∥BE,
∵CG⊥BE,QH⊥BE,
∴QH=CG=,
∴S△BEQ=BE·QH=×12×=,
∵正六边形ABCDEF是以直线BE为对称轴的轴对称图形,矩形PBQE关于点O成中心对称,
∴===.
18. 【答案】
连结交于,∵四边形为矩形,∴,
∴,∴
∵平分,
∴,
∴
∵,
∴
∵,∴,
∴,
∴,
∴
一、选择题
1. 如图,在菱形中,,,则菱形的边长为( )
A. B. C. D.
2. 如图,在菱形中,,、分别是边和的中点,于点,则( )
A. B. C. D.
3. 菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为( )
A. 2 B. 4 C. 6 D. 8
4. (2020·抚顺本溪辽阳)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,AC=8,BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2 B. C.3 D.4
5. (2020·黑龙江龙东)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
A.72 B.24 C.48 D.96
6. (2019?广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是
A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF
7. 如图,正方形ABCD中,点E.F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则GF的长为
A. B. C. D.
8. (2020·东营)如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N,下列结论:①△APE≌△AME;②PM+PN=AC;③;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是( )
A. ①②③④ B. ①②③⑤ C. ①②③④⑤ D. ③④⑤
二、填空题
9. 如图,在菱形ABCD中,E、F分别是AD、BD的中点,若EF=2,则菱形ABCD的周长为________.
10. 如图,在△ABC中,点D、E分别是AB、AC的中点,若BC=8,则DE的长为________.
11. 如图,在菱形ABCD中,AB=5,AC=8,则菱形的面积是________.
12. 如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为________.
13. 如图,已知、分别是正方形的边、上的点,、分别与对角线相交于、,若,则 .
14. 如图,已知等边三角形的边长为,是内一点,,,点分别在上,则
15. 如图,ABCD的对角线AC、BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为__________.
三、解答题
16. 如图,在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.求证:
(1)△ABF≌△DAE;
(2)DE=BF+EF.
17. (2020·通辽)中心为O的正六边形ABCDEF的半轻为6cm,点P,Q同时分别从A,
D两点出发,以1cm/s的速度沿AF,DC向终点F,C运动,连接PB,PE,QB,QE,设运动时间
为t(s).
(1)求证:四边形PBQE为平行四边形;
(2)求矩形PBQE的面积与正六边形ABCDEF的面积之比.
18. 已知,如图,矩形中,于,平分交于,求证:.
人教版 八年级数学 第18章 平行四边形 课时训练-答案
一、选择题
1. 【答案】A
【解析】由菱形的对角线互相垂直平分及勾股数可知选A
2. 【答案】D
3. 【答案】A 【解析】∵E,F 分别是 AD,CD 边上的中点,即EF是△ACD的中位线,∴AC=2EF=2,则菱形ABCD的面积=AC·BD=×2×2=2.
4. 【答案】B
【解析】根据菱形对角线互相垂直平分,求出菱形的边长,再结合等腰三角形的性质及判定得出OE=CE=DE,从而求出.∵四边形ABCD是菱形,∴OC=AC=4, OD=BD=3, AC⊥DB.∵OE=CE,∴∠EOC=OE∠DCO.∵∠DOE+∠EOC=∠ODC+∠ECO=90°,∴∠DOE=∠ODC,∴OE=DE,∴OE=DC.在Rt△DOC中,CD==5,∴OE=DC=.故选项B正确.
5. 【答案】 C
【解析】本题考查了菱形的性质,对角线互相垂直平分以及直角三角形的斜边上中线的性质,解:∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD,
∵DH⊥AB,∴∠BHD=90°,∴BD=2OH,∵OH=4,∴BD=8,
∵OA=6,∴AC=12,∴菱形ABCD的面积.故选:C.
6. 【答案】B
【解析】∵在△ABC中,D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,∴DEAC.
A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.
C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.
故选B.
7. 【答案】A
【解析】正方形ABCD中,∵BC=4,
∴BC=CD=AD=4,∠BCE=∠CDF=90°,
∵AF=DE=1,∴DF=CE=3,∴BE=CF=5,
在△BCE和△CDF中,,
∴△BCE≌△CDF(SAS),∴∠CBE=∠DCF,
∵∠CBE+∠CEB=∠ECG+∠CEB=90°=∠CGE,
cos∠CBE=cos∠ECG=,
∴,CG=,∴GF=CF﹣CG=5﹣=,
故选A.
8. 【答案】B
【解析】本题考查了垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质,是常见问题的综合,灵活的运用所学知识是解答本题的关键.综合应用垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质等知识,逐个判断5个结论的正确性,得出结论.
①∵正方形ABCD,∴∠APE=∠AME=45°,∵PM⊥AE,∴∠AEP=∠AEM=90°,∵AE=AE,∴△APE≌△AME(ASA);
②过点N作NQ⊥AC于点Q,则四边形PNQE是矩形,∴PN=EQ,∵正方形ABCD,∴∠PAE=∠MAE=45°,∵PM⊥AE,∴∠PEA=45°,∴∠PAE=∠APE,PE=NQ,∴△APE等腰直角三角形,∴AE=PE,同理得:△NQC等腰直角三角形,∴NQ=CQ,∵△APE≌△AME,∴PE=ME,∴PE=ME= NQ=CQ,∴PM=AE+CQ,∴PM+PN=AE+CQ+EQ=AC,即PM+PN=AC成立;
③∵正方形ABCD,∴AC⊥BD,∴∠EOF是直角,∵过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,∴∠PEO和∠PFO是直角,∴四边形PFOE是矩形,∴PF=OE,在Rt△PEO中,有PE2+OE2=PO2,∴PE2+PF2=PO2,即PE2+PF2=PO2成立;
④△BNF是等腰直角三角形,点P不在AB的中点时,△POF不是等腰直角三角形,所以△POF与△BNF不一定相似,即△POF∽△BNF不一定成立;
⑤∵△AMP是等腰直角三角形,△PMN∽△AMP,∴△PMN是等腰直角三角形,∵∠MPN=90°,∴PM=PN,∵AP=PM,BP=PN,∴AP=BP,∴点P是AB的中点,又∵O为正方形的对称中点,∴点O在M、N两点的连线上.综上,①②③⑤成立,即正确的结论有4个,答案选B.
二、填空题
9. 【答案】16 【解析】∵E,F分别是AD,BD的中点,∴AB=2EF=4,∴菱形ABCD周长是4AB=16.
10. 【答案】4 【解析】∵点D、E分别是AB、AC的中点,∴由三角形的中位线定理可知DE=BC=4.
11. 【答案】24 【解析】如解图,连接BD交AC于点O,∵四边形ABCD是菱形,AB=5,AC=8,且菱形的对角线互相垂直平分,∴OA=4,在Rt△AOB中,由勾股定理得OB=3,∴BD=6,∴S菱形ABCD=AC·BD=×8×6=24.
解图
12. 【答案】110° 【解析】 ∵四边形ABCD是平行四边形,∴CD∥AB,∴∠CAB=∠1=20°,∵BE ⊥AB交对角线AC于点E,∴∠ABE=90°,∴∠2=∠CAB+∠ABE=20°+90°=110°.
13. 【答案】
【解析】如图,连结.
14. 【答案】
15. 【答案】16
【解析】∵ABCD的对角线AC、BD相交于点O,
∴BO=DO=BD,BD=2OB,∴O为BD中点,
∵点E是AB的中点,∴AB=2BE,BC=2OE,
∵四边形ABCD是平行四边形,∴AB=CD,∴CD=2BE.
∵△BEO的周长为8,∴OB+OE+BE=8,
∴BD+BC+CD=2OB+2OE+2BE=2(OB+OE+BE)=16,
∴△BCD的周长是16,故答案为16.
三、解答题
16. 【答案】
证明:(1)∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,∴∠BPA=∠DAE.
在△ABP和△DAE中,又∵∠ABC=∠AED,∴∠BAF=∠ADE.
∵∠ABF=∠BPF,∠BPA=∠DAE,
∴∠ABF=∠DAE,
又∵AB=DA,∴△ABF≌△DAE(ASA).
(2)∵△ABF≌△DAE,∴AE=BF,DE=AF.
∵AF=AE+EF=BF+EF,
∴DE=BF+EF.
17. 【答案】
证明:(1)在正六边形ABCDEF中,AB=AF=FE=ED=DC=BC=6,∠A=∠F=∠D=∠C=120°,
∵VP=VQ=1cm/s,∴AP=DQ=t,
∵PF=AF-AP=6-t,CQ=CD-DQ=6-t,
∴PF=CQ=6-t,
在△ABP和△DQE中,
AP=DQ=t,∠A =∠D =120°,AB=DE=6,
∴△ABP≌△DQE,∴BP=EQ,
同理可证△PEF≌△QBC,∴PE=QB,
∴四边形PBQE为平行四边形.
(2)连结BE,CO,DO,作CG⊥BE于点G,QH⊥BE于点H.
∵四边形PBQE是矩形,∴∠BQE=90°,
∴BE是正六边形ABCDEF的外接圆直径,
即BE过点O,且BE=12,
∵ED=DC=BC=6,
∴∠EOD=∠COD=∠BOC =60°,
又∵OE=OD=OC=OB,
∴△EOD,△COD,△BOC是全等的等边三角形,
∴CG=CO·sin∠BOC=CO·sin60°=6×=,
∴S△DOE= S△COD= S△BOC=BO·CG=×6×=,
∵∠BCD+∠CBO=180°,∴CD∥BE,
∵CG⊥BE,QH⊥BE,
∴QH=CG=,
∴S△BEQ=BE·QH=×12×=,
∵正六边形ABCDEF是以直线BE为对称轴的轴对称图形,矩形PBQE关于点O成中心对称,
∴===.
18. 【答案】
连结交于,∵四边形为矩形,∴,
∴,∴
∵平分,
∴,
∴
∵,
∴
∵,∴,
∴,
∴,
∴
