人教版 九年级数学 第25章 概率初步 课时训练(Word版含答案解析)
文档属性
| 名称 | 人教版 九年级数学 第25章 概率初步 课时训练(Word版含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 236.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 13:18:30 | ||
图片预览



文档简介
人教版 九年级数学 第25章 概率初步 课时训练
一、选择题
1. 同时抛掷三枚质地均匀的硬币,至少有两枚硬币正面向上的概率是( )
A. B. C. D.
2. 一个布袋里装有2个红球、3个黄球和5个白球,这些球除颜色不同外其他都相同.搅匀后任意摸出1个球,是白球的概率为( )
A. B. C. D.
3. 小李与小陈做猜拳游戏,规定每人每次至少出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么小李获胜的概率为( )
A. B. C. D.
4. 一个盒子中装有四张完全相同的卡片,上面分别写着2 cm,3 cm,4 cm和5 cm,盒子外有两张卡片,上面分别写着3 cm和5 cm,现随机从盒中取出一张卡片,与盒子外的两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,那么这三条线段能构成三角形的概率是( )
A. B. C. D.
5. 2019·毕节 在平行四边形ABCD中,AC,BD是两条对角线,现从以下四个关系:①AB=BC;②AC=BD;③AC⊥BD;④AB⊥BC中随机取出一个作为条件,能推出平行四边形ABCD是菱形的概率为( )
A. B. C. D.1
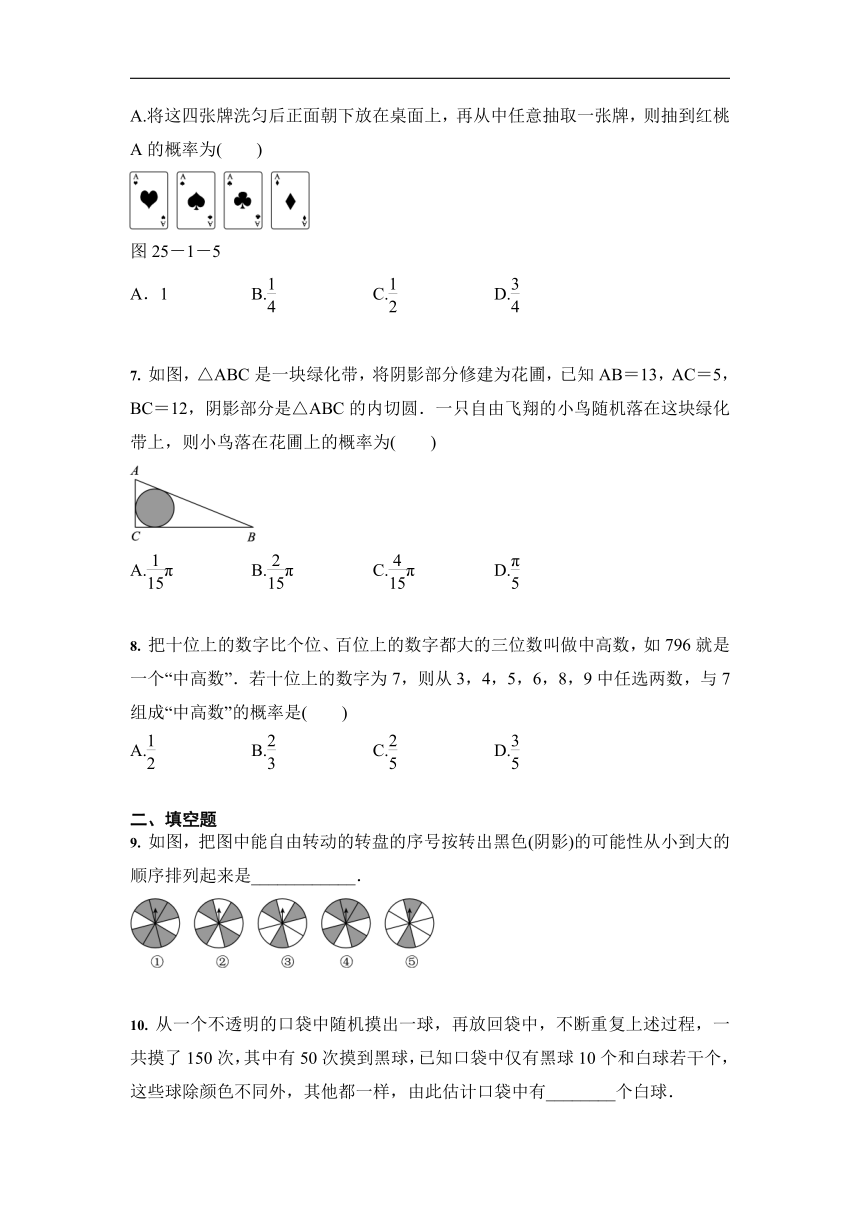
6. 2018·柳州 如图25-1-5,现有四张扑克牌:红桃A、黑桃A、梅花A和方块A.将这四张牌洗匀后正面朝下放在桌面上,再从中任意抽取一张牌,则抽到红桃A的概率为( )
图25-1-5
A.1 B. C. D.
7. 如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=13,AC=5,BC=12,阴影部分是△ABC的内切圆.一只自由飞翔的小鸟随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
A.π B.π C.π D.
8. 把十位上的数字比个位、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上的数字为7,则从3,4,5,6,8,9中任选两数,与7组成“中高数”的概率是( )
A. B. C. D.
二、填空题
9. 如图,把图中能自由转动的转盘的序号按转出黑色(阴影)的可能性从小到大的顺序排列起来是____________.
10. 从一个不透明的口袋中随机摸出一球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知口袋中仅有黑球10个和白球若干个,这些球除颜色不同外,其他都一样,由此估计口袋中有________个白球.
11. 掷一枚硬币三次,其中有两次正面朝上、一次反面朝上的概率为________.
12. 2019·贵阳 一个袋中装有m个红球,10个黄球,n个白球,每个球除颜色外都相同,任意摸出1个球,如果摸到黄球的概率与不是黄球的概率相同,那么m与n的关系是____________.
13. 一枚质地均匀的骰子,骰子的六个面上分别刻有1~6的点数.连续掷两次骰子,在骰子向上的一面上,第二次出现的点数是第一次出现的点数的2倍的概率是________.
14. 在-4,-2,1,2四个数中,随机取两个数分别作为函数y=ax2+bx+1中a,b的值,则该二次函数的图象恰好经过第一、二、四象限的概率为________.
15. 已知电路AB由如图所示的开关控制,闭合a,b,c,d,e五个开关中的任意两个,则能使电路形成通路的概率是________.
三、解答题
16. 甲、乙、丙三名同学站成一排合影留念.
(1)请按从左向右的顺序列出所有可能站位的结果;
(2)求出甲同学站在中间位置的概率.
17. 4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验.通过大量重复试验后发现,抽到合格品的频率稳定在0.95附近,则可以推算出x的值大约是多少?
18. 某校九年级学生共900人,为了解这个年级学生的体能,从中随机抽取部分学生进行1 min的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理.下面是这四名同学提供的部分信息:
甲:将全体测试数据分成6组绘成直方图(如图);
乙:跳绳次数不少于105次的同学占96%;
丙:第①、②两组频率之和为0.12,且第②组与第⑥组频数都是12;
丁:第②、③、④组的频数之比为4∶17∶15.
根据这四名同学提供的材料,请解答如下问题:
(1)这次跳绳测试共抽取多少名学生?各组有多少人?
(2)如果跳绳次数不少于135次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为多少?
(3)以每组的组中值(每组的中点对应的数据)作为这组跳绳次数的代表,估计这批学生1 min跳绳次数的平均值.
人教版 九年级数学 第25章 概率初步 课时训练-答案
一、选择题
1. 【答案】D [解析] 画树状图如下:
所以至少有两枚硬币正面向上的概率是=.
2. 【答案】A
3. 【答案】A [解析] 画树状图如下:
共有25种等可能的结果,两人出拳的手指数之和为偶数的结果有13种,所以小李获胜的概率为.故选A.
4. 【答案】D [解析] 共有四种等可能的结果,它们为2,3,5;3,3,5;4,3,5;5,3,5,其中三条线段能构成三角形的结果有3种,所以这三条线段能构成三角形的概率=.
5. 【答案】B
6. 【答案】B
7. 【答案】B [解析] 因为132=122+52,即AB2=BC2+AC2,所以△ABC为直角三角形,
所以△ABC的内切圆半径=×(12+5-13)=2.
所以S△ABC=AC·BC=×12×5=30,S圆=4π.
所以小鸟落在花圃上的概率===π.
故选B.
8. 【答案】C [解析] 列表如下:
由表格可知,所有等可能的结果有30种,其中组成“中高数”的结果有12种,因此组成“中高数”的概率为=.
二、填空题
9. 【答案】⑤③②④① [解析] 黑色部分多的转出黑色的可能性较大,故图中能自由转动的转盘的序号按转出黑色的可能性从小到大的顺序排列起来是⑤③②④①.
10. 【答案】20 [解析] 摸了150次,其中有50次摸到黑球,则摸到黑球的频率是=.
设口袋中有x个白球,则=,
解得x=20.
经检验,x=20是原方程的解,
故答案为20.
11. 【答案】 [解析] 画树状图如下:
∵共有8种等可能的结果,其中有两次正面朝上、一次反面朝上的结果有3种,
∴掷一枚硬币三次,其中有两次正面朝上、一次反面朝上的概率为.
12. 【答案】m+n=10 [解析] ∵一个袋中装有m个红球,10个黄球,n个白球,摸到黄球的概率与不是黄球的概率相同,∴m与n的关系是m+n=10.
故答案为m+n=10.
13. 【答案】 [解析] 因为本题两次抛掷结果互不影响,所以所有等可能出现的结果有6×6=36(种),其中第二次出现的点数是第一次出现的点数的2倍的结果有(1,2),(2,4),(3,6),共3种,所以根据概率计算公式,P==.故答案为.
14. 【答案】 [解析] 函数y=ax2+bx+1的图象一定经过y轴上的点(0,1),又知其图象经过第一、二、四象限,则图象的开口向上,对称轴在y轴的右侧,且与x轴正半轴有两个交点,所以a>0,b<0,b2-4ac>0.
列表如下:
由表可知,从-4,-2,1,2四个数中随机取两个数一共有12种等可能的结果,其中只有a=1,b=-4和a=2,b=-4这2种结果符合题意,所以所求概率==.
15. 【答案】 [解析] 列表如下:
∴一共有20种等可能的结果,使电路形成通路的结果有12种,
∴使电路形成通路的概率是=.
三、解答题
16. 【答案】
解:(1)三名同学的站法从左到右有(甲乙丙),(甲丙乙),(乙甲丙),(乙丙甲),(丙甲乙),(丙乙甲),共6种等可能的结果.
(2)甲同学站在中间位置的结果有2种,记为事件A,所以P(A)==.
17. 【答案】
解:(1)∵4件同型号的产品中,有1件不合格品,∴P(抽到的是不合格品)=.
(2)3件合格品分别用A,B,C表示,1件不合格品用a表示.可列出如下表格:
∵共有12种等可能的结果,其中抽到的都是合格品的结果有6种,
∴P(抽到的都是合格品)==.
(3)∵大量重复试验后发现,抽到合格品的频率稳定在0.95附近,
∴估计抽到合格品的概率为0.95,
∴=0.95,解得x=16.
经检验,x=16是原方程的根且符合题意.
∴x的值大约是16.
18. 【答案】
解:(1)第①组频率为1-96%=0.04.
∴第②组频率为0.12-0.04=0.08,
从而,总人数为12÷0.08=150人.
又②③④组的频数之比为4∶17∶15,可算得第①~⑥组的人数分别为6、12、51、45、24、12.
(2)第⑤、⑥两组的频率之和为0.16+0.08=0.24.由样本是随机抽取的,估计全年级有900×0.24=216人达到优秀.
(3)x=
=127(次).
一、选择题
1. 同时抛掷三枚质地均匀的硬币,至少有两枚硬币正面向上的概率是( )
A. B. C. D.
2. 一个布袋里装有2个红球、3个黄球和5个白球,这些球除颜色不同外其他都相同.搅匀后任意摸出1个球,是白球的概率为( )
A. B. C. D.
3. 小李与小陈做猜拳游戏,规定每人每次至少出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么小李获胜的概率为( )
A. B. C. D.
4. 一个盒子中装有四张完全相同的卡片,上面分别写着2 cm,3 cm,4 cm和5 cm,盒子外有两张卡片,上面分别写着3 cm和5 cm,现随机从盒中取出一张卡片,与盒子外的两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,那么这三条线段能构成三角形的概率是( )
A. B. C. D.
5. 2019·毕节 在平行四边形ABCD中,AC,BD是两条对角线,现从以下四个关系:①AB=BC;②AC=BD;③AC⊥BD;④AB⊥BC中随机取出一个作为条件,能推出平行四边形ABCD是菱形的概率为( )
A. B. C. D.1
6. 2018·柳州 如图25-1-5,现有四张扑克牌:红桃A、黑桃A、梅花A和方块A.将这四张牌洗匀后正面朝下放在桌面上,再从中任意抽取一张牌,则抽到红桃A的概率为( )
图25-1-5
A.1 B. C. D.
7. 如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=13,AC=5,BC=12,阴影部分是△ABC的内切圆.一只自由飞翔的小鸟随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
A.π B.π C.π D.
8. 把十位上的数字比个位、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上的数字为7,则从3,4,5,6,8,9中任选两数,与7组成“中高数”的概率是( )
A. B. C. D.
二、填空题
9. 如图,把图中能自由转动的转盘的序号按转出黑色(阴影)的可能性从小到大的顺序排列起来是____________.
10. 从一个不透明的口袋中随机摸出一球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知口袋中仅有黑球10个和白球若干个,这些球除颜色不同外,其他都一样,由此估计口袋中有________个白球.
11. 掷一枚硬币三次,其中有两次正面朝上、一次反面朝上的概率为________.
12. 2019·贵阳 一个袋中装有m个红球,10个黄球,n个白球,每个球除颜色外都相同,任意摸出1个球,如果摸到黄球的概率与不是黄球的概率相同,那么m与n的关系是____________.
13. 一枚质地均匀的骰子,骰子的六个面上分别刻有1~6的点数.连续掷两次骰子,在骰子向上的一面上,第二次出现的点数是第一次出现的点数的2倍的概率是________.
14. 在-4,-2,1,2四个数中,随机取两个数分别作为函数y=ax2+bx+1中a,b的值,则该二次函数的图象恰好经过第一、二、四象限的概率为________.
15. 已知电路AB由如图所示的开关控制,闭合a,b,c,d,e五个开关中的任意两个,则能使电路形成通路的概率是________.
三、解答题
16. 甲、乙、丙三名同学站成一排合影留念.
(1)请按从左向右的顺序列出所有可能站位的结果;
(2)求出甲同学站在中间位置的概率.
17. 4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验.通过大量重复试验后发现,抽到合格品的频率稳定在0.95附近,则可以推算出x的值大约是多少?
18. 某校九年级学生共900人,为了解这个年级学生的体能,从中随机抽取部分学生进行1 min的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理.下面是这四名同学提供的部分信息:
甲:将全体测试数据分成6组绘成直方图(如图);
乙:跳绳次数不少于105次的同学占96%;
丙:第①、②两组频率之和为0.12,且第②组与第⑥组频数都是12;
丁:第②、③、④组的频数之比为4∶17∶15.
根据这四名同学提供的材料,请解答如下问题:
(1)这次跳绳测试共抽取多少名学生?各组有多少人?
(2)如果跳绳次数不少于135次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为多少?
(3)以每组的组中值(每组的中点对应的数据)作为这组跳绳次数的代表,估计这批学生1 min跳绳次数的平均值.
人教版 九年级数学 第25章 概率初步 课时训练-答案
一、选择题
1. 【答案】D [解析] 画树状图如下:
所以至少有两枚硬币正面向上的概率是=.
2. 【答案】A
3. 【答案】A [解析] 画树状图如下:
共有25种等可能的结果,两人出拳的手指数之和为偶数的结果有13种,所以小李获胜的概率为.故选A.
4. 【答案】D [解析] 共有四种等可能的结果,它们为2,3,5;3,3,5;4,3,5;5,3,5,其中三条线段能构成三角形的结果有3种,所以这三条线段能构成三角形的概率=.
5. 【答案】B
6. 【答案】B
7. 【答案】B [解析] 因为132=122+52,即AB2=BC2+AC2,所以△ABC为直角三角形,
所以△ABC的内切圆半径=×(12+5-13)=2.
所以S△ABC=AC·BC=×12×5=30,S圆=4π.
所以小鸟落在花圃上的概率===π.
故选B.
8. 【答案】C [解析] 列表如下:
由表格可知,所有等可能的结果有30种,其中组成“中高数”的结果有12种,因此组成“中高数”的概率为=.
二、填空题
9. 【答案】⑤③②④① [解析] 黑色部分多的转出黑色的可能性较大,故图中能自由转动的转盘的序号按转出黑色的可能性从小到大的顺序排列起来是⑤③②④①.
10. 【答案】20 [解析] 摸了150次,其中有50次摸到黑球,则摸到黑球的频率是=.
设口袋中有x个白球,则=,
解得x=20.
经检验,x=20是原方程的解,
故答案为20.
11. 【答案】 [解析] 画树状图如下:
∵共有8种等可能的结果,其中有两次正面朝上、一次反面朝上的结果有3种,
∴掷一枚硬币三次,其中有两次正面朝上、一次反面朝上的概率为.
12. 【答案】m+n=10 [解析] ∵一个袋中装有m个红球,10个黄球,n个白球,摸到黄球的概率与不是黄球的概率相同,∴m与n的关系是m+n=10.
故答案为m+n=10.
13. 【答案】 [解析] 因为本题两次抛掷结果互不影响,所以所有等可能出现的结果有6×6=36(种),其中第二次出现的点数是第一次出现的点数的2倍的结果有(1,2),(2,4),(3,6),共3种,所以根据概率计算公式,P==.故答案为.
14. 【答案】 [解析] 函数y=ax2+bx+1的图象一定经过y轴上的点(0,1),又知其图象经过第一、二、四象限,则图象的开口向上,对称轴在y轴的右侧,且与x轴正半轴有两个交点,所以a>0,b<0,b2-4ac>0.
列表如下:
由表可知,从-4,-2,1,2四个数中随机取两个数一共有12种等可能的结果,其中只有a=1,b=-4和a=2,b=-4这2种结果符合题意,所以所求概率==.
15. 【答案】 [解析] 列表如下:
∴一共有20种等可能的结果,使电路形成通路的结果有12种,
∴使电路形成通路的概率是=.
三、解答题
16. 【答案】
解:(1)三名同学的站法从左到右有(甲乙丙),(甲丙乙),(乙甲丙),(乙丙甲),(丙甲乙),(丙乙甲),共6种等可能的结果.
(2)甲同学站在中间位置的结果有2种,记为事件A,所以P(A)==.
17. 【答案】
解:(1)∵4件同型号的产品中,有1件不合格品,∴P(抽到的是不合格品)=.
(2)3件合格品分别用A,B,C表示,1件不合格品用a表示.可列出如下表格:
∵共有12种等可能的结果,其中抽到的都是合格品的结果有6种,
∴P(抽到的都是合格品)==.
(3)∵大量重复试验后发现,抽到合格品的频率稳定在0.95附近,
∴估计抽到合格品的概率为0.95,
∴=0.95,解得x=16.
经检验,x=16是原方程的根且符合题意.
∴x的值大约是16.
18. 【答案】
解:(1)第①组频率为1-96%=0.04.
∴第②组频率为0.12-0.04=0.08,
从而,总人数为12÷0.08=150人.
又②③④组的频数之比为4∶17∶15,可算得第①~⑥组的人数分别为6、12、51、45、24、12.
(2)第⑤、⑥两组的频率之和为0.16+0.08=0.24.由样本是随机抽取的,估计全年级有900×0.24=216人达到优秀.
(3)x=
=127(次).
同课章节目录
