人教版七年级数学下学期:5.3 《平行线的性质》 同步练习(word版,含答案)
文档属性
| 名称 | 人教版七年级数学下学期:5.3 《平行线的性质》 同步练习(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 52.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 20:28:35 | ||
图片预览


文档简介
5.3
平行线的性质
一.选择题
1.下列语句是命题的是( )
A.画直线AB
B.直线a∥b
C.如果a∥b,b∥c,则a∥c
D.点M与点N都在直线AB上
2.下列命题中,真命题的个数是( )
①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③图形平移的方向一定是水平的;④内错角相等;⑤相等的角是对顶角;⑥垂线段最短
A.3
B.2
C.1
D.0
3.下列五个命题:
①如果两个数的绝对值相等,那么这两个数的平方相等;
②内错角相等;
③在同一平面内,垂直于同一条直线的两条直线互相平行;
④两个无理数的和一定是无理数;
⑤坐标平面内的点与有序数对是一一对应的.
其中真命题的个数是( )
A.2个
B.3个
C.4个
D.5个
4.下列选项中a,b的取值,可以说明“若a>b,则|a|>|b|”是假命题的反例为( )
A.a=﹣5
b=﹣6
B.a=6
b=5
C.a=﹣6
b=5
D.a=6
b=﹣5
5.下列命题中,逆命题为真命题的是( )
A.对顶角相等
B.邻补角互补
C.两直线平行,同位角相等
D.互余的两个角都小于90°
6.如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为( )
A.80°
B.90°
C.100°
D.102°
7.如图,直线a,b被直线m所截,若a∥b,∠2=62°,则∠1=( )
A.62°
B.108°
C.118°
D.128°
8.能说明“锐角α,锐角β的和是锐角”是假命题的例证图是( )
A.
B.
C.
D.
9.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A.30°
B.40°
C.50°
D.60°
10.若直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a,b间的距离是( )cm.
A.2
B.8
C.2或8
D.4
二.填空题
11.若a2=b2,那么a=b;请举出一个反例,说明该命题是假命题;
12.把命题“两直线平行,同位角相等”改写成“如果…那么…”的形式是:
.
13.“同角的余角相等”,这个命题改写成如果…那么…形式应该为
.
三.解答题
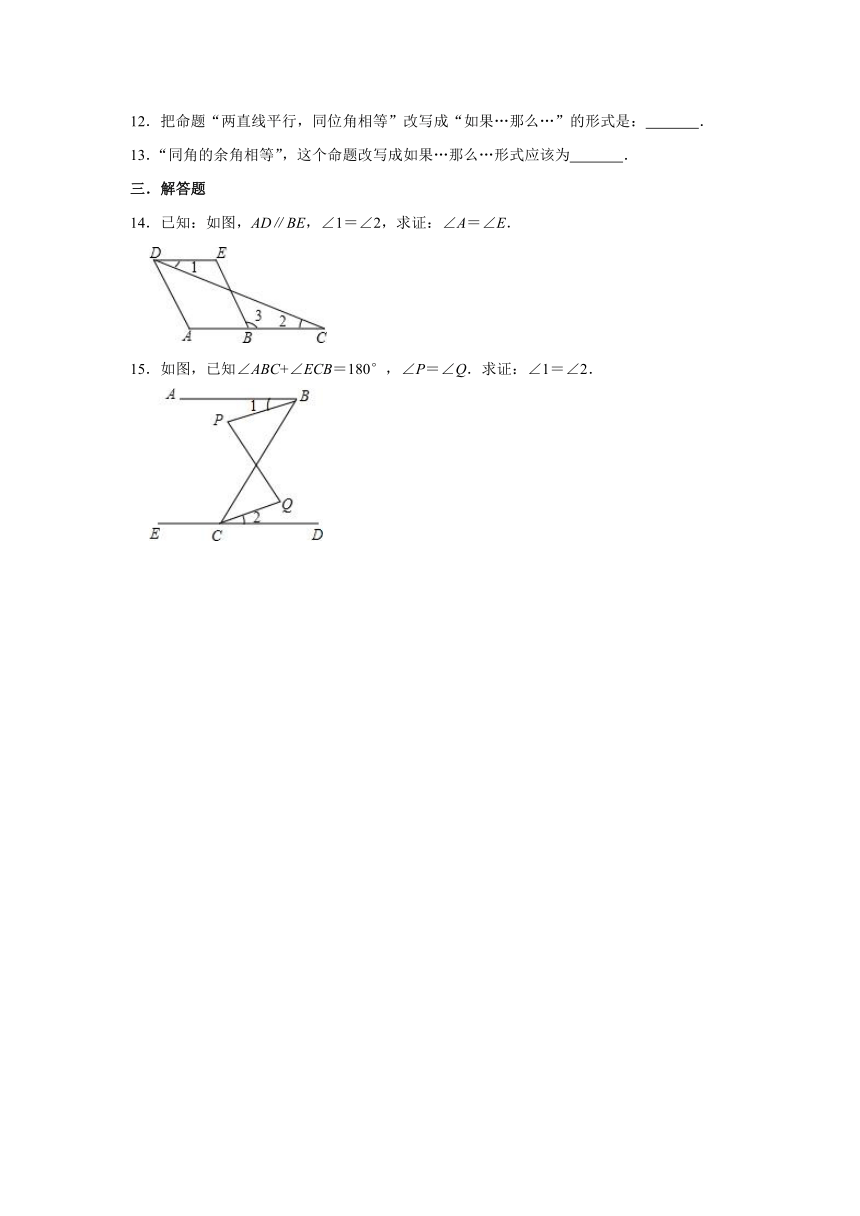
14.已知:如图,AD∥BE,∠1=∠2,求证:∠A=∠E.
15.如图,已知∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
参考答案
一.选择题
1.解:C是用数学式子表达的可以判断真假的陈述句,是命题;
A、B、D均不是可以判断真假的陈述句,没有题设和结论之分,都不是命题.
故选:C.
2.解:过直线外一点有且只有一条直线与已知直线平行,①是假命题;
在同一平面内,过一点有且只有一条直线与已知直线垂直,②是假命题;
图形平移的方向不一定是水平的,③是假命题;
两直线平行,内错角相等,④是假命题;
相等的角不一定是对顶角,⑤是假命题;
垂线段最短,⑥是真命题,
故选:C.
3.解:①如果两个数的绝对值相等,那么这两个数的平方相等,是真命题;
②两直线平行,内错角相等,原命题是假命题;
③在同一平面内,垂直于同一条直线的两条直线互相平行,是真命题;
④两个无理数的和不一定是无理数,原命题是假命题;
⑤坐标平面内的点与有序数对是一一对应的,是真命题;
故选:B.
4.解:当a=﹣5,b=﹣6时,a>b,但|a|<|b|,
∴“若a>b,则|a|>|b|”是假命题,
故选:A.
5.解:A、对顶角相等的逆命题是相等的角是对顶角,逆命题是假命题;
B、邻补角互补的逆命题是互补的角是邻补角,逆命题是假命题;
C、两直线平行,同位角相等逆命题是同位角相等,两直线平行,逆命题是真命题;
D、互余的两个角都小于90°的逆命题是都小于90°的角互余,逆命题是假命题;
故选:C.
6.解:∵AB∥CD,
∴∠A=∠3=40°,
∵∠1=120°,
∴∠2=∠1﹣∠A=80°,
故选:A.
7.解:
如图,∵a∥b,
∴∠3=∠2=62°,
∵∠3+∠1=180°,
∴∠1=180°﹣62°=118°.
故选:C.
8.解:例如C选项图中:三角形三个内角都是锐角,则∠α+∠β>90°.
故选:C.
9.解:如图,∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,
∴∠BEF=∠1+∠F=50°,
∵AB∥CD,
∴∠2=∠BEF=50°,
故选:C.
10.解:分为两种情况:
如图1,直线a,b间的距离是5cm﹣3cm=2cm,
如图2,直线a,b间的距离是5cm+3cm=8cm,
故选:C.
二.填空题
11.解:若a2=b2,那么a=b,是假命题.
例如:22=(﹣2)2=4
但是2≠﹣2.
所以答案可以是:若22=(﹣2)2=4,但是2≠﹣2.
12.解:“两直线平行,同位角相等”的条件是:“两直线平行”,结论为:“同位角相等”,
∴写成“如果…,那么…”的形式为:“如果两直线平行,那么同位角相等”,
故答案为:如果两直线平行,那么同位角相等.
13.解:根据命题的特点,可以改写为:“如果两个角是同一个角的余角,那么这两个角相等”,
故答案为:如果两个角是同一个角的余角,那么这两个角相等.
三.解答题
14.证明:∵AD∥BE,
∴∠A=∠3,
∵∠1=∠2,
∴DE∥AC,
∴∠E=∠3,
∴∠A=∠EBC=∠E.
15.证明:∵∠ABC+∠ECB=180°,
∴AB∥DE,
∴∠ABC=∠BCD,
∵∠P=∠Q,
∴PB∥CQ,
∴∠PBC=∠BCQ,
∵∠1=∠ABC﹣∠PBC,∠2=∠BCD﹣∠BCQ,
∴∠1=∠2.
平行线的性质
一.选择题
1.下列语句是命题的是( )
A.画直线AB
B.直线a∥b
C.如果a∥b,b∥c,则a∥c
D.点M与点N都在直线AB上
2.下列命题中,真命题的个数是( )
①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③图形平移的方向一定是水平的;④内错角相等;⑤相等的角是对顶角;⑥垂线段最短
A.3
B.2
C.1
D.0
3.下列五个命题:
①如果两个数的绝对值相等,那么这两个数的平方相等;
②内错角相等;
③在同一平面内,垂直于同一条直线的两条直线互相平行;
④两个无理数的和一定是无理数;
⑤坐标平面内的点与有序数对是一一对应的.
其中真命题的个数是( )
A.2个
B.3个
C.4个
D.5个
4.下列选项中a,b的取值,可以说明“若a>b,则|a|>|b|”是假命题的反例为( )
A.a=﹣5
b=﹣6
B.a=6
b=5
C.a=﹣6
b=5
D.a=6
b=﹣5
5.下列命题中,逆命题为真命题的是( )
A.对顶角相等
B.邻补角互补
C.两直线平行,同位角相等
D.互余的两个角都小于90°
6.如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为( )
A.80°
B.90°
C.100°
D.102°
7.如图,直线a,b被直线m所截,若a∥b,∠2=62°,则∠1=( )
A.62°
B.108°
C.118°
D.128°
8.能说明“锐角α,锐角β的和是锐角”是假命题的例证图是( )
A.
B.
C.
D.
9.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A.30°
B.40°
C.50°
D.60°
10.若直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a,b间的距离是( )cm.
A.2
B.8
C.2或8
D.4
二.填空题
11.若a2=b2,那么a=b;请举出一个反例,说明该命题是假命题;
12.把命题“两直线平行,同位角相等”改写成“如果…那么…”的形式是:
.
13.“同角的余角相等”,这个命题改写成如果…那么…形式应该为
.
三.解答题
14.已知:如图,AD∥BE,∠1=∠2,求证:∠A=∠E.
15.如图,已知∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
参考答案
一.选择题
1.解:C是用数学式子表达的可以判断真假的陈述句,是命题;
A、B、D均不是可以判断真假的陈述句,没有题设和结论之分,都不是命题.
故选:C.
2.解:过直线外一点有且只有一条直线与已知直线平行,①是假命题;
在同一平面内,过一点有且只有一条直线与已知直线垂直,②是假命题;
图形平移的方向不一定是水平的,③是假命题;
两直线平行,内错角相等,④是假命题;
相等的角不一定是对顶角,⑤是假命题;
垂线段最短,⑥是真命题,
故选:C.
3.解:①如果两个数的绝对值相等,那么这两个数的平方相等,是真命题;
②两直线平行,内错角相等,原命题是假命题;
③在同一平面内,垂直于同一条直线的两条直线互相平行,是真命题;
④两个无理数的和不一定是无理数,原命题是假命题;
⑤坐标平面内的点与有序数对是一一对应的,是真命题;
故选:B.
4.解:当a=﹣5,b=﹣6时,a>b,但|a|<|b|,
∴“若a>b,则|a|>|b|”是假命题,
故选:A.
5.解:A、对顶角相等的逆命题是相等的角是对顶角,逆命题是假命题;
B、邻补角互补的逆命题是互补的角是邻补角,逆命题是假命题;
C、两直线平行,同位角相等逆命题是同位角相等,两直线平行,逆命题是真命题;
D、互余的两个角都小于90°的逆命题是都小于90°的角互余,逆命题是假命题;
故选:C.
6.解:∵AB∥CD,
∴∠A=∠3=40°,
∵∠1=120°,
∴∠2=∠1﹣∠A=80°,
故选:A.
7.解:
如图,∵a∥b,
∴∠3=∠2=62°,
∵∠3+∠1=180°,
∴∠1=180°﹣62°=118°.
故选:C.
8.解:例如C选项图中:三角形三个内角都是锐角,则∠α+∠β>90°.
故选:C.
9.解:如图,∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,
∴∠BEF=∠1+∠F=50°,
∵AB∥CD,
∴∠2=∠BEF=50°,
故选:C.
10.解:分为两种情况:
如图1,直线a,b间的距离是5cm﹣3cm=2cm,
如图2,直线a,b间的距离是5cm+3cm=8cm,
故选:C.
二.填空题
11.解:若a2=b2,那么a=b,是假命题.
例如:22=(﹣2)2=4
但是2≠﹣2.
所以答案可以是:若22=(﹣2)2=4,但是2≠﹣2.
12.解:“两直线平行,同位角相等”的条件是:“两直线平行”,结论为:“同位角相等”,
∴写成“如果…,那么…”的形式为:“如果两直线平行,那么同位角相等”,
故答案为:如果两直线平行,那么同位角相等.
13.解:根据命题的特点,可以改写为:“如果两个角是同一个角的余角,那么这两个角相等”,
故答案为:如果两个角是同一个角的余角,那么这两个角相等.
三.解答题
14.证明:∵AD∥BE,
∴∠A=∠3,
∵∠1=∠2,
∴DE∥AC,
∴∠E=∠3,
∴∠A=∠EBC=∠E.
15.证明:∵∠ABC+∠ECB=180°,
∴AB∥DE,
∴∠ABC=∠BCD,
∵∠P=∠Q,
∴PB∥CQ,
∴∠PBC=∠BCQ,
∵∠1=∠ABC﹣∠PBC,∠2=∠BCD﹣∠BCQ,
∴∠1=∠2.
