北师大版数学九年级下第三章《圆》高分突破压轴专练(一)(Word版含答案解析)
文档属性
| 名称 | 北师大版数学九年级下第三章《圆》高分突破压轴专练(一)(Word版含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 233.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 13:48:42 | ||
图片预览




文档简介
第三章《圆》高分突破压轴专练(一)
1.如图,以AC为直径的⊙O与△ABC的AB、BC两边分别交于D、E两点,AB=AC,EF⊥AB,垂足为F,延长FE与AC交于点G.
(1)求证:EF是⊙O的切线;
(2)若AC=2CE,则cosG为
.
2.如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F.切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,若AC∥EF,试判断线段KG、KD、GE间的数量关系,并说明理由;
(3)在(2)的条件下,若sinE=,AK=2,求⊙O的半径.
3.如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP.
4.如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D.
(1)判断BC、MD的位置关系,并说明理由;
(2)若AE=16,BE=4,求线段CD的长.
5.如图,⊙O过?ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AP交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=,求⊙O的半径.
6.如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)已知AE=8cm,CD=12cm,求⊙O的半径.
7.已知AM是⊙O直径,弦BC⊥AM,垂足为点N,弦CD交AM于点E,连接AB和BE.
(1)如图1,若CD⊥AB,垂足为点F,求证:∠BED=2∠BAM;
(2)如图2,在(1)的条件下,连接BD,若∠ABE=∠BDC,求证:AE=2CN;
(3)如图3,AB=CD,BE:CD=4:7,AE=11,求EM的长.
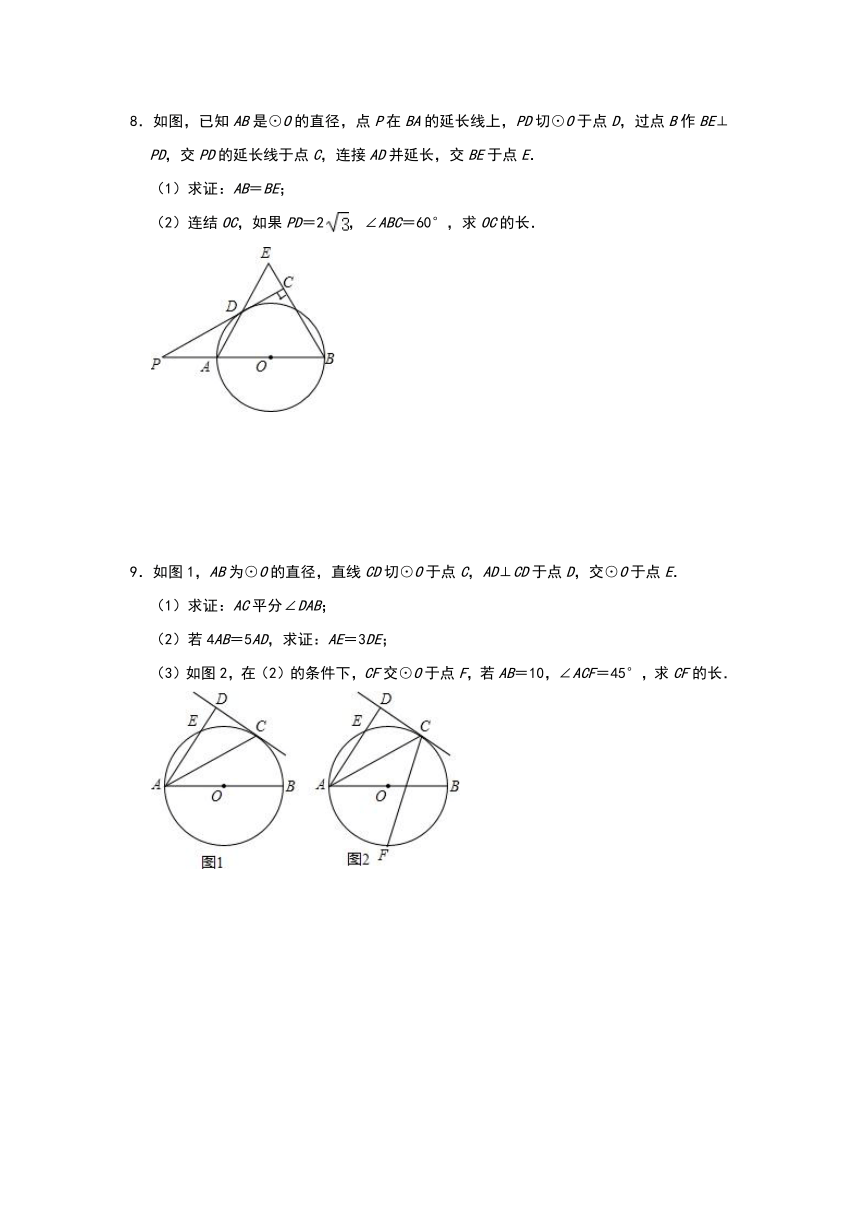
8.如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE⊥PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)连结OC,如果PD=2,∠ABC=60°,求OC的长.
9.如图1,AB为⊙O的直径,直线CD切⊙O于点C,AD⊥CD于点D,交⊙O于点E.
(1)求证:AC平分∠DAB;
(2)若4AB=5AD,求证:AE=3DE;
(3)如图2,在(2)的条件下,CF交⊙O于点F,若AB=10,∠ACF=45°,求CF的长.
10.如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO.
(1)求证:△ABD∽△OBC;
(2)若AB=2,BC=,求AD的长.
参考答案
1.证明:(1)如图,连接OE.
∵AB=AC,
∴∠B=∠ACB.
在⊙O中,OC=OE,
∴∠OEC=∠ACB.
∴∠B=∠OEC.
∴OE∥AB.
又
AB⊥GF,
∴OE⊥GF.
又
OE是⊙O的半径,
∴FG与⊙O相切.
解:(2)如图,连接AE,
∵AC是⊙O的直径,
∵∠AEC=90°,
∴AE⊥BC,
∵AB=AC,
∴CE=BE=BC,
∵AC=2CE,
∴AC=BC=AB,
∴△ABC是等边三角形,
∴∠ACB=60°,
∴∠COE=60°,
∵∠OEC=90°,
∴∠G=30°,
∴cosG=cos30°=.
故答案为:.
2.解:(1)如图1,连接OG.
∵EG为切线,
∴∠KGE+∠OGA=90°,
∵CD⊥AB,
∴∠AKH+∠OAG=90°,
又∵OA=OG,
∴∠OGA=∠OAG,
∴∠KGE=∠AKH=∠GKE,
∴KE=GE.
(2)KG2=KD?GE,理由是:
连接GD,如图2,
∵AC∥EF,
∴∠C=∠E,
∵∠C=∠AGD,
∴∠E=∠AGD,
∵∠GKD=∠GKD,
∴△GKD∽△EKG,
∴,
∴KG2=KD?EK,
由(1)得:EK=GE,
∴KG2=KD?GE;
(3)连接OG,OC,如图3所示,
由(1)得:KE=GE.
∵AC∥EF
∴∠E=∠ACH
∵sinE=sin∠ACH=,
设AH=3t,则AC=5t,CH=4t,
∵KE=GE,AC∥EF,
∴CK=AC=5t,
∴HK=CK﹣CH=t.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即(3t)2+t2=,解得t=.
设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3t,CH=4t,
由勾股定理得:OH2+CH2=OC2,
即(r﹣3t)2+(4t)2=r2,解得r=t=,
答:⊙O的半径为.
3.证明:(1)连接OE,如图,
∵CD为直径,
∴∠CED=90°,即∠CEO+∠OED=90°,
∵OC=OE,
∴∠C=∠CEO,
∴∠C+∠OED=90°,
∵∠PED=∠C.
∴∠PED+∠OED=90°,即∠OEP=90°,
∴OE⊥PE,
∴PE是⊙O的切线;
(2)∵AB为直径,
∴∠AEB=90°,
而AE∥CD,
∴∠EFD=90°,
∴∠FED+∠EDF=90°,
而∠C+∠EDC=90°,
∴∠FED=∠C,
∴∠PED=∠FED,
∴ED平分∠BEP.
4.解:(1)BC、MD的位置关系是平行,
理由:∵∠M=∠D,
∴,
∴∠M=∠MBC,
∴BC∥MD;
(2)连接OC,
∵AB是⊙O的直径,弦CD⊥AB于点E,AE=16,BE=4,
∴∠OEC=90°,EC=ED,AB=AE+BE=20,
∴OC=10,OE=OB﹣BE=6,
∴CE=,
∴CD=2CE=16,
即线段CD的长是16.
5.(1)证明:∵四边形ADCH是圆内接四边形,
∴∠ADC+∠AHC=180°,
又∵∠AHC+∠AHB=180°,
∴∠ADC=∠AHB,
∵四边形ABCD是平行四边形,
∴∠ADC=∠B,
∴∠AHB=∠B,
∴AB=AH,
∴△ABH是等腰三角形;
(2)证明:连接OC,如右图所示,
∵边AB与⊙O相切于点A,
∴BA⊥AF,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴CD⊥AF,
又∵FA经过圆心O,
∴,∠OEC=90°,
∴∠COF=2∠DAF,
又∵∠PCD=2∠DAF,
∴∠COF=∠PCD,
∵∠COF+∠OCE=90°,
∴∠PCD+∠OCE=90°,
即∠OCP=90°,
∴直线PC是⊙O的切线;
(3)∵四边形ABCD是平行四边形,
∴DC=AB=2,
∵FA⊥CD,
∴DE=CE=1,
∵∠AED=90°,AD=,DE=1,
∴AE=,
设⊙O的半径为r,则OA=OD=r,OE=AE﹣OA=4﹣r,
∵∠OED=90°,DE=1,
∴r2=(4﹣r)2+12
解得,r=,
即⊙O的半径是.
6.(1)证明:连结OA.
∵OA=OD,
∴∠ODA=∠OAD.
∵DA平分∠BDE,
∴∠ODA=∠EDA.
∴∠OAD=∠EDA,
∴EC∥OA.
∵AE⊥CD,
∴OA⊥AE.
∵点A在⊙O上,
∴AE是⊙O的切线.
(2)解:过点O作OF⊥CD,垂足为点F.
∵∠OAE=∠AED=∠OFD=90°,
∴四边形AOFE是矩形.
∴OF=AE=8cm.
又∵OF⊥CD,
∴DF=CD=6cm.
在Rt△ODF中,OD==10cm,
即⊙O的半径为10cm.
7.解:(1)∵BC⊥AM,CD⊥AB,
∴∠ENC=∠EFA=90°.
∵∠AEF=∠CEN,
∴∠BAM=∠BCD.
∵AM是⊙O直径,弦BC⊥AM,
∴BN=CN,
∴EB=EC,
∴∠EBC=∠BCD,
∴∠BED=2∠BCD=2∠BAM;
(2)连接AC,如图2,
∵AM是⊙O直径,弦BC⊥AM,
∴=,
∴∠BAM=∠CAM,
∴∠BDC=∠BAC=2∠BAM=∠BED,
∴BD=BE.
在△ABE和△CDB中,
,
∴△ABE≌△CDB,
∴AE=CB.
∵BN=CN,
∴AE=CB=2CN;
(3)过点O作OP⊥AB于P,作OH⊥BE于H,作OQ⊥CD于Q,连接OC,如图3,
则有AP=BP=AB,CQ=DQ=CD.
∵AB=CD,
∴AP=CQ,
∴OP===OQ.
∵AM垂直平分BC,
∴EB=EC,
∴∠BEA=∠CEA.
∵OH⊥BE,OQ⊥CD,
∴OH=OQ,
∴OP=OQ=OH,
∴====.
又∵=,
∴=.
设AO=7k,则EO=4k,
∴AE=AO+EO=11k=11,
∴k=1,
∴AO=7,EO=4,
∴AM=2AO=14,
∴EM=AM﹣AE=14﹣11=3.
8.(1)证明:连接OD,
∵PD切⊙O于点D,
∴OD⊥PD,
∵BE⊥PC,
∴OD∥BE,
∴ADO=∠E,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠E,
∴AB=BE;
(2)解:∵OD∥BE,∠ABC=60°,
∴∠DOP=∠ABC=60°,
∵PD⊥OD,
∴tan∠DOP=,
∴,
∴OD=2,
∴OP=4,
∴PB=6,
∴sin∠ABC=,
∴,
∴PC=3,
∴DC=,
∴DC2+OD2=OC2,
∴()2+22=OC2,
∴OC=.
9.解:(1)连接OC,如图1①,
∵CD为⊙O的切线,
∴OC⊥CD.
∵AD⊥CD,
∴OC∥AD,
∴∠CAD=∠ACO.
又∵OC=OA,
∴∠ACO=∠OAC,
∴∠CAD=∠OAC,
∴AC平分∠DAB;
(2)连接BC、EC、OC,如图1②,
设AB=5x,则由4AB=5AD可得AD=4x.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ADC=∠ACB=90°.
∵∠DAC=∠CAB,
∴△ADC∽△ACB,
∴=,
∴AC2=AD?AB=20x2,
∴DC2=AC2﹣AD2=20x2﹣16x2=4x2.
∵直线CD与⊙O相切,
∴根据切割线定理可得CD2=DE?DA,
∴4x2=DE?4x,
∴DE=x,
∴AE=3x=3DE;
(3)过点A作AH⊥FC,连接AF,如图2,
∵AB=5x=10,
∴OA=OF=5,x=2,
∴AC2=20x2=80,
∴AC=4.
∵∠ACF=45°,
∴AH=AC?sin∠ACH=4×=2,
CH=AC?cos∠ACH=4×=2.
∵∠AOF=2∠ACF=90°,
∴AF==5,
∴FH==,
∴FC=CH+FH=3,
即CF的长为3.
10.(1)证明:∵AB是⊙O的直径,
∴∠ADB=∠90°,
∵BC是⊙O的切线,
∴∠OBC=∠90°,
∵AD∥CO,
∴∠A=∠COB,
在△ABD和△OBC中
∵∠ADB=∠OBC,∠A=∠COB,
∴△ABD∽△OCB;
(2)由(1)知,△ABD∽△OCB,
∴=,即AD=,
∵AB=2,BC=,
∴OB=1,
∴OC==,
∴AD==.
1.如图,以AC为直径的⊙O与△ABC的AB、BC两边分别交于D、E两点,AB=AC,EF⊥AB,垂足为F,延长FE与AC交于点G.
(1)求证:EF是⊙O的切线;
(2)若AC=2CE,则cosG为
.
2.如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F.切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,若AC∥EF,试判断线段KG、KD、GE间的数量关系,并说明理由;
(3)在(2)的条件下,若sinE=,AK=2,求⊙O的半径.
3.如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP.
4.如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D.
(1)判断BC、MD的位置关系,并说明理由;
(2)若AE=16,BE=4,求线段CD的长.
5.如图,⊙O过?ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AP交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=,求⊙O的半径.
6.如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)已知AE=8cm,CD=12cm,求⊙O的半径.
7.已知AM是⊙O直径,弦BC⊥AM,垂足为点N,弦CD交AM于点E,连接AB和BE.
(1)如图1,若CD⊥AB,垂足为点F,求证:∠BED=2∠BAM;
(2)如图2,在(1)的条件下,连接BD,若∠ABE=∠BDC,求证:AE=2CN;
(3)如图3,AB=CD,BE:CD=4:7,AE=11,求EM的长.
8.如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE⊥PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)连结OC,如果PD=2,∠ABC=60°,求OC的长.
9.如图1,AB为⊙O的直径,直线CD切⊙O于点C,AD⊥CD于点D,交⊙O于点E.
(1)求证:AC平分∠DAB;
(2)若4AB=5AD,求证:AE=3DE;
(3)如图2,在(2)的条件下,CF交⊙O于点F,若AB=10,∠ACF=45°,求CF的长.
10.如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO.
(1)求证:△ABD∽△OBC;
(2)若AB=2,BC=,求AD的长.
参考答案
1.证明:(1)如图,连接OE.
∵AB=AC,
∴∠B=∠ACB.
在⊙O中,OC=OE,
∴∠OEC=∠ACB.
∴∠B=∠OEC.
∴OE∥AB.
又
AB⊥GF,
∴OE⊥GF.
又
OE是⊙O的半径,
∴FG与⊙O相切.
解:(2)如图,连接AE,
∵AC是⊙O的直径,
∵∠AEC=90°,
∴AE⊥BC,
∵AB=AC,
∴CE=BE=BC,
∵AC=2CE,
∴AC=BC=AB,
∴△ABC是等边三角形,
∴∠ACB=60°,
∴∠COE=60°,
∵∠OEC=90°,
∴∠G=30°,
∴cosG=cos30°=.
故答案为:.
2.解:(1)如图1,连接OG.
∵EG为切线,
∴∠KGE+∠OGA=90°,
∵CD⊥AB,
∴∠AKH+∠OAG=90°,
又∵OA=OG,
∴∠OGA=∠OAG,
∴∠KGE=∠AKH=∠GKE,
∴KE=GE.
(2)KG2=KD?GE,理由是:
连接GD,如图2,
∵AC∥EF,
∴∠C=∠E,
∵∠C=∠AGD,
∴∠E=∠AGD,
∵∠GKD=∠GKD,
∴△GKD∽△EKG,
∴,
∴KG2=KD?EK,
由(1)得:EK=GE,
∴KG2=KD?GE;
(3)连接OG,OC,如图3所示,
由(1)得:KE=GE.
∵AC∥EF
∴∠E=∠ACH
∵sinE=sin∠ACH=,
设AH=3t,则AC=5t,CH=4t,
∵KE=GE,AC∥EF,
∴CK=AC=5t,
∴HK=CK﹣CH=t.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即(3t)2+t2=,解得t=.
设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3t,CH=4t,
由勾股定理得:OH2+CH2=OC2,
即(r﹣3t)2+(4t)2=r2,解得r=t=,
答:⊙O的半径为.
3.证明:(1)连接OE,如图,
∵CD为直径,
∴∠CED=90°,即∠CEO+∠OED=90°,
∵OC=OE,
∴∠C=∠CEO,
∴∠C+∠OED=90°,
∵∠PED=∠C.
∴∠PED+∠OED=90°,即∠OEP=90°,
∴OE⊥PE,
∴PE是⊙O的切线;
(2)∵AB为直径,
∴∠AEB=90°,
而AE∥CD,
∴∠EFD=90°,
∴∠FED+∠EDF=90°,
而∠C+∠EDC=90°,
∴∠FED=∠C,
∴∠PED=∠FED,
∴ED平分∠BEP.
4.解:(1)BC、MD的位置关系是平行,
理由:∵∠M=∠D,
∴,
∴∠M=∠MBC,
∴BC∥MD;
(2)连接OC,
∵AB是⊙O的直径,弦CD⊥AB于点E,AE=16,BE=4,
∴∠OEC=90°,EC=ED,AB=AE+BE=20,
∴OC=10,OE=OB﹣BE=6,
∴CE=,
∴CD=2CE=16,
即线段CD的长是16.
5.(1)证明:∵四边形ADCH是圆内接四边形,
∴∠ADC+∠AHC=180°,
又∵∠AHC+∠AHB=180°,
∴∠ADC=∠AHB,
∵四边形ABCD是平行四边形,
∴∠ADC=∠B,
∴∠AHB=∠B,
∴AB=AH,
∴△ABH是等腰三角形;
(2)证明:连接OC,如右图所示,
∵边AB与⊙O相切于点A,
∴BA⊥AF,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴CD⊥AF,
又∵FA经过圆心O,
∴,∠OEC=90°,
∴∠COF=2∠DAF,
又∵∠PCD=2∠DAF,
∴∠COF=∠PCD,
∵∠COF+∠OCE=90°,
∴∠PCD+∠OCE=90°,
即∠OCP=90°,
∴直线PC是⊙O的切线;
(3)∵四边形ABCD是平行四边形,
∴DC=AB=2,
∵FA⊥CD,
∴DE=CE=1,
∵∠AED=90°,AD=,DE=1,
∴AE=,
设⊙O的半径为r,则OA=OD=r,OE=AE﹣OA=4﹣r,
∵∠OED=90°,DE=1,
∴r2=(4﹣r)2+12
解得,r=,
即⊙O的半径是.
6.(1)证明:连结OA.
∵OA=OD,
∴∠ODA=∠OAD.
∵DA平分∠BDE,
∴∠ODA=∠EDA.
∴∠OAD=∠EDA,
∴EC∥OA.
∵AE⊥CD,
∴OA⊥AE.
∵点A在⊙O上,
∴AE是⊙O的切线.
(2)解:过点O作OF⊥CD,垂足为点F.
∵∠OAE=∠AED=∠OFD=90°,
∴四边形AOFE是矩形.
∴OF=AE=8cm.
又∵OF⊥CD,
∴DF=CD=6cm.
在Rt△ODF中,OD==10cm,
即⊙O的半径为10cm.
7.解:(1)∵BC⊥AM,CD⊥AB,
∴∠ENC=∠EFA=90°.
∵∠AEF=∠CEN,
∴∠BAM=∠BCD.
∵AM是⊙O直径,弦BC⊥AM,
∴BN=CN,
∴EB=EC,
∴∠EBC=∠BCD,
∴∠BED=2∠BCD=2∠BAM;
(2)连接AC,如图2,
∵AM是⊙O直径,弦BC⊥AM,
∴=,
∴∠BAM=∠CAM,
∴∠BDC=∠BAC=2∠BAM=∠BED,
∴BD=BE.
在△ABE和△CDB中,
,
∴△ABE≌△CDB,
∴AE=CB.
∵BN=CN,
∴AE=CB=2CN;
(3)过点O作OP⊥AB于P,作OH⊥BE于H,作OQ⊥CD于Q,连接OC,如图3,
则有AP=BP=AB,CQ=DQ=CD.
∵AB=CD,
∴AP=CQ,
∴OP===OQ.
∵AM垂直平分BC,
∴EB=EC,
∴∠BEA=∠CEA.
∵OH⊥BE,OQ⊥CD,
∴OH=OQ,
∴OP=OQ=OH,
∴====.
又∵=,
∴=.
设AO=7k,则EO=4k,
∴AE=AO+EO=11k=11,
∴k=1,
∴AO=7,EO=4,
∴AM=2AO=14,
∴EM=AM﹣AE=14﹣11=3.
8.(1)证明:连接OD,
∵PD切⊙O于点D,
∴OD⊥PD,
∵BE⊥PC,
∴OD∥BE,
∴ADO=∠E,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠E,
∴AB=BE;
(2)解:∵OD∥BE,∠ABC=60°,
∴∠DOP=∠ABC=60°,
∵PD⊥OD,
∴tan∠DOP=,
∴,
∴OD=2,
∴OP=4,
∴PB=6,
∴sin∠ABC=,
∴,
∴PC=3,
∴DC=,
∴DC2+OD2=OC2,
∴()2+22=OC2,
∴OC=.
9.解:(1)连接OC,如图1①,
∵CD为⊙O的切线,
∴OC⊥CD.
∵AD⊥CD,
∴OC∥AD,
∴∠CAD=∠ACO.
又∵OC=OA,
∴∠ACO=∠OAC,
∴∠CAD=∠OAC,
∴AC平分∠DAB;
(2)连接BC、EC、OC,如图1②,
设AB=5x,则由4AB=5AD可得AD=4x.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ADC=∠ACB=90°.
∵∠DAC=∠CAB,
∴△ADC∽△ACB,
∴=,
∴AC2=AD?AB=20x2,
∴DC2=AC2﹣AD2=20x2﹣16x2=4x2.
∵直线CD与⊙O相切,
∴根据切割线定理可得CD2=DE?DA,
∴4x2=DE?4x,
∴DE=x,
∴AE=3x=3DE;
(3)过点A作AH⊥FC,连接AF,如图2,
∵AB=5x=10,
∴OA=OF=5,x=2,
∴AC2=20x2=80,
∴AC=4.
∵∠ACF=45°,
∴AH=AC?sin∠ACH=4×=2,
CH=AC?cos∠ACH=4×=2.
∵∠AOF=2∠ACF=90°,
∴AF==5,
∴FH==,
∴FC=CH+FH=3,
即CF的长为3.
10.(1)证明:∵AB是⊙O的直径,
∴∠ADB=∠90°,
∵BC是⊙O的切线,
∴∠OBC=∠90°,
∵AD∥CO,
∴∠A=∠COB,
在△ABD和△OBC中
∵∠ADB=∠OBC,∠A=∠COB,
∴△ABD∽△OCB;
(2)由(1)知,△ABD∽△OCB,
∴=,即AD=,
∵AB=2,BC=,
∴OB=1,
∴OC==,
∴AD==.
