人教版数学八年级下册18.2.1《矩形》精选练习 (word含答案)
文档属性
| 名称 | 人教版数学八年级下册18.2.1《矩形》精选练习 (word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 148.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 11:08:30 | ||
图片预览



文档简介
18.2.1《矩形》精选练习
一、选择题
1.如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AC=16,则图中长度为8的线段有( )
A.2条??
?
B.4条??
?
C.5条??
?
D.6条
2.如图,矩形ABCD的对角线AC和BD相交于点O,若∠AOD=120°,AC=10,则AB的长为( )
A.10?????
B.8??????
C.6??????
D.5
3.已知矩形ABCD的周长为20cm,两条对角线AC,BD相交于点O,过点O作AC的垂线EF,分别交两边AD,BC于E,F(不与顶点重合),则以下关于△CDE与△ABF判断完全正确的一项为( )
A.
它们周长都等于10cm,但面积不一定相等?
B.
它们全等,且周长都为10cm
C.
它们全等,且周长都为5cm????
D.
它们全等,但周长和面积都不能确定
4.如图,在四边形ABCD中,AC与BD相交于点O,∠BAD=90°,BO=DO,那么添加下列一个条件后,仍不能判定四边形ABCD是矩形的是( )
A.∠ABC=90°??
B.∠BCD=90°??
C.AB=CD????
D.AB∥CD
5.已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是(
?
?)
A.3?
B.4??
?
C.5?
??
D.6
6.如图,将矩形ABCD沿对角线BD折叠,点A落在点E处,DE交BC于点F,若∠CFD=40°,则∠ABD的度数为( )
A.50°??
?
B.60°??
?
C.70°?
??
D.80°
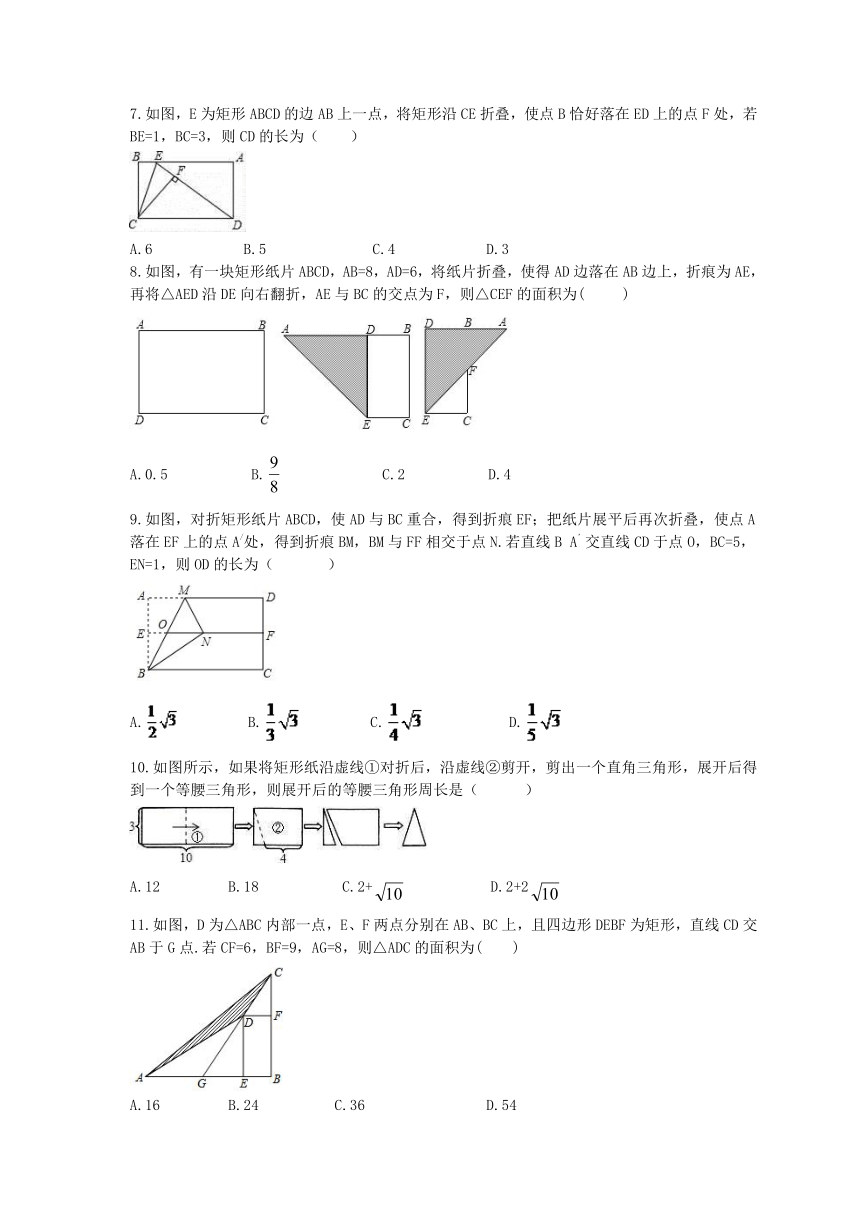
7.如图,E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为( )
A.6???
??
B.5????
??
C.4??
???
D.3
8.如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为(
)
A.0.5?
????B.
?
?C.2?
????D.4
9.如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF上的点A/处,得到折痕BM,BM与FF相交于点N.若直线B
A’交直线CD于点O,BC=5,EN=1,则OD的长为(???
)
A.????
B.????
C.?????
D.
10.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形,则展开后的等腰三角形周长是(
)
A.12????
B.18?????
C.2+?????
D.2+2
11.如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为( )
A.16????
B.24???
?
C.36????
???
D.54
12.矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )
A.1??????
B.?????
C.???
D.
二
、填空题
13.如图,在矩形ABCD中,对角线AC,BC相交于点O,已知∠BOC=120°,DC=3cm,则AC的长为________cm.
14.如图,在矩形ABCD中,AD=4,AB=8.分别以点B,D为圆心,以大于BD的长为半径画弧,两弧相交于点E和F.作直线EF分别与DC,DB,AB交于点M,O,N,则MN=__________.
15.如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使2CF=BC.若AB=10,则EF的长是__________.?
16.如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为______cm2.
17.如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C/,BC/与AD交于点E,若AB=3,BC=4,则DE的长为_________.
18.如图,矩形ABCD中,E、F分别为AB、CD的中点.G为AD上一点,将△ABG沿BG翻折,使A点的对应点恰好落在EF上,则∠ABG= ??
.
???
三
、解答题
19.如图,△ABC中,AB=AC,AD是BC边上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE是矩形;
(2)若BC=6,∠DOC=60°,求四边形ADCE的面积.
20.如图,在矩形ABCD中,过对角线BD的中点O作BD的垂线EF,分别交AD,BC于点E,F.
(1)求证:△DOE≌△BOF;
(2)若AB=6,AD=8,连接BE,DF,求四边形BFDE的周长.
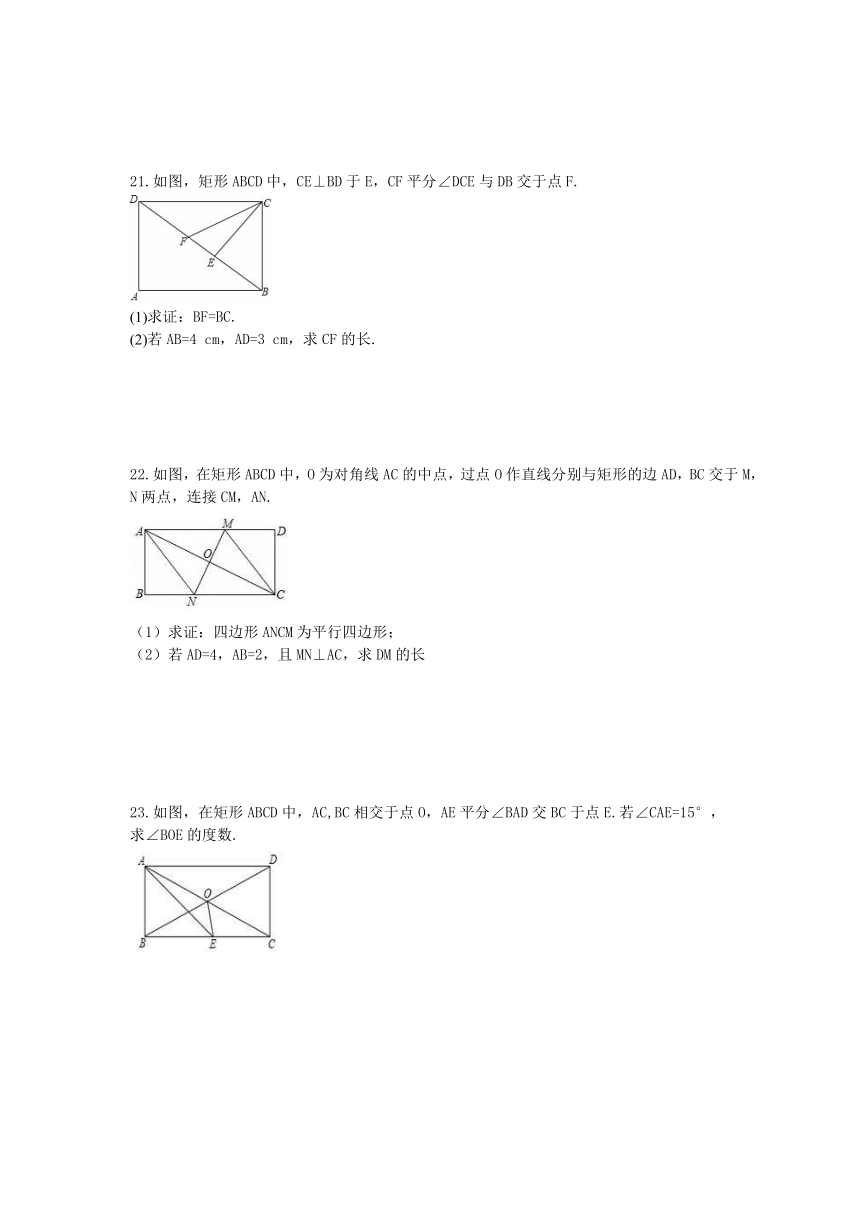
21.如图,矩形ABCD中,CE⊥BD于E,CF平分∠DCE与DB交于点F.
(1)求证:BF=BC.
(2)若AB=4
cm,AD=3
cm,求CF的长.
22.如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD,BC交于M,N两点,连接CM,AN.
(1)求证:四边形ANCM为平行四边形;
(2)若AD=4,AB=2,且MN⊥AC,求DM的长
23.如图,在矩形ABCD中,AC,BC相交于点O,AE平分∠BAD交BC于点E.若∠CAE=15°,
求∠BOE的度数.
24.如图,将长方形ABCD沿对角线AC折叠,使点B落在E处,若AB=3,BC=4,则:
(1)试判断折叠后重叠部分三角形的形状,并证明;
(2)求重叠部分的面积.
参考答案
1.答案为:D
2.答案为:D
3.答案为:B
4.答案为:C
5.答案为:C
6.答案为:C
7.答案为:B
8.答案为:C.
9.答案为:B
10.答案为:D
11.答案为:B
12.答案为:C
13.答案为:6cm
14.答案为:2.
15.答案为:5.
16.答案为:12.5或5或10.
17.答案为:
18.答案为:30°.
19.(1)证明:∵点O是AC中点,
∴OA=OC,
又∵OE=OD,
∴四边形ADCE是平行四边形.
∵AD是BC边上的高,
∴∠ADC=90°,
∴四边形ADCE的是矩形.
(2)解:∵AD是等腰三角形BC边上的高,BC=6,
∴BD=DC=3
∵四边形ADCE的是矩形,
∴OD=OC=0.5AC.
∵∠DOC=60°,
∴△DOC是等边三角形,
∴OC=DC=3,
∴AC=6.
在Rt△ADC中,∠ADC=90°,DC=3,AC=6,
由勾股定理得
AD=,
∴四边形ADCE的面积S=AD×DC=3×=.
20.解:(1)∵四边形ABCD是矩形,
∴,,
∴,
又∵,
∴,
在△DOE和△BOF中,
,
∴.
(2)由(1)可得,,,
∴四边形BFDE是平行四边形,
在△EBO和△EDO中,
,
∴,
∴,
∴四边形BFDE是菱形,
根据,设,可得,
在Rt△ABE中,根据勾股定理可得:,
即,解得:,
∴,
∴四边形BFDE的周长=25.
21.
(1)证明:∵四边形ABCD是矩形,∴∠BCD=90°,
∴∠CDB+∠DBC=90°,
∵CE⊥BD,
∴∠DBC+∠ECB=90°,
∴∠ECB=∠CDB.
∵∠CFB=∠CDB+∠DCF,∠BCF=∠ECB+∠ECF,∠DCF=∠ECF,
∴∠CFB=∠BCF,
∴BF=BC.
(2)解:∵四边形ABCD是矩形,∴DC=AB=4,BC=AD=3.
在Rt△BCD中,由勾股定理得BD=5
又∵BD·CE=BC·DC,
∴CE=2.4
∴BE=1.8
∴EF=BF-BE=1.2.
∴CF=cm
22.(1)证明:∵四边形ABCD是矩形
∴AD//BC,AM//NC
∴
在△AOM和△CON中
∴△AOM△CON
∴AM=NC
又∵
∴四边形ANCM为平行四边形.
(2)∵四边形ANCM为平行四边形
∵
∴平行四边形ANCM是菱形
∴AM=AN=NC
∵AD=BC=4
设BN的长度为x
在Rt△ABN中,AB=2,AN=4-x
x=1.5
AN=AM=2.5
∴DM=1.5.
23.解:因为
平分,
所以.
又因为,
所以
因为,
所以△为等边三角形,
所以
因为,
所以△为等腰直角三角形,
所以.
所以,,,
此时.
24.解:(1)△AFC是等腰三角形.
理由如下:∵AD∥BC,
∴∠DAC=∠ACB,
由图形折叠的性质可得到∠ACB=∠ACE,
∴∠DAC=∠ACE.
故△AFC是等腰三角形.
(2)设AF=CF=x,则FD=4﹣x,
在Rt△CDF中,
(4﹣x)2+32=x2,解得:x=,AF=,
∴S△AFC=AF×CD=××3=.故重叠部分面积为.
一、选择题
1.如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AC=16,则图中长度为8的线段有( )
A.2条??
?
B.4条??
?
C.5条??
?
D.6条
2.如图,矩形ABCD的对角线AC和BD相交于点O,若∠AOD=120°,AC=10,则AB的长为( )
A.10?????
B.8??????
C.6??????
D.5
3.已知矩形ABCD的周长为20cm,两条对角线AC,BD相交于点O,过点O作AC的垂线EF,分别交两边AD,BC于E,F(不与顶点重合),则以下关于△CDE与△ABF判断完全正确的一项为( )
A.
它们周长都等于10cm,但面积不一定相等?
B.
它们全等,且周长都为10cm
C.
它们全等,且周长都为5cm????
D.
它们全等,但周长和面积都不能确定
4.如图,在四边形ABCD中,AC与BD相交于点O,∠BAD=90°,BO=DO,那么添加下列一个条件后,仍不能判定四边形ABCD是矩形的是( )
A.∠ABC=90°??
B.∠BCD=90°??
C.AB=CD????
D.AB∥CD
5.已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是(
?
?)
A.3?
B.4??
?
C.5?
??
D.6
6.如图,将矩形ABCD沿对角线BD折叠,点A落在点E处,DE交BC于点F,若∠CFD=40°,则∠ABD的度数为( )
A.50°??
?
B.60°??
?
C.70°?
??
D.80°
7.如图,E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为( )
A.6???
??
B.5????
??
C.4??
???
D.3
8.如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为(
)
A.0.5?
????B.
?
?C.2?
????D.4
9.如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF上的点A/处,得到折痕BM,BM与FF相交于点N.若直线B
A’交直线CD于点O,BC=5,EN=1,则OD的长为(???
)
A.????
B.????
C.?????
D.
10.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形,则展开后的等腰三角形周长是(
)
A.12????
B.18?????
C.2+?????
D.2+2
11.如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为( )
A.16????
B.24???
?
C.36????
???
D.54
12.矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )
A.1??????
B.?????
C.???
D.
二
、填空题
13.如图,在矩形ABCD中,对角线AC,BC相交于点O,已知∠BOC=120°,DC=3cm,则AC的长为________cm.
14.如图,在矩形ABCD中,AD=4,AB=8.分别以点B,D为圆心,以大于BD的长为半径画弧,两弧相交于点E和F.作直线EF分别与DC,DB,AB交于点M,O,N,则MN=__________.
15.如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使2CF=BC.若AB=10,则EF的长是__________.?
16.如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为______cm2.
17.如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C/,BC/与AD交于点E,若AB=3,BC=4,则DE的长为_________.
18.如图,矩形ABCD中,E、F分别为AB、CD的中点.G为AD上一点,将△ABG沿BG翻折,使A点的对应点恰好落在EF上,则∠ABG= ??
.
???
三
、解答题
19.如图,△ABC中,AB=AC,AD是BC边上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE是矩形;
(2)若BC=6,∠DOC=60°,求四边形ADCE的面积.
20.如图,在矩形ABCD中,过对角线BD的中点O作BD的垂线EF,分别交AD,BC于点E,F.
(1)求证:△DOE≌△BOF;
(2)若AB=6,AD=8,连接BE,DF,求四边形BFDE的周长.
21.如图,矩形ABCD中,CE⊥BD于E,CF平分∠DCE与DB交于点F.
(1)求证:BF=BC.
(2)若AB=4
cm,AD=3
cm,求CF的长.
22.如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD,BC交于M,N两点,连接CM,AN.
(1)求证:四边形ANCM为平行四边形;
(2)若AD=4,AB=2,且MN⊥AC,求DM的长
23.如图,在矩形ABCD中,AC,BC相交于点O,AE平分∠BAD交BC于点E.若∠CAE=15°,
求∠BOE的度数.
24.如图,将长方形ABCD沿对角线AC折叠,使点B落在E处,若AB=3,BC=4,则:
(1)试判断折叠后重叠部分三角形的形状,并证明;
(2)求重叠部分的面积.
参考答案
1.答案为:D
2.答案为:D
3.答案为:B
4.答案为:C
5.答案为:C
6.答案为:C
7.答案为:B
8.答案为:C.
9.答案为:B
10.答案为:D
11.答案为:B
12.答案为:C
13.答案为:6cm
14.答案为:2.
15.答案为:5.
16.答案为:12.5或5或10.
17.答案为:
18.答案为:30°.
19.(1)证明:∵点O是AC中点,
∴OA=OC,
又∵OE=OD,
∴四边形ADCE是平行四边形.
∵AD是BC边上的高,
∴∠ADC=90°,
∴四边形ADCE的是矩形.
(2)解:∵AD是等腰三角形BC边上的高,BC=6,
∴BD=DC=3
∵四边形ADCE的是矩形,
∴OD=OC=0.5AC.
∵∠DOC=60°,
∴△DOC是等边三角形,
∴OC=DC=3,
∴AC=6.
在Rt△ADC中,∠ADC=90°,DC=3,AC=6,
由勾股定理得
AD=,
∴四边形ADCE的面积S=AD×DC=3×=.
20.解:(1)∵四边形ABCD是矩形,
∴,,
∴,
又∵,
∴,
在△DOE和△BOF中,
,
∴.
(2)由(1)可得,,,
∴四边形BFDE是平行四边形,
在△EBO和△EDO中,
,
∴,
∴,
∴四边形BFDE是菱形,
根据,设,可得,
在Rt△ABE中,根据勾股定理可得:,
即,解得:,
∴,
∴四边形BFDE的周长=25.
21.
(1)证明:∵四边形ABCD是矩形,∴∠BCD=90°,
∴∠CDB+∠DBC=90°,
∵CE⊥BD,
∴∠DBC+∠ECB=90°,
∴∠ECB=∠CDB.
∵∠CFB=∠CDB+∠DCF,∠BCF=∠ECB+∠ECF,∠DCF=∠ECF,
∴∠CFB=∠BCF,
∴BF=BC.
(2)解:∵四边形ABCD是矩形,∴DC=AB=4,BC=AD=3.
在Rt△BCD中,由勾股定理得BD=5
又∵BD·CE=BC·DC,
∴CE=2.4
∴BE=1.8
∴EF=BF-BE=1.2.
∴CF=cm
22.(1)证明:∵四边形ABCD是矩形
∴AD//BC,AM//NC
∴
在△AOM和△CON中
∴△AOM△CON
∴AM=NC
又∵
∴四边形ANCM为平行四边形.
(2)∵四边形ANCM为平行四边形
∵
∴平行四边形ANCM是菱形
∴AM=AN=NC
∵AD=BC=4
设BN的长度为x
在Rt△ABN中,AB=2,AN=4-x
x=1.5
AN=AM=2.5
∴DM=1.5.
23.解:因为
平分,
所以.
又因为,
所以
因为,
所以△为等边三角形,
所以
因为,
所以△为等腰直角三角形,
所以.
所以,,,
此时.
24.解:(1)△AFC是等腰三角形.
理由如下:∵AD∥BC,
∴∠DAC=∠ACB,
由图形折叠的性质可得到∠ACB=∠ACE,
∴∠DAC=∠ACE.
故△AFC是等腰三角形.
(2)设AF=CF=x,则FD=4﹣x,
在Rt△CDF中,
(4﹣x)2+32=x2,解得:x=,AF=,
∴S△AFC=AF×CD=××3=.故重叠部分面积为.
