人教版数学八年级下册18.2.2 菱形 同步练习(word版含答案)
文档属性
| 名称 | 人教版数学八年级下册18.2.2 菱形 同步练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 176.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 11:10:03 | ||
图片预览


文档简介
18.2.2《菱形》精选练习
一、选择题
1.下列命题是真命题的是( )
A.对边相等的四边形为平行四边形
B.对角线互相垂直的平行四边形为正方形
C.邻边相等的四边形是菱形
D.有一个角是90°的平行四边形是矩形
2.下列命题是假命题的是( )
A.四个角相等的四边形是矩形
B.对角线相等的平行四边形是矩形
C.对角线垂直的四边形是菱形
D.对角线垂直的平行四边形是菱形
3.菱形的两条对角线长分别是6和8,则此菱形的周长是(?
)
A.5????????
B.20???????
C.24??????
D.32
4.如图,在菱形ABCD中,E,F分别是AB,AC的中点,若EF=2,则菱形ABCD的周长为( )
A.4??????
B.8??????
C.16?????
D.20
5.如图,菱形ABCD的两条对角线AC,BD相交于点O,若AC=4,BD=6,则菱形ABCD的周长为( )
A.16?????
B.24?????
C.4????
D.8
6.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是(??
)
A.???
??
B.2????
?
C.?????
D.4
7.如图,菱形ABCD中,AC交BD于点O,DE⊥BC于点E,连接OE,若∠ABC=140°,
则∠OED=( )
A.20°?
??
B.30°??
?
C.40°??
?
D.50°
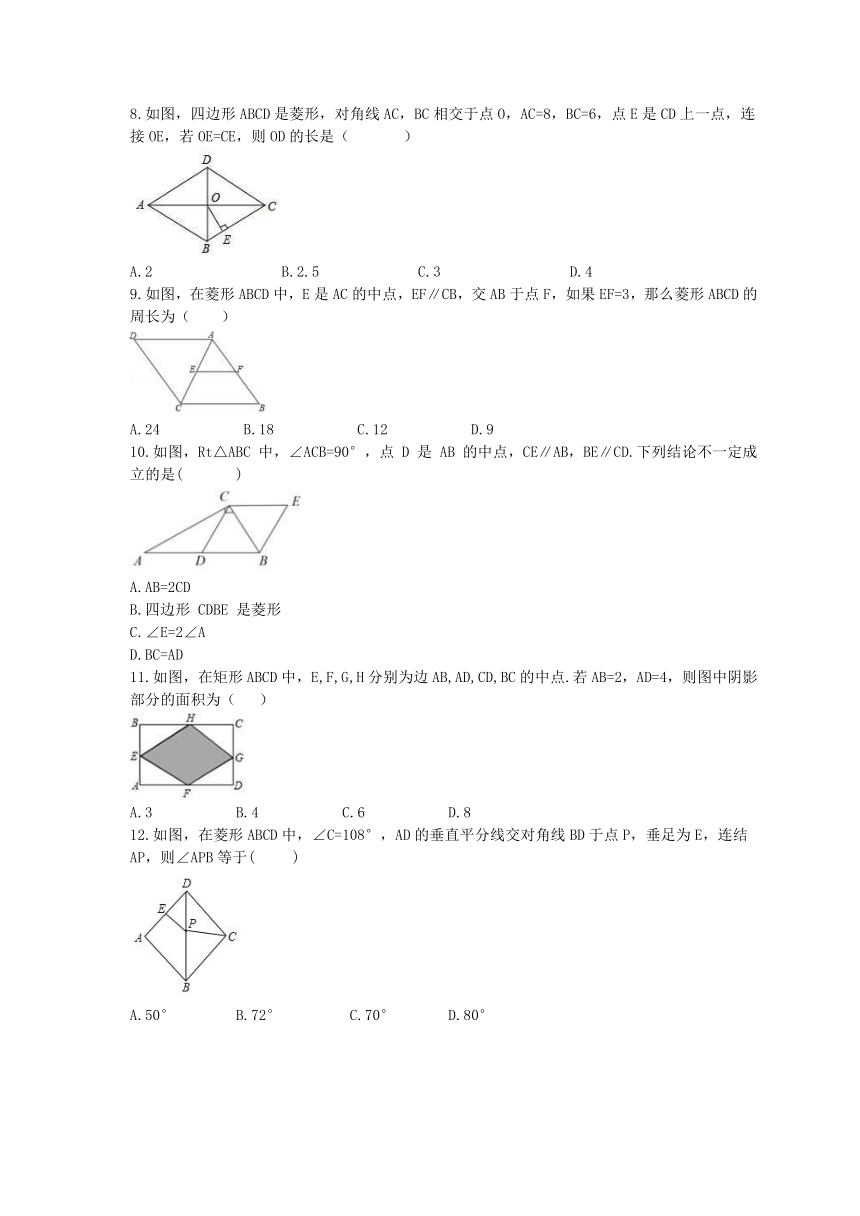
8.如图,四边形ABCD是菱形,对角线AC,BC相交于点O,AC=8,BC=6,点E是CD上一点,连接OE,若OE=CE,则OD的长是(???
)
A.2????????
B.2.5??????
C.3????????
D.4
9.如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为( )
A.24?????
B.18?????
C.12?????
D.9
10.如图,Rt△ABC
中,∠ACB=90°,点
D
是
AB
的中点,CE∥AB,BE∥CD.下列结论不一定成立的是(
)
A.AB=2CD
B.四边形
CDBE
是菱形
C.∠E=2∠A
D.BC=AD
11.如图,在矩形ABCD中,E,F,G,H分别为边AB,AD,CD,BC的中点.若AB=2,AD=4,则图中阴影部分的面积为(?
)
A.3?????
B.4??
???C.6?????
D.8??
12.如图,在菱形ABCD中,∠C=108°,AD的垂直平分线交对角线BD于点P,垂足为E,连结AP,则∠APB等于(
)
A.50°
?
B.72°?
?
C.70°?
D.80°
二、填空题
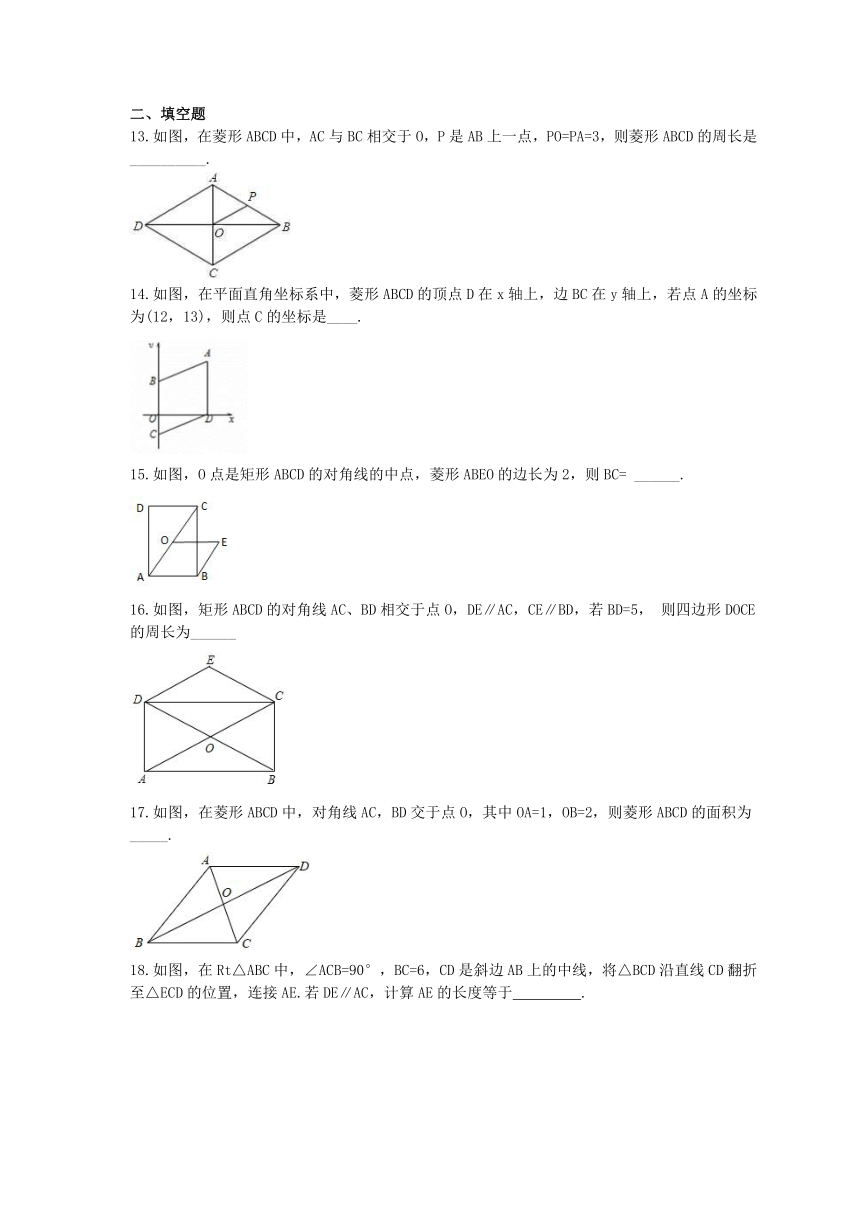
13.如图,在菱形ABCD中,AC与BC相交于O,P是AB上一点,PO=PA=3,则菱形ABCD的周长是__________.
14.如图,在平面直角坐标系中,菱形ABCD的顶点D在x轴上,边BC在y轴上,若点A的坐标为(12,13),则点C的坐标是____.
15.如图,O点是矩形ABCD的对角线的中点,菱形ABEO的边长为2,则BC=
______.
16.如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD,若BD=5,
则四边形DOCE的周长为______
17.如图,在菱形ABCD中,对角线AC,BD交于点O,其中OA=1,OB=2,则菱形ABCD的面积为_____.
18.如图,在Rt△ABC中,∠ACB=90°,BC=6,CD是斜边AB上的中线,将△BCD沿直线CD翻折至△ECD的位置,连接AE.若DE∥AC,计算AE的长度等于 ??
.
三、解答题
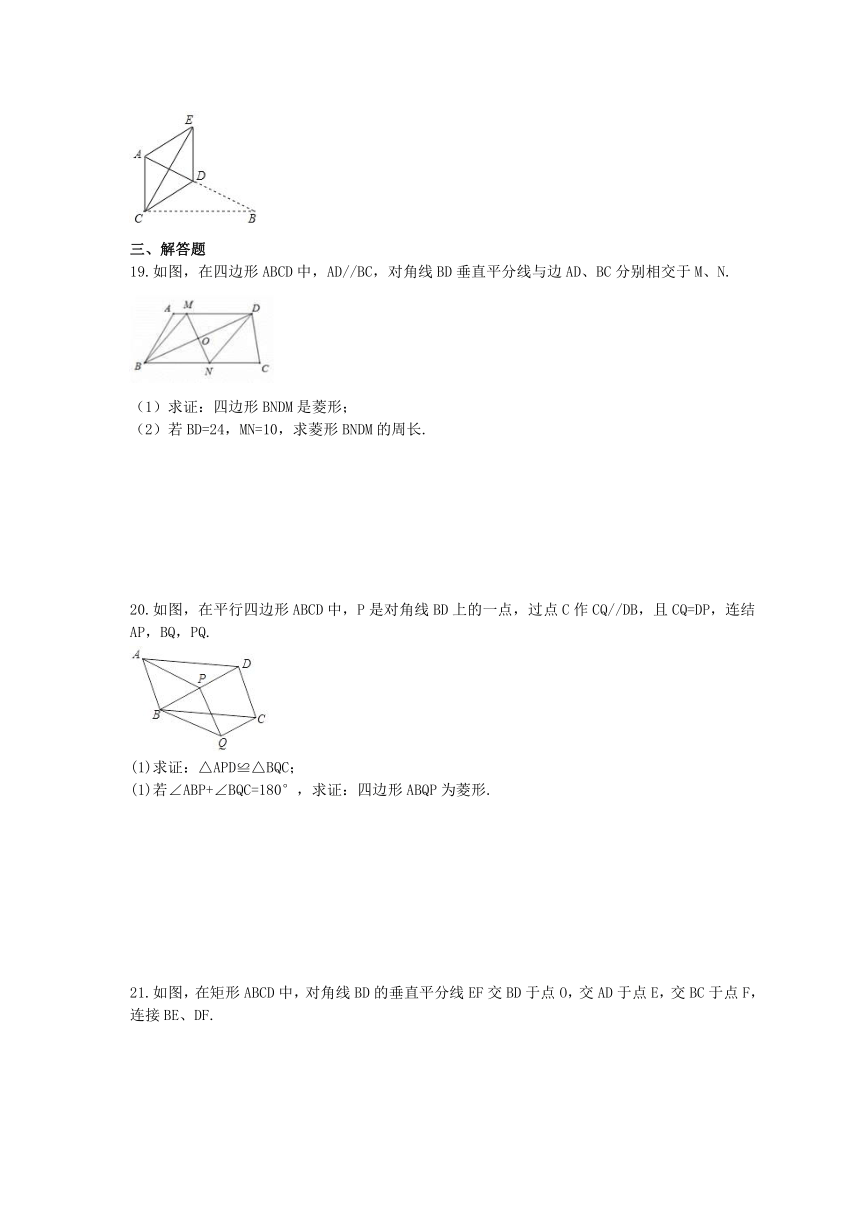
19.如图,在四边形ABCD中,AD//BC,对角线BD垂直平分线与边AD、BC分别相交于M、N.
(1)求证:四边形BNDM是菱形;
(2)若BD=24,MN=10,求菱形BNDM的周长.
20.如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ//DB,且CQ=DP,连结AP,BQ,PQ.
(1)求证:△APD≌△BQC;
(1)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.
21.如图,在矩形ABCD中,对角线BD的垂直平分线EF交BD于点O,交AD于点E,交BC于点F,连接BE、DF.
①求证:四边形BFDE是菱形;
②若AB=3,AD=6,求菱形BFDE的面积.
22.如图,在“飞镖形”ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)求证:四边形EFGH是平行四边形;
(2)“飞镖形”ABCD满足条件______时,四边形EFGH是菱形.
23.如图,已知在□ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG//BD交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
24.如图,已知在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.
参考答案
1.答案为:D
2.答案为:C
3.答案为:B
4.答案为:C
5.答案为:C
6.答案为:A
7.答案为:A
8.答案为:B
9.答案为:A
10.答案为:D
11.答案为:B.
12.答案为:B
13.答案为:24.
14.答案为:C(0,-5)
15.答案为:2
16.答案为:10.
17.答案为:4.
18.答案为:.
19.(1)∵,∴.
∵是对角线的垂直平分线,
∴,.
在和中,,
∴,
∴,
∴四边形BNDM为平行四边形.
又∵,
∴四边形BNDM为菱形.
(2)∵四边形BNDM为菱形,,.
∴,,.
在中,.
∴菱形BNDM的周长52.
20.
(1)证明:∵四边形ABCD是平行四边形,
21.①证明:∵四边形ABCD是矩形,
∴AD∥BC,?
∠A=900
∴∠EDO=∠FBO,
∵EF是BD的垂直平分线,
∴BO=DO,EF⊥BD
在△DEO和△BFO中,,
∴△DEO≌△BFO(ASA),
∴OE=OF
∵OB=OD
∴四边形BEDF是平行四边形,
∵EF⊥BD,∴平行四边形BFDE是菱形;
②解:设AE=x,则DE=6-x,
由①得四边形BFDE是菱形,∴BE=DE=6-x,
∵∠A=900.∴AE2+AB2=BE2
22.证明:
23.(1)证明:∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=0.5AB,CF=0.5CD.
∴AE=CF.
∴△ADE≌△CBF(SAS).
(2)解:当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∴AE=BE,
∴AE=BE=DE.
24.
(1)解:∵四边形ABCD是菱形,
∴CB=CD,AB∥CD,
∴∠1=∠ACD.
∵∠1=∠2,
∴∠2=∠ACD,
∴MC=MD.
∵ME⊥CD,
∴CD=2CE=2,
∴BC=CD=2.
(2)证明:如图,延长DF交AB的延长线于点G.
∵四边形ABCD是菱形,
∴∠BCA=∠DCA,BC=CD.
∵BC=2CF,CD=2CE,
∴CE=CF.
∵CM=CM,
∴△CEM≌△CFM,
∴ME=MF.
∵AB∥CD,
∴∠2=∠G,∠BCD=∠GBF.
∵CF=BF,
∴△CDF≌△BGF,
∴DF=GF.
∵∠1=∠2,∠G=∠2,
∴∠1=∠G,
∴AM=GM=MF+GF=DF+ME.
一、选择题
1.下列命题是真命题的是( )
A.对边相等的四边形为平行四边形
B.对角线互相垂直的平行四边形为正方形
C.邻边相等的四边形是菱形
D.有一个角是90°的平行四边形是矩形
2.下列命题是假命题的是( )
A.四个角相等的四边形是矩形
B.对角线相等的平行四边形是矩形
C.对角线垂直的四边形是菱形
D.对角线垂直的平行四边形是菱形
3.菱形的两条对角线长分别是6和8,则此菱形的周长是(?
)
A.5????????
B.20???????
C.24??????
D.32
4.如图,在菱形ABCD中,E,F分别是AB,AC的中点,若EF=2,则菱形ABCD的周长为( )
A.4??????
B.8??????
C.16?????
D.20
5.如图,菱形ABCD的两条对角线AC,BD相交于点O,若AC=4,BD=6,则菱形ABCD的周长为( )
A.16?????
B.24?????
C.4????
D.8
6.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是(??
)
A.???
??
B.2????
?
C.?????
D.4
7.如图,菱形ABCD中,AC交BD于点O,DE⊥BC于点E,连接OE,若∠ABC=140°,
则∠OED=( )
A.20°?
??
B.30°??
?
C.40°??
?
D.50°
8.如图,四边形ABCD是菱形,对角线AC,BC相交于点O,AC=8,BC=6,点E是CD上一点,连接OE,若OE=CE,则OD的长是(???
)
A.2????????
B.2.5??????
C.3????????
D.4
9.如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为( )
A.24?????
B.18?????
C.12?????
D.9
10.如图,Rt△ABC
中,∠ACB=90°,点
D
是
AB
的中点,CE∥AB,BE∥CD.下列结论不一定成立的是(
)
A.AB=2CD
B.四边形
CDBE
是菱形
C.∠E=2∠A
D.BC=AD
11.如图,在矩形ABCD中,E,F,G,H分别为边AB,AD,CD,BC的中点.若AB=2,AD=4,则图中阴影部分的面积为(?
)
A.3?????
B.4??
???C.6?????
D.8??
12.如图,在菱形ABCD中,∠C=108°,AD的垂直平分线交对角线BD于点P,垂足为E,连结AP,则∠APB等于(
)
A.50°
?
B.72°?
?
C.70°?
D.80°
二、填空题
13.如图,在菱形ABCD中,AC与BC相交于O,P是AB上一点,PO=PA=3,则菱形ABCD的周长是__________.
14.如图,在平面直角坐标系中,菱形ABCD的顶点D在x轴上,边BC在y轴上,若点A的坐标为(12,13),则点C的坐标是____.
15.如图,O点是矩形ABCD的对角线的中点,菱形ABEO的边长为2,则BC=
______.
16.如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD,若BD=5,
则四边形DOCE的周长为______
17.如图,在菱形ABCD中,对角线AC,BD交于点O,其中OA=1,OB=2,则菱形ABCD的面积为_____.
18.如图,在Rt△ABC中,∠ACB=90°,BC=6,CD是斜边AB上的中线,将△BCD沿直线CD翻折至△ECD的位置,连接AE.若DE∥AC,计算AE的长度等于 ??
.
三、解答题
19.如图,在四边形ABCD中,AD//BC,对角线BD垂直平分线与边AD、BC分别相交于M、N.
(1)求证:四边形BNDM是菱形;
(2)若BD=24,MN=10,求菱形BNDM的周长.
20.如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ//DB,且CQ=DP,连结AP,BQ,PQ.
(1)求证:△APD≌△BQC;
(1)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.
21.如图,在矩形ABCD中,对角线BD的垂直平分线EF交BD于点O,交AD于点E,交BC于点F,连接BE、DF.
①求证:四边形BFDE是菱形;
②若AB=3,AD=6,求菱形BFDE的面积.
22.如图,在“飞镖形”ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)求证:四边形EFGH是平行四边形;
(2)“飞镖形”ABCD满足条件______时,四边形EFGH是菱形.
23.如图,已知在□ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG//BD交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
24.如图,已知在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.
参考答案
1.答案为:D
2.答案为:C
3.答案为:B
4.答案为:C
5.答案为:C
6.答案为:A
7.答案为:A
8.答案为:B
9.答案为:A
10.答案为:D
11.答案为:B.
12.答案为:B
13.答案为:24.
14.答案为:C(0,-5)
15.答案为:2
16.答案为:10.
17.答案为:4.
18.答案为:.
19.(1)∵,∴.
∵是对角线的垂直平分线,
∴,.
在和中,,
∴,
∴,
∴四边形BNDM为平行四边形.
又∵,
∴四边形BNDM为菱形.
(2)∵四边形BNDM为菱形,,.
∴,,.
在中,.
∴菱形BNDM的周长52.
20.
(1)证明:∵四边形ABCD是平行四边形,
21.①证明:∵四边形ABCD是矩形,
∴AD∥BC,?
∠A=900
∴∠EDO=∠FBO,
∵EF是BD的垂直平分线,
∴BO=DO,EF⊥BD
在△DEO和△BFO中,,
∴△DEO≌△BFO(ASA),
∴OE=OF
∵OB=OD
∴四边形BEDF是平行四边形,
∵EF⊥BD,∴平行四边形BFDE是菱形;
②解:设AE=x,则DE=6-x,
由①得四边形BFDE是菱形,∴BE=DE=6-x,
∵∠A=900.∴AE2+AB2=BE2
22.证明:
23.(1)证明:∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=0.5AB,CF=0.5CD.
∴AE=CF.
∴△ADE≌△CBF(SAS).
(2)解:当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∴AE=BE,
∴AE=BE=DE.
24.
(1)解:∵四边形ABCD是菱形,
∴CB=CD,AB∥CD,
∴∠1=∠ACD.
∵∠1=∠2,
∴∠2=∠ACD,
∴MC=MD.
∵ME⊥CD,
∴CD=2CE=2,
∴BC=CD=2.
(2)证明:如图,延长DF交AB的延长线于点G.
∵四边形ABCD是菱形,
∴∠BCA=∠DCA,BC=CD.
∵BC=2CF,CD=2CE,
∴CE=CF.
∵CM=CM,
∴△CEM≌△CFM,
∴ME=MF.
∵AB∥CD,
∴∠2=∠G,∠BCD=∠GBF.
∵CF=BF,
∴△CDF≌△BGF,
∴DF=GF.
∵∠1=∠2,∠G=∠2,
∴∠1=∠G,
∴AM=GM=MF+GF=DF+ME.
