人教版数学八年级下册18.2.3《正方形》精选练习 (word含答案)
文档属性
| 名称 | 人教版数学八年级下册18.2.3《正方形》精选练习 (word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 110.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 11:11:34 | ||
图片预览

文档简介
18.2.3《正方形》精选练习
一、选择题
1.下列命题中,正确的是(
).
A.有一组邻边相等的四边形是菱形
B.对角线互相平分且垂直的四边形是矩形
C.两组邻角相等的四边形是平行四边形
D.对角线互相垂直且相等的平行四边形是正方形
2.下列命题是真命题的是( )
A.四边都相等的四边形是矩形?
B.菱形的对角线相等?
C.对角线互相垂直的平行四边形是正方形
D.对角线相等的平行四边形是矩形
3.如图,在正方形ABCD外侧作等边三角形ADE,AC,BE相交于点F,则∠BFC为
( )
A.45°
?B.55°?
C.60°?
.75°
4.下列命题是真命题的是( )
A.菱形的对角线互相平分?
B.一组对边平行,一组对边相等的四边形是平行四边形
C.对角线互相垂直且相等的四边形是正方形?
D.对角线相等的四边形是矩形
5.下列命题中,真命题是(????)
A.有两边相等的平行四边形是菱形
B.对角线垂直的四边形是菱形
C.四个角相等的菱形是正方形
D.两条对角线相等的四边形是矩形
6.下列命题是真命题的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直平分的四边形是正方形
7.如图,已知正方形ABCD边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE长为( )
A.2﹣2
B.﹣1
C.﹣1
D.2﹣
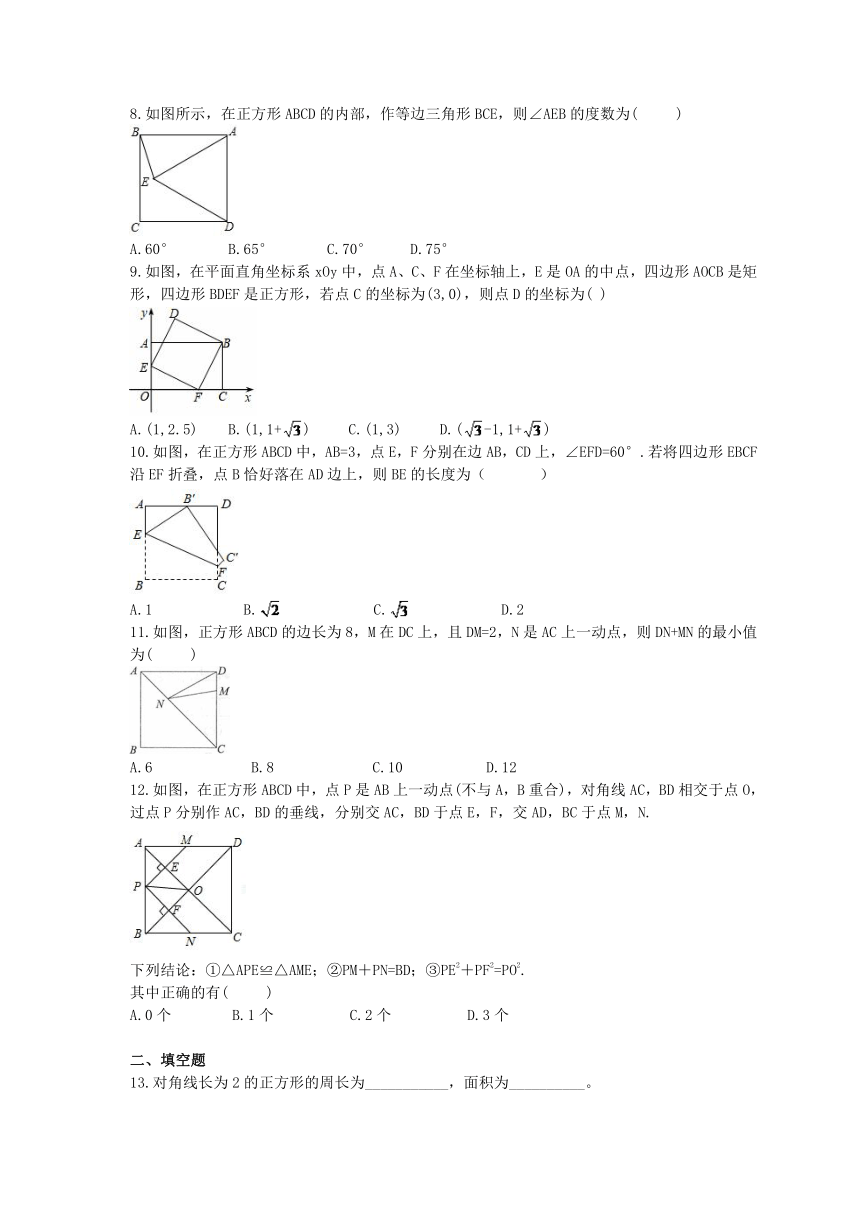
8.如图所示,在正方形ABCD的内部,作等边三角形BCE,则∠AEB的度数为(
)
A.60°
???B.65°?
??C.70°
??D.75°
9.如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为(
)
A.(1,2.5)?
B.(1,1+)
C.(1,3)?
D.(-1,1+)
10.如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长度为(???
)
A.1???
??
B.???
??
C.??
???
D.2
11.如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为(??
)
A.6??????
B.8??????
C.10?????
D.12
12.如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.
下列结论:①△APE≌△AME;②PM+PN=BD;③PE2+PF2=PO2.
其中正确的有(
)
A.0个?
B.1个?
C.2个
?
D.3个
二、填空题
13.对角线长为2的正方形的周长为___________,面积为__________。
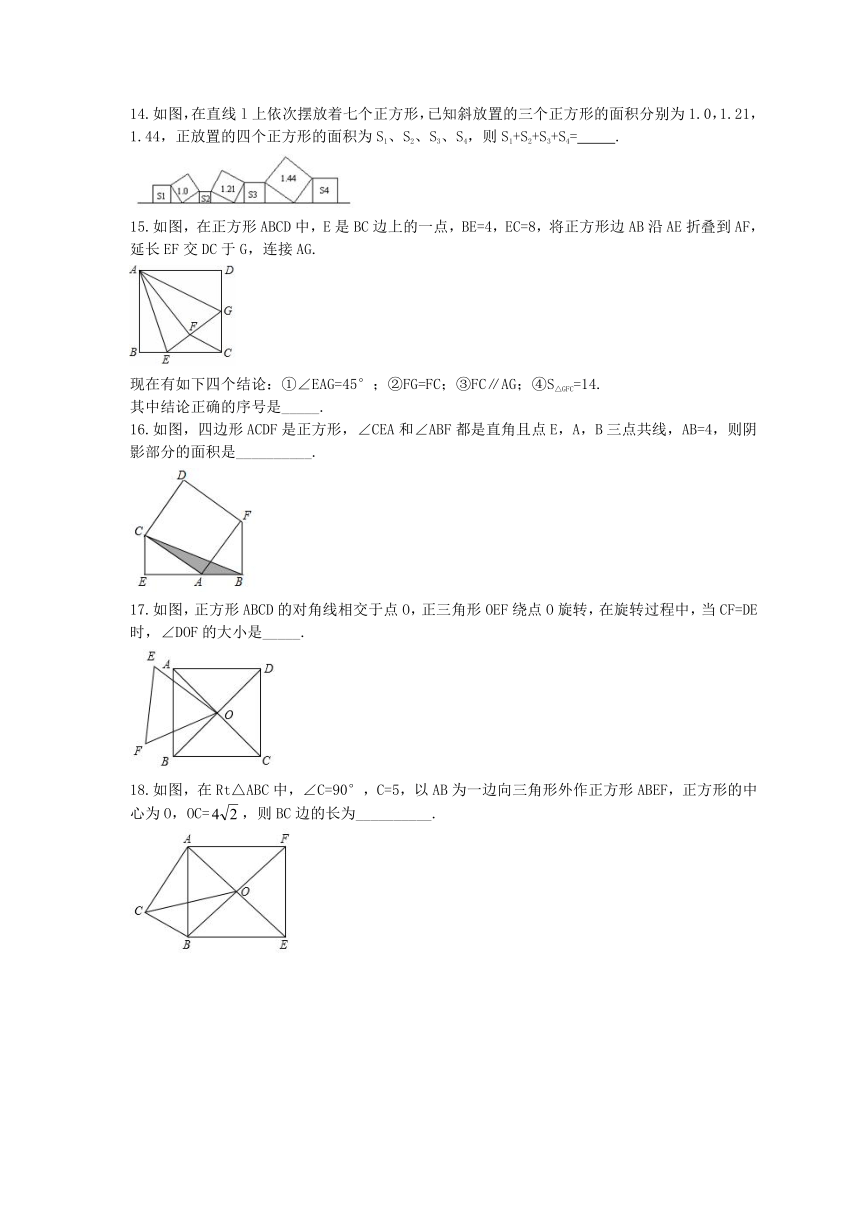
14.如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1.0,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+S2+S3+S4=??
.
15.如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AG.
现在有如下四个结论:①∠EAG=45°;②FG=FC;③FC∥AG;④S△GFC=14.
其中结论正确的序号是_____.
16.如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角且点E,A,B三点共线,AB=4,则阴影部分的面积是__________.
17.如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转,在旋转过程中,当CF=DE时,∠DOF的大小是_____.
18.如图,在Rt△ABC中,∠C=90°,C=5,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,OC=,则BC边的长为__________.
三、解答题
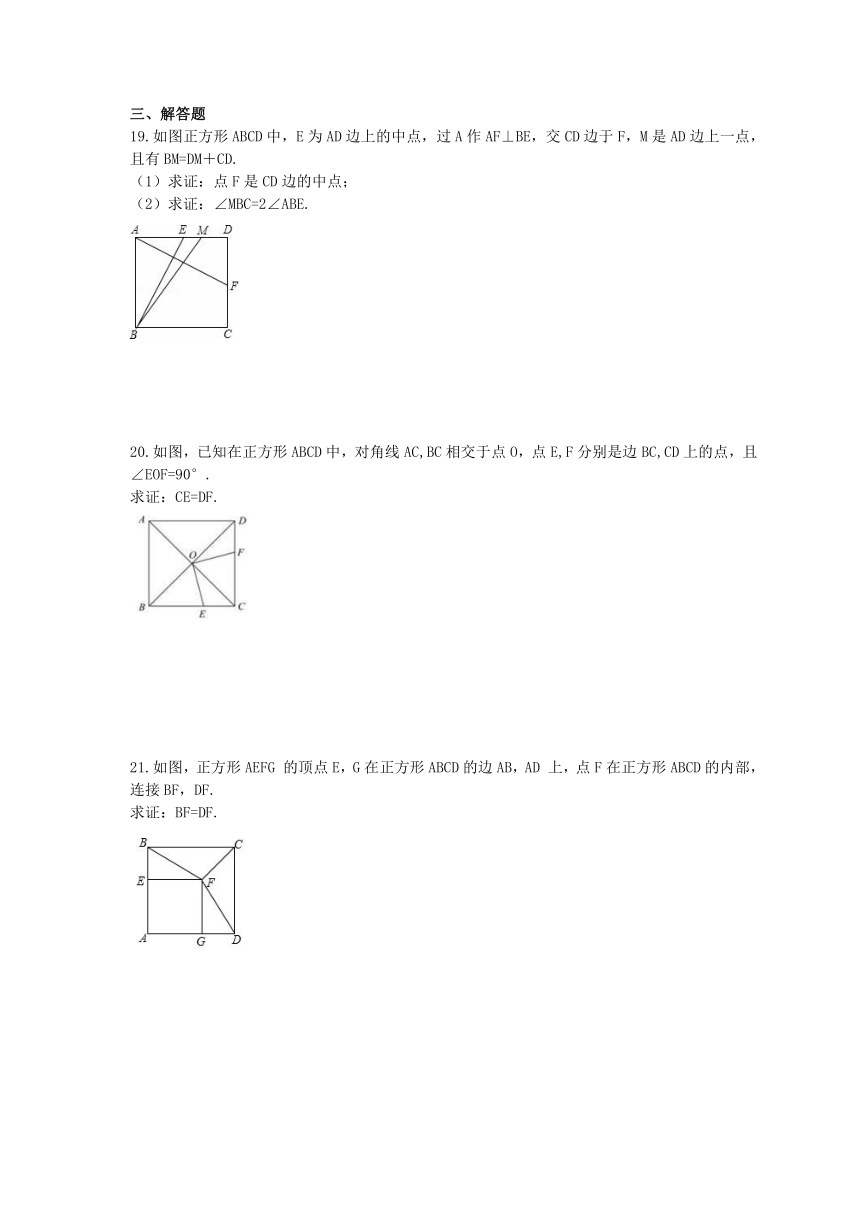
19.如图正方形ABCD中,E为AD边上的中点,过A作AF⊥BE,交CD边于F,M是AD边上一点,且有BM=DM+CD.
(1)求证:点F是CD边的中点;
(2)求证:∠MBC=2∠ABE.
20.如图,已知在正方形ABCD中,对角线AC,BC相交于点O,点E,F分别是边BC,CD上的点,且∠EOF=90°.
求证:CE=DF.
21.如图,正方形AEFG
的顶点E,G在正方形ABCD的边AB,AD
上,点F在正方形ABCD的内部,连接BF,DF.
求证:BF=DF.
22.已知:如图,在△ABC中,AB=AC,D是的BC边的中点,DE⊥AC,DF⊥AB,垂足
分别是E、F.
(1)求证:DE=DF;
(2)只添加一个条件,使四边形EDFA是正方形,并给出证明.
23.已知:如图,点E,F,P,Q分别是正方形ABCD的四条边上的点,并且AF=BP=CQ=DE.
求证:(1)EF=FP=PQ=QE;
(2)四边形EFPQ是正方形.
24.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
参考答案
1.答案为:D
2.答案为:D
3.答案为:C
4.答案为:A?
?
5.答案为:A
6.答案为:A
7.答案为:C??
8.答案为:D
9.答案为:C
10.答案为:D
11.答案为:C
12.答案为:D.
13.答案为:5?
14.答案为:2.44.
15.答案为:①③.
16.答案为:8.
17.答案为:165°或15°.
18.答案为:3.
19.解:(1)∵正方形ABCD,
∴AD=DC=AB=BC,∠C=∠D=∠BAD=90°,AB∥CD,
∵AF⊥BE,
∴∠AOE=90°,
∴∠EAF+∠AEB=90°,∠EAF+∠BAF=90°,
∴∠AEB=∠BAF,
∵AB∥CD,
∴∠BAF=∠AFD,
∴∠AEB=∠AFD,
∵∠BAD=∠D,AB=AD,
∴△BAE≌△ADF,
∴AE=DF,
∵E为AD边上的中点,
∴点F是CD边的中点;
(2)延长AD到G.使MG=MB.连接FG,FB,
∵BM=DM+CD,∴DG=DC=BC,
∵∠GDF=∠C=90°,DF=CF,
∴△FDG≌△FCB(SAS),
∴∠DFG=∠CFB,
∴B,F,G共线,
∵E为AD边上的中点,点F是CD边的中点,AD=CD,
∴AE=CF,
∵AB=BC,∠C=∠BAD=90°,AE=CF,
∴△ABE≌△CBF,
∴∠ABE=∠CBF,
∵AG∥BC,
∴∠AGB=∠CBF=∠ABE,
∴∠MBC=∠AMB=2∠AGB=2∠GBC=2∠ABE,
∴∠MBC=2∠ABE.
20.解:∵四边形ABCD为正方形,
∴OD=OC,∠ODF=∠OCE=45°,∠COD=90°,
∵∠EOF=90°,即∠COE+∠COF=90°,
∴∠COE=∠DOF,
∴△COE≌△DOF(ASA),
∴CE=DF.
21.证明:
22.解:(1)连接AD,
∵AB=AC,D是的BC边的中点,
∴AD是∠BAC的角平分线,
∵DE⊥AC,DF⊥AB,
∴DF=DE;
(2)添加∠BAC=90°,
∵DE⊥AC,DF⊥AB,
∴∠AFD=∠AED=90°,
∴四边形AFDE是矩形,
∵DF=DE,
∴四边形EDFA是正方形.
23.证明:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD,
∵AF=BP=CQ=DE,
∴DF=CE=BQ=AP,
在△APF和△DFE和△CEQ和△BQP中,
,
∴△APF≌△DFE≌△CEQ≌△BQP(SAS),
∴EF=FP=PQ=QE;
(2)∵EF=FP=PQ=QE,
∴四边形EFPQ是菱形,
∵△APF≌△BQP,
∴∠AFP=∠BPQ,
∵∠AFP+∠APF=90°,
∴∠APF+∠BPQ=90°,
∴∠FPQ=90°,
∴四边形EFPQ是正方形.
24.
(1)证明:∵四边形ABCD是正方形,
∴∠B=∠D=90°,AD=AB.
由折叠的性质可知AD=AF,∠AFE=∠D=90°,
∴∠AFG=90°,AB=AF,
∴∠AFG=∠B=90°.
又∵AG=AG,
∴△ABG≌△AFG(HL).
(2)解:∵△ABG≌△AFG,∴BG=FG.
设BG=FG=x,则GC=6-x.
∵
E为CD的中点,∴
CE=DE=EF=3,∴
EG=x+3.
在Rt△ECG中,EC2+GC2=EG2,
即32+(6-x)2=(x+3)2,解得x=2.
∴
BG的长为2.
一、选择题
1.下列命题中,正确的是(
).
A.有一组邻边相等的四边形是菱形
B.对角线互相平分且垂直的四边形是矩形
C.两组邻角相等的四边形是平行四边形
D.对角线互相垂直且相等的平行四边形是正方形
2.下列命题是真命题的是( )
A.四边都相等的四边形是矩形?
B.菱形的对角线相等?
C.对角线互相垂直的平行四边形是正方形
D.对角线相等的平行四边形是矩形
3.如图,在正方形ABCD外侧作等边三角形ADE,AC,BE相交于点F,则∠BFC为
( )
A.45°
?B.55°?
C.60°?
.75°
4.下列命题是真命题的是( )
A.菱形的对角线互相平分?
B.一组对边平行,一组对边相等的四边形是平行四边形
C.对角线互相垂直且相等的四边形是正方形?
D.对角线相等的四边形是矩形
5.下列命题中,真命题是(????)
A.有两边相等的平行四边形是菱形
B.对角线垂直的四边形是菱形
C.四个角相等的菱形是正方形
D.两条对角线相等的四边形是矩形
6.下列命题是真命题的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直平分的四边形是正方形
7.如图,已知正方形ABCD边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE长为( )
A.2﹣2
B.﹣1
C.﹣1
D.2﹣
8.如图所示,在正方形ABCD的内部,作等边三角形BCE,则∠AEB的度数为(
)
A.60°
???B.65°?
??C.70°
??D.75°
9.如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为(
)
A.(1,2.5)?
B.(1,1+)
C.(1,3)?
D.(-1,1+)
10.如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长度为(???
)
A.1???
??
B.???
??
C.??
???
D.2
11.如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为(??
)
A.6??????
B.8??????
C.10?????
D.12
12.如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.
下列结论:①△APE≌△AME;②PM+PN=BD;③PE2+PF2=PO2.
其中正确的有(
)
A.0个?
B.1个?
C.2个
?
D.3个
二、填空题
13.对角线长为2的正方形的周长为___________,面积为__________。
14.如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1.0,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+S2+S3+S4=??
.
15.如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AG.
现在有如下四个结论:①∠EAG=45°;②FG=FC;③FC∥AG;④S△GFC=14.
其中结论正确的序号是_____.
16.如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角且点E,A,B三点共线,AB=4,则阴影部分的面积是__________.
17.如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转,在旋转过程中,当CF=DE时,∠DOF的大小是_____.
18.如图,在Rt△ABC中,∠C=90°,C=5,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,OC=,则BC边的长为__________.
三、解答题
19.如图正方形ABCD中,E为AD边上的中点,过A作AF⊥BE,交CD边于F,M是AD边上一点,且有BM=DM+CD.
(1)求证:点F是CD边的中点;
(2)求证:∠MBC=2∠ABE.
20.如图,已知在正方形ABCD中,对角线AC,BC相交于点O,点E,F分别是边BC,CD上的点,且∠EOF=90°.
求证:CE=DF.
21.如图,正方形AEFG
的顶点E,G在正方形ABCD的边AB,AD
上,点F在正方形ABCD的内部,连接BF,DF.
求证:BF=DF.
22.已知:如图,在△ABC中,AB=AC,D是的BC边的中点,DE⊥AC,DF⊥AB,垂足
分别是E、F.
(1)求证:DE=DF;
(2)只添加一个条件,使四边形EDFA是正方形,并给出证明.
23.已知:如图,点E,F,P,Q分别是正方形ABCD的四条边上的点,并且AF=BP=CQ=DE.
求证:(1)EF=FP=PQ=QE;
(2)四边形EFPQ是正方形.
24.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
参考答案
1.答案为:D
2.答案为:D
3.答案为:C
4.答案为:A?
?
5.答案为:A
6.答案为:A
7.答案为:C??
8.答案为:D
9.答案为:C
10.答案为:D
11.答案为:C
12.答案为:D.
13.答案为:5?
14.答案为:2.44.
15.答案为:①③.
16.答案为:8.
17.答案为:165°或15°.
18.答案为:3.
19.解:(1)∵正方形ABCD,
∴AD=DC=AB=BC,∠C=∠D=∠BAD=90°,AB∥CD,
∵AF⊥BE,
∴∠AOE=90°,
∴∠EAF+∠AEB=90°,∠EAF+∠BAF=90°,
∴∠AEB=∠BAF,
∵AB∥CD,
∴∠BAF=∠AFD,
∴∠AEB=∠AFD,
∵∠BAD=∠D,AB=AD,
∴△BAE≌△ADF,
∴AE=DF,
∵E为AD边上的中点,
∴点F是CD边的中点;
(2)延长AD到G.使MG=MB.连接FG,FB,
∵BM=DM+CD,∴DG=DC=BC,
∵∠GDF=∠C=90°,DF=CF,
∴△FDG≌△FCB(SAS),
∴∠DFG=∠CFB,
∴B,F,G共线,
∵E为AD边上的中点,点F是CD边的中点,AD=CD,
∴AE=CF,
∵AB=BC,∠C=∠BAD=90°,AE=CF,
∴△ABE≌△CBF,
∴∠ABE=∠CBF,
∵AG∥BC,
∴∠AGB=∠CBF=∠ABE,
∴∠MBC=∠AMB=2∠AGB=2∠GBC=2∠ABE,
∴∠MBC=2∠ABE.
20.解:∵四边形ABCD为正方形,
∴OD=OC,∠ODF=∠OCE=45°,∠COD=90°,
∵∠EOF=90°,即∠COE+∠COF=90°,
∴∠COE=∠DOF,
∴△COE≌△DOF(ASA),
∴CE=DF.
21.证明:
22.解:(1)连接AD,
∵AB=AC,D是的BC边的中点,
∴AD是∠BAC的角平分线,
∵DE⊥AC,DF⊥AB,
∴DF=DE;
(2)添加∠BAC=90°,
∵DE⊥AC,DF⊥AB,
∴∠AFD=∠AED=90°,
∴四边形AFDE是矩形,
∵DF=DE,
∴四边形EDFA是正方形.
23.证明:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD,
∵AF=BP=CQ=DE,
∴DF=CE=BQ=AP,
在△APF和△DFE和△CEQ和△BQP中,
,
∴△APF≌△DFE≌△CEQ≌△BQP(SAS),
∴EF=FP=PQ=QE;
(2)∵EF=FP=PQ=QE,
∴四边形EFPQ是菱形,
∵△APF≌△BQP,
∴∠AFP=∠BPQ,
∵∠AFP+∠APF=90°,
∴∠APF+∠BPQ=90°,
∴∠FPQ=90°,
∴四边形EFPQ是正方形.
24.
(1)证明:∵四边形ABCD是正方形,
∴∠B=∠D=90°,AD=AB.
由折叠的性质可知AD=AF,∠AFE=∠D=90°,
∴∠AFG=90°,AB=AF,
∴∠AFG=∠B=90°.
又∵AG=AG,
∴△ABG≌△AFG(HL).
(2)解:∵△ABG≌△AFG,∴BG=FG.
设BG=FG=x,则GC=6-x.
∵
E为CD的中点,∴
CE=DE=EF=3,∴
EG=x+3.
在Rt△ECG中,EC2+GC2=EG2,
即32+(6-x)2=(x+3)2,解得x=2.
∴
BG的长为2.
