北师大版九年级数学下册:2.5.1二次函数和一元二次方程关系课件(共19张PPT)
文档属性
| 名称 | 北师大版九年级数学下册:2.5.1二次函数和一元二次方程关系课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 299.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 21:32:23 | ||
图片预览



文档简介
(共19张PPT)
2.5.1二次函数与一元二次方程
1
19
回顾与思
复习提问
1、一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=______。
当△﹥0时,方程根的情况是______________;
当△=0时,方程根的情况是______________;
当△﹤0时,方程根的情况是______________。
b2-4ac
有两个不等实数根
有两个相等实数根
没有实数根
2、二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)图像是一条_____,它与x轴的交点有几种可能的情况?
抛物线
三种可能:①两个交点
②一个交点
③没有交点。
2
19
设抛物线y=ax?+bx+c(a≠0)与x轴有两个交点,交点坐标如何计算?
(1)二次函数y=x2-5x的图象与x轴的两个交点
的坐标分别是
.
(0,0),(5,0)
(2)若方程ax2+bx+c=0(a≠0)的两根分别是x1=2,x2=3,则抛物线y=ax2+bx+c与x轴的交点坐标分别是__________________.
(2,0),(3,0)
3
19
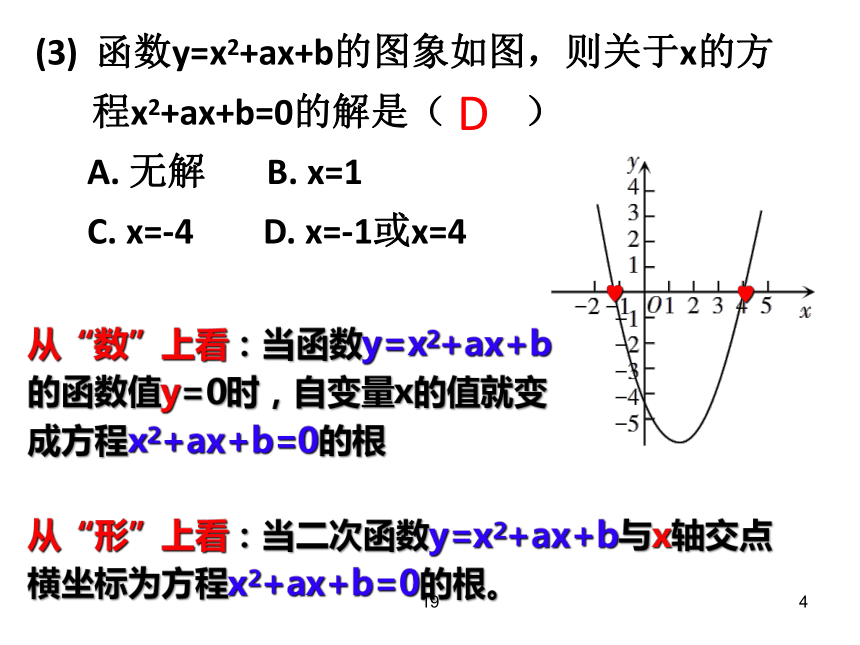
(3)
函数y=x2+ax+b的图象如图,则关于x的方程x2+ax+b=0的解是( )
A.
无解
B.
x=1
C.
x=-4
D.
x=-1或x=4
D
从“数”上看:当函数y=x2+ax+b的函数值y=0时,自变量x的值就变成方程x2+ax+b=0的根
从“形”上看:当二次函数y=x2+ax+b与x轴交点横坐标为方程x2+ax+b=0的根。
?
?
4
19
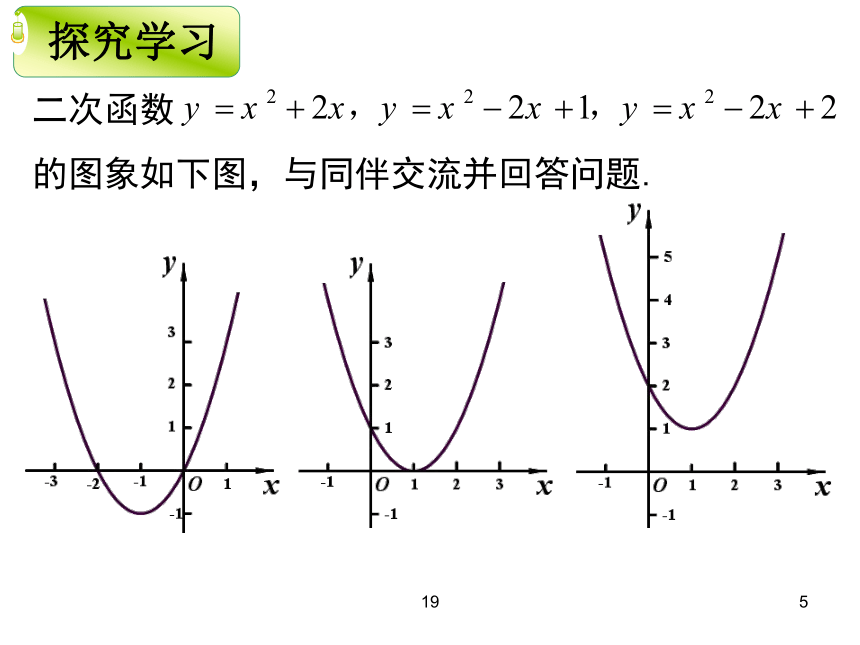
二次函数
的图象如下图,与同伴交流并回答问题.
回顾与思
探究学习
5
19
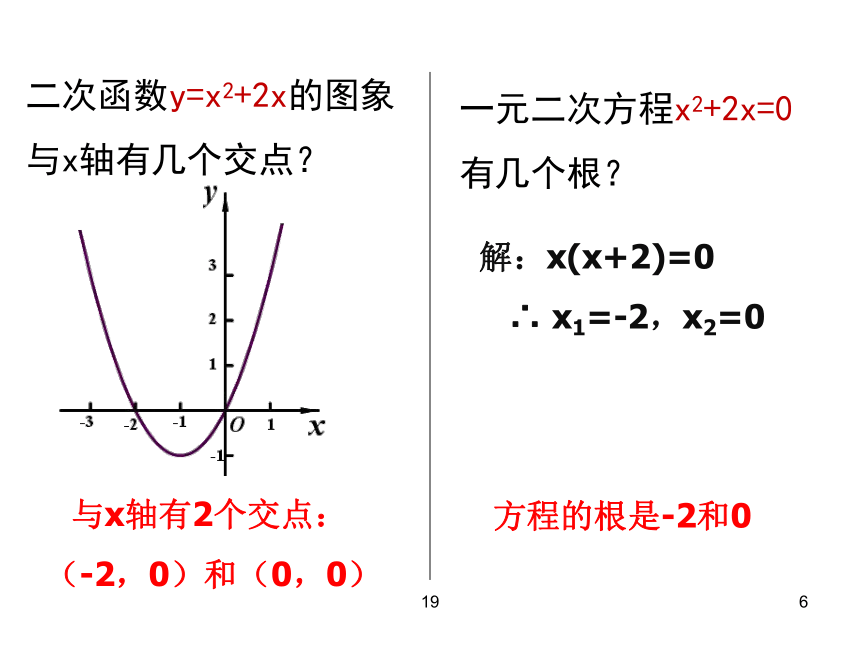
二次函数y=x2+2x的图象
与x轴有几个交点?
与x轴有2个交点:
(-2,0)和(0,0)
一元二次方程x2+2x=0
有几个根?
解:x(x+2)=0
∴
x1=-2,x2=0
方程的根是-2和0
6
19
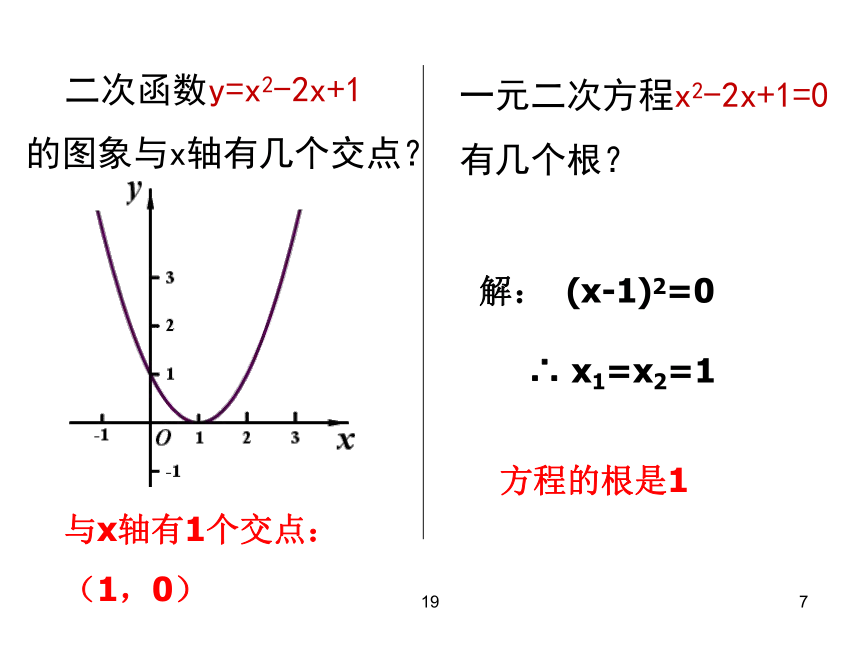
二次函数y=x2-2x+1
的图象与x轴有几个交点?
与x轴有1个交点:
(1,0)
一元二次方程x2-2x+1=0
有几个根?
解:
(x-1)2=0
∴
x1=x2=1
方程的根是1
7
19
二次函数y=x2-2x+2
的图象与x轴有几个交点?
与x轴没有交点
一元二次方程x2-2x+2=0
有几个根?
没有实数根
解:∵△=(-2)2-4×1×2
=-4﹤0
∴
原方程无实根
8
19
归纳总结:
二次函数y=ax2+bx+c的图象和x轴交点
一元二次方程ax2+bx+c=0的根
一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
二次函数y=ax2+bx+c的图象和x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根.
有两个交点
有一个交点
没有交点
有两个相等
的实数根
没有实数根
b2-4ac
>
0
b2-4ac
=
0
b2-4ac
<
0
有两个不相等
的实数根
9
19
所以二次函数与一元二次方程关系密切.
例如,已知二次函数y
=
x2-4x的值为3,求自变量x的值,可以解一元二次方程x2-4x=3(即x2-4x-3=0).
反过来,解方程x2-4x-3=0
又可以看作已知二次函数
y
=
x2-4x-3
的值为0,求自变量x的值.
10
19
(1)抛物线y=x2+3x+2与x轴的交点个数是
(
)
A.
3
B.
2
C.
1
D.
0
(2)抛物线y=2x2+8x+m与x轴只有一个公共点,
则m的值是________.
(3)若抛物线y=ax2+bx+c,当
a>0,c<0时,图象与x轴
的交点情况是
(
)
A.无交点
B.只有一个交点
C.有两个交点
D.不能确定
回顾与思
课堂练习
11
19
(4)(中考)二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①abc<0;
②方程ax2+bx+c=0的根为x1=-1,x2=3;
③当x>1时,y随x值的增大而减小;
④当y>0时,-1<x<3.
其中正确的说法是
(
)
A.①
B.①②
C.①②③
D.①②③④
O
x
y
1
3
-1
12
19
(5)
二次函数y=kx2-2x-1的图象与x轴有交点,则k的取值范围是(
)
A.
k>-1
B.
k≥-1且k≠0
C.
k≥-1
D.
k>-1且k≠0
变式1:已知函数y=(k-3)x2+2x+1的图象与
x轴有交点,求k的取值范围.
变式2:若函数y=mx2+(m+2)x+
m+1的图象与x轴只有一个交点,那么m的值为_________.
13
19
(6)若a>0,b>0,c>0,△>0,那么抛物线y=ax2+bx+c
经过
象限.
一、二、三
(7)若二次函数y=ax2+bx+c的函数值恒为正,则需满足
;
若二次函数y=ax2+bx+c的函数值恒为负,则需满足
.
14
19
(8)如图,函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C.
(1)图象与x轴交点的坐标
是______________
与y轴的交点坐标是_______
(-1,0)和(3,0)
(0,-3)
(2)当x=_______时,y=0;
方程x2-2x-3=0的解是_______;
-1或3
x1=-1,x2=3
15
19
(3)当x满足_____________时,y<0;
当x满足_____________时,y>0;
(4)x2-2x-3<0的解集是___________;
x2-2x-3>0的解集是___________
-1<x<3
x<-1或x>3
-1<x<3
x<-1或x>3
16
19
(9)
已知函数y=mx2-6x+1(m为常数).
(1)求证:无论m为何值,该函数的图象与y轴总有一个固定交点;
(2)若该函数的图象与x轴只有一个
交点,求m的值.
解:(2)①若y=mx2-6x+1为一次函数,则m=0,此时函数与x轴有唯一交点;
②若y=mx2-6x+1为二次函数,则Δ=36-4m=0,
解得m=9.
综上可得m=0或9.
17
19
例、如图以40m/s的速度将小球沿与地面成50°角的方向击出时,小球的飞行路线将是一条抛物线。如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系
h=
–
5t?+20t。
①小球从飞出到落地要用多少时间?
②小球的飞行高度能否达到15m?如果能,求出飞行时间.
③小球的飞行高度能否达到20m?如果能,求出飞行时间.
④小球的飞行高度能否达到20.5m?为什么
h=-5t2+20t
18
19
课堂小结
二次函数与一元二次方程
二次函数与一元二次方程的关系
y=ax2+bx+c(a
≠0),当y取定值时就成了一元二次方程;ax2+bx+c=0(a
≠0),右边换成y时就成了二次函数.
二次函数与一元二次方程根的情况
二次函数与x轴的交点个数
判别式
的符号
一元二次方程根的情况
Δ
19
19
2.5.1二次函数与一元二次方程
1
19
回顾与思
复习提问
1、一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=______。
当△﹥0时,方程根的情况是______________;
当△=0时,方程根的情况是______________;
当△﹤0时,方程根的情况是______________。
b2-4ac
有两个不等实数根
有两个相等实数根
没有实数根
2、二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)图像是一条_____,它与x轴的交点有几种可能的情况?
抛物线
三种可能:①两个交点
②一个交点
③没有交点。
2
19
设抛物线y=ax?+bx+c(a≠0)与x轴有两个交点,交点坐标如何计算?
(1)二次函数y=x2-5x的图象与x轴的两个交点
的坐标分别是
.
(0,0),(5,0)
(2)若方程ax2+bx+c=0(a≠0)的两根分别是x1=2,x2=3,则抛物线y=ax2+bx+c与x轴的交点坐标分别是__________________.
(2,0),(3,0)
3
19
(3)
函数y=x2+ax+b的图象如图,则关于x的方程x2+ax+b=0的解是( )
A.
无解
B.
x=1
C.
x=-4
D.
x=-1或x=4
D
从“数”上看:当函数y=x2+ax+b的函数值y=0时,自变量x的值就变成方程x2+ax+b=0的根
从“形”上看:当二次函数y=x2+ax+b与x轴交点横坐标为方程x2+ax+b=0的根。
?
?
4
19
二次函数
的图象如下图,与同伴交流并回答问题.
回顾与思
探究学习
5
19
二次函数y=x2+2x的图象
与x轴有几个交点?
与x轴有2个交点:
(-2,0)和(0,0)
一元二次方程x2+2x=0
有几个根?
解:x(x+2)=0
∴
x1=-2,x2=0
方程的根是-2和0
6
19
二次函数y=x2-2x+1
的图象与x轴有几个交点?
与x轴有1个交点:
(1,0)
一元二次方程x2-2x+1=0
有几个根?
解:
(x-1)2=0
∴
x1=x2=1
方程的根是1
7
19
二次函数y=x2-2x+2
的图象与x轴有几个交点?
与x轴没有交点
一元二次方程x2-2x+2=0
有几个根?
没有实数根
解:∵△=(-2)2-4×1×2
=-4﹤0
∴
原方程无实根
8
19
归纳总结:
二次函数y=ax2+bx+c的图象和x轴交点
一元二次方程ax2+bx+c=0的根
一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
二次函数y=ax2+bx+c的图象和x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根.
有两个交点
有一个交点
没有交点
有两个相等
的实数根
没有实数根
b2-4ac
>
0
b2-4ac
=
0
b2-4ac
<
0
有两个不相等
的实数根
9
19
所以二次函数与一元二次方程关系密切.
例如,已知二次函数y
=
x2-4x的值为3,求自变量x的值,可以解一元二次方程x2-4x=3(即x2-4x-3=0).
反过来,解方程x2-4x-3=0
又可以看作已知二次函数
y
=
x2-4x-3
的值为0,求自变量x的值.
10
19
(1)抛物线y=x2+3x+2与x轴的交点个数是
(
)
A.
3
B.
2
C.
1
D.
0
(2)抛物线y=2x2+8x+m与x轴只有一个公共点,
则m的值是________.
(3)若抛物线y=ax2+bx+c,当
a>0,c<0时,图象与x轴
的交点情况是
(
)
A.无交点
B.只有一个交点
C.有两个交点
D.不能确定
回顾与思
课堂练习
11
19
(4)(中考)二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①abc<0;
②方程ax2+bx+c=0的根为x1=-1,x2=3;
③当x>1时,y随x值的增大而减小;
④当y>0时,-1<x<3.
其中正确的说法是
(
)
A.①
B.①②
C.①②③
D.①②③④
O
x
y
1
3
-1
12
19
(5)
二次函数y=kx2-2x-1的图象与x轴有交点,则k的取值范围是(
)
A.
k>-1
B.
k≥-1且k≠0
C.
k≥-1
D.
k>-1且k≠0
变式1:已知函数y=(k-3)x2+2x+1的图象与
x轴有交点,求k的取值范围.
变式2:若函数y=mx2+(m+2)x+
m+1的图象与x轴只有一个交点,那么m的值为_________.
13
19
(6)若a>0,b>0,c>0,△>0,那么抛物线y=ax2+bx+c
经过
象限.
一、二、三
(7)若二次函数y=ax2+bx+c的函数值恒为正,则需满足
;
若二次函数y=ax2+bx+c的函数值恒为负,则需满足
.
14
19
(8)如图,函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C.
(1)图象与x轴交点的坐标
是______________
与y轴的交点坐标是_______
(-1,0)和(3,0)
(0,-3)
(2)当x=_______时,y=0;
方程x2-2x-3=0的解是_______;
-1或3
x1=-1,x2=3
15
19
(3)当x满足_____________时,y<0;
当x满足_____________时,y>0;
(4)x2-2x-3<0的解集是___________;
x2-2x-3>0的解集是___________
-1<x<3
x<-1或x>3
-1<x<3
x<-1或x>3
16
19
(9)
已知函数y=mx2-6x+1(m为常数).
(1)求证:无论m为何值,该函数的图象与y轴总有一个固定交点;
(2)若该函数的图象与x轴只有一个
交点,求m的值.
解:(2)①若y=mx2-6x+1为一次函数,则m=0,此时函数与x轴有唯一交点;
②若y=mx2-6x+1为二次函数,则Δ=36-4m=0,
解得m=9.
综上可得m=0或9.
17
19
例、如图以40m/s的速度将小球沿与地面成50°角的方向击出时,小球的飞行路线将是一条抛物线。如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系
h=
–
5t?+20t。
①小球从飞出到落地要用多少时间?
②小球的飞行高度能否达到15m?如果能,求出飞行时间.
③小球的飞行高度能否达到20m?如果能,求出飞行时间.
④小球的飞行高度能否达到20.5m?为什么
h=-5t2+20t
18
19
课堂小结
二次函数与一元二次方程
二次函数与一元二次方程的关系
y=ax2+bx+c(a
≠0),当y取定值时就成了一元二次方程;ax2+bx+c=0(a
≠0),右边换成y时就成了二次函数.
二次函数与一元二次方程根的情况
二次函数与x轴的交点个数
判别式
的符号
一元二次方程根的情况
Δ
19
19
