人教版八年级上册 11.3.2多边形及其内角和学案(解析版)
文档属性
| 名称 | 人教版八年级上册 11.3.2多边形及其内角和学案(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 434.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 23:10:50 | ||
图片预览



文档简介
多边形的内角和与外角和
1.
多边形的相关概念
(1)多边形的定义:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
(2)内角:多边形相邻两边组成的角叫做它的内角.
(3)外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角
(4)对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
(5)凸多边形:如果整个多边形都在其任何一边所在直线的同一侧的多边形.
?
2.
内角和与外角和
如下图,边形的内角和为,多边形的外角和都是.
3.
正多边形
正多边形:各个角相等,且各条边都相等的多边形叫做正多边形.
考点:1.
对角线条数;2.内角和与外角和;3.
正多边形
重难点:
1.
n边形形的对角线:一个顶点有条对角线,共有条对角线.
2.
要计算正多边形的内角度数,除了可以拿内角和()除以边数(n)以外,还可以通过利用外角和()除以边数(n),得到一个顶点处外角的度数,再拿180减去它即可.
易错点:每个多边形在其一个顶点处对应的外角也都只有一个,它们的和等于.
题模一:对角线条数
例1.1.1
若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A.7
B.10
C.35
D.70
例1.1.2
若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是__________边形
例1.1.3
从一个9边形的某个顶点出发,分别连接这个点与其他顶点可以把这个9边形分割成三角形的个数是____个.
例1.1.4
观察下面图形,并回答问题.
(1)四边形有_______条对角线,五边形有_______条对角线,六边形有_______条对角线;
(2)根据规律七边形有_______条对角线,n边形有___________条对角线.
例1.1.5
一个多边形的对角线的条数与它的边数相等,这个多边形是______边形
题模二:内角和与外角和
例1.2.1
一个多边形从某一个顶点出发截去一个角后所形成的新的多边形的内角和是1980°,则原多边形的边数为(
)
A.11或12
B.12或13
C.13或14
D.12或13或14
题模三:正多边形
例1.3.1
已知一个正多边形的每个外角等于60°,则这个正多边形是( )
A.正五边形
B.正六边形
C.正七边形
D.正八边形
例1.3.2
已知正n边形的一个内角为135°,则边数n的值是( )
A.6
B.7
C.8
D.10
例1.3.3
如图所示,小华从A点出发,沿直线前进10米后左转24,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
A.140米
B.150米
C.160米
D.240米
随练1.1
如果一个多边形的边数增加倍后,它的内角和是,那么原来多边形的边数是______
随练1.2
一个多边形的每一个内角都是140°,那么,从这个多边形的一个顶点出发的对角线的条数是_______
随练1.3
一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5
B.5或6
C.5或7
D.5或6或7
随练1.4
将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=32°,那么∠1+∠2=____度.
随练1.5
请总结规律,完成下表:
拓展1
下列说法中错误的有(
)
①各边都相等的多边形是正多边形.②多边形的外角和是指多边形所有外角相加的和.③四个内角均为直角的四边形是正四边形.④多边形的内角和与外角和均与边数有关.⑤正多边形的内角度数与边数无关.⑥多边形的内角和与外角和加起来,应为边数与180°的乘积.
A.2个
B.3个
C.4个
D.5个
拓展2
一个多边形,把一个顶点与其它各顶点连接起来,把这个多边形分成了12个三角形,则这个多边形的边数__________
拓展3
一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7
B.7或8
C.8或9
D.7或8或9
拓展4
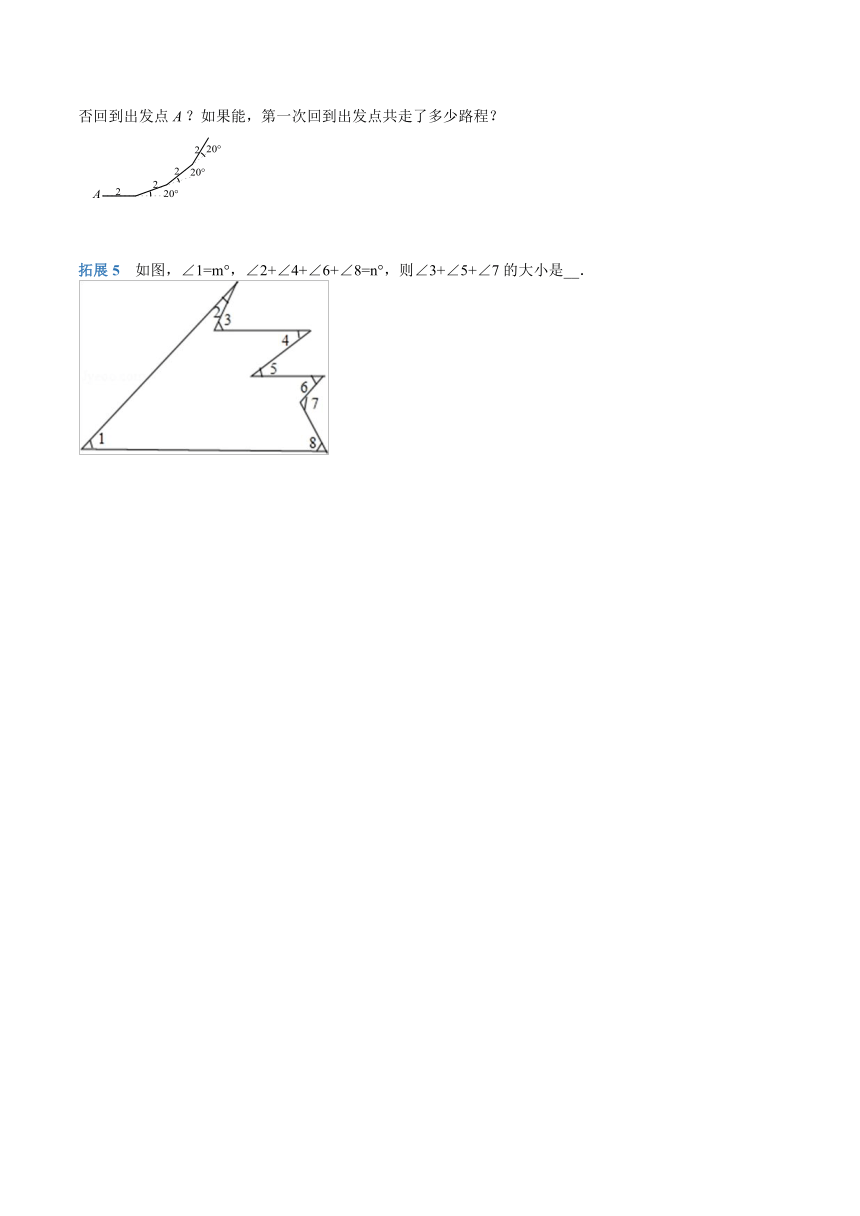
如图,小明从点出发,向前走米,左拐,再向前走米,再左拐,如此下去,小明能否回到出发点?如果能,第一次回到出发点共走了多少路程?
拓展5
如图,∠1=m°,∠2+∠4+∠6+∠8=n°,则∠3+∠5+∠7的大小是__.
答案解析
多边形的内角和与外角和
题模一:对角线条数
例1.1.1
【答案】C
【解析】∵一个正n边形的每个内角为144°,
∴144n=180×(n﹣2),解得:n=10.
这个正n边形的所有对角线的条数是:==35.
例1.1.2
【答案】13
【解析】该题考查的是多边形对角线计算公式.
从一个多边形的一个顶点出发,最多可以引条对角线,(n为多边形边数).
本题中,设这个多边形是n边形.
代入公式,得,
∴.
例1.1.3
【答案】7
【解析】从一个9边形的某个顶点出发,分别连接这个点与其他顶点可以把这个9边形分割成三角形的个数是7个
例1.1.4
【答案】(1)2;5;9,(2)14;
【解析】(1)四边形有2条对角线;五边形有5条对角线;六边形有9条对角线;
(2)七边形有14条对角线,n边形有条对角线.
例1.1.5
【答案】5
【解析】设多边形有条边,则根据题意可列:,解得,(舍)
故多边形的边数为5
题模二:内角和与外角和
例1.2.1
【答案】C
【解析】该题考查的是多边形的角度计算.
多边形内角和公式为,外角度数和为定值,
本题中,,解得
而多边形从某一个顶点出发截去一个角,边数有两种可能,一种是边数不变,一种是边数减少1条,所以原来的多边形边数可能是13或14,故答案是C.
题模三:正多边形
例1.3.1
【答案】B
【解析】设所求正n边形边数为n,
则60°?n=360°,
解得n=6.
故正多边形的边数是6.
故选B.
例1.3.2
【答案】C
【解析】本题考查了多边形的外角,利用多边形的边数等于外角和除以每一个外角的度数是常用的方法,求出多边形的每一个外角的度数是解题的关键.
根据多边形的相邻的内角与外角互为邻补角求出每一个外角的度数,再根据多边形的边数等于外角和除以每一个外角的度数进行计算即可得解.
∵正n边形的一个内角为135°,
∴正n边形的一个外角为180°-135°=45°,
n=360°÷45°=8.
故选C.
例1.3.3
【答案】B
【解析】∵多边形的外角和为360°,而每一个外角为24°,
∴多边形的边数为360°÷24°=15,
∴小明一共走了:15×10=150米.
随练1.1
【答案】
【解析】设原来多边形的边数是n,则,解得
随练1.2
【答案】6
【解析】由于一个多边形的每一个内角都是140°,因此其外角都是40°,则这个多边形的边数为,因此从九边形的每一个顶点出发的对角线的条数为
随练1.3
【答案】D
【解析】本题考查了多边形的内角和定理,理解分三种情况是关键.
首先求得内角和为720°的多边形的边数,即可确定原多边形的边数.
设内角和为720°的多边形的边数是n,则(n-2)?180=720,
解得:n=6.
则原多边形的边数为5或6或7.
故选:D.
随练1.4
【答案】70
【解析】
∵∠3=32°,正三角形的内角是60°,正四边形的内角是90°,正五边形的内角是108°,
∴∠4=180°-60°-32°=88°,
∴∠5+∠6=180°-88°=92°,
∴∠5=180°-∠2-108°??????
①,
∠6=180°-90°-∠1=90°-∠1
②,
∴①+②得,180°-∠2-108°+90°-∠1=92°,
即∠1+∠2=70°.
故答案为:70°.
随练1.5
【答案】见下表:
【解析】n边形过一个顶点可作条对角线,而n边形共有n个顶点,则共可作条对角线,而这条对角线中,有一半是重复计算的,抛去重复的这一半对角线,共有条对角线.
拓展1
【答案】D
【解析】只有⑥是正确的,其余说法均错误
拓展2
【答案】
【解析】从边形的一个顶点作对角线,把这个n边形分成个三角形.根据题意可知,这个多边形的边数是
拓展3
【答案】D
【解析】设内角和为1080°的多边形的边数是n,则(n﹣2)?180°=1080°,解得:n=8.
则原多边形的边数为7或8或9.
拓展4
【答案】能回到出发点,第一次回到出发点共走了.
【解析】根据题意可知,小明所走的路线为一个正多边形,其边数为,即左拐18次后回到出发点.因此小明从点A出发,第一次回到出发点共走了(m).
拓展5
【答案】m°+n°
【解析】如图,连结AB、BC、CD.
∵(∠3+∠9+∠10)+(∠5+∠11+∠12)+(∠7+∠13+∠14)=180°×3=540°,
∴(∠3+∠5+∠7)+(∠9+∠10+∠11+∠12+∠13+∠14)=540°,
∴∠3+∠5+∠7=540°﹣(∠9+∠10+∠11+∠12+∠13+∠14),
∵五边形ABCDE的内角和为(5﹣2)×180°=540°,
∴540°=∠1+∠2+∠9+∠10+∠4+∠11+∠12+∠6+∠13+∠14+∠8
=(∠1+∠2+∠4+∠6+∠8)+(∠9+∠10+∠11+∠12+∠13+∠14)
=(m°+n°)+(∠9+∠10+∠11+∠12+∠13+∠14),
∴∠9+∠10+∠11+∠12+∠13+∠14=540°﹣(m°+n°).
∴∠3+∠5+∠7=540°﹣[540°﹣(m°+n°)]=m°+n°.
0
1.
多边形的相关概念
(1)多边形的定义:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
(2)内角:多边形相邻两边组成的角叫做它的内角.
(3)外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角
(4)对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
(5)凸多边形:如果整个多边形都在其任何一边所在直线的同一侧的多边形.
?
2.
内角和与外角和
如下图,边形的内角和为,多边形的外角和都是.
3.
正多边形
正多边形:各个角相等,且各条边都相等的多边形叫做正多边形.
考点:1.
对角线条数;2.内角和与外角和;3.
正多边形
重难点:
1.
n边形形的对角线:一个顶点有条对角线,共有条对角线.
2.
要计算正多边形的内角度数,除了可以拿内角和()除以边数(n)以外,还可以通过利用外角和()除以边数(n),得到一个顶点处外角的度数,再拿180减去它即可.
易错点:每个多边形在其一个顶点处对应的外角也都只有一个,它们的和等于.
题模一:对角线条数
例1.1.1
若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A.7
B.10
C.35
D.70
例1.1.2
若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是__________边形
例1.1.3
从一个9边形的某个顶点出发,分别连接这个点与其他顶点可以把这个9边形分割成三角形的个数是____个.
例1.1.4
观察下面图形,并回答问题.
(1)四边形有_______条对角线,五边形有_______条对角线,六边形有_______条对角线;
(2)根据规律七边形有_______条对角线,n边形有___________条对角线.
例1.1.5
一个多边形的对角线的条数与它的边数相等,这个多边形是______边形
题模二:内角和与外角和
例1.2.1
一个多边形从某一个顶点出发截去一个角后所形成的新的多边形的内角和是1980°,则原多边形的边数为(
)
A.11或12
B.12或13
C.13或14
D.12或13或14
题模三:正多边形
例1.3.1
已知一个正多边形的每个外角等于60°,则这个正多边形是( )
A.正五边形
B.正六边形
C.正七边形
D.正八边形
例1.3.2
已知正n边形的一个内角为135°,则边数n的值是( )
A.6
B.7
C.8
D.10
例1.3.3
如图所示,小华从A点出发,沿直线前进10米后左转24,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
A.140米
B.150米
C.160米
D.240米
随练1.1
如果一个多边形的边数增加倍后,它的内角和是,那么原来多边形的边数是______
随练1.2
一个多边形的每一个内角都是140°,那么,从这个多边形的一个顶点出发的对角线的条数是_______
随练1.3
一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5
B.5或6
C.5或7
D.5或6或7
随练1.4
将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=32°,那么∠1+∠2=____度.
随练1.5
请总结规律,完成下表:
拓展1
下列说法中错误的有(
)
①各边都相等的多边形是正多边形.②多边形的外角和是指多边形所有外角相加的和.③四个内角均为直角的四边形是正四边形.④多边形的内角和与外角和均与边数有关.⑤正多边形的内角度数与边数无关.⑥多边形的内角和与外角和加起来,应为边数与180°的乘积.
A.2个
B.3个
C.4个
D.5个
拓展2
一个多边形,把一个顶点与其它各顶点连接起来,把这个多边形分成了12个三角形,则这个多边形的边数__________
拓展3
一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7
B.7或8
C.8或9
D.7或8或9
拓展4
如图,小明从点出发,向前走米,左拐,再向前走米,再左拐,如此下去,小明能否回到出发点?如果能,第一次回到出发点共走了多少路程?
拓展5
如图,∠1=m°,∠2+∠4+∠6+∠8=n°,则∠3+∠5+∠7的大小是__.
答案解析
多边形的内角和与外角和
题模一:对角线条数
例1.1.1
【答案】C
【解析】∵一个正n边形的每个内角为144°,
∴144n=180×(n﹣2),解得:n=10.
这个正n边形的所有对角线的条数是:==35.
例1.1.2
【答案】13
【解析】该题考查的是多边形对角线计算公式.
从一个多边形的一个顶点出发,最多可以引条对角线,(n为多边形边数).
本题中,设这个多边形是n边形.
代入公式,得,
∴.
例1.1.3
【答案】7
【解析】从一个9边形的某个顶点出发,分别连接这个点与其他顶点可以把这个9边形分割成三角形的个数是7个
例1.1.4
【答案】(1)2;5;9,(2)14;
【解析】(1)四边形有2条对角线;五边形有5条对角线;六边形有9条对角线;
(2)七边形有14条对角线,n边形有条对角线.
例1.1.5
【答案】5
【解析】设多边形有条边,则根据题意可列:,解得,(舍)
故多边形的边数为5
题模二:内角和与外角和
例1.2.1
【答案】C
【解析】该题考查的是多边形的角度计算.
多边形内角和公式为,外角度数和为定值,
本题中,,解得
而多边形从某一个顶点出发截去一个角,边数有两种可能,一种是边数不变,一种是边数减少1条,所以原来的多边形边数可能是13或14,故答案是C.
题模三:正多边形
例1.3.1
【答案】B
【解析】设所求正n边形边数为n,
则60°?n=360°,
解得n=6.
故正多边形的边数是6.
故选B.
例1.3.2
【答案】C
【解析】本题考查了多边形的外角,利用多边形的边数等于外角和除以每一个外角的度数是常用的方法,求出多边形的每一个外角的度数是解题的关键.
根据多边形的相邻的内角与外角互为邻补角求出每一个外角的度数,再根据多边形的边数等于外角和除以每一个外角的度数进行计算即可得解.
∵正n边形的一个内角为135°,
∴正n边形的一个外角为180°-135°=45°,
n=360°÷45°=8.
故选C.
例1.3.3
【答案】B
【解析】∵多边形的外角和为360°,而每一个外角为24°,
∴多边形的边数为360°÷24°=15,
∴小明一共走了:15×10=150米.
随练1.1
【答案】
【解析】设原来多边形的边数是n,则,解得
随练1.2
【答案】6
【解析】由于一个多边形的每一个内角都是140°,因此其外角都是40°,则这个多边形的边数为,因此从九边形的每一个顶点出发的对角线的条数为
随练1.3
【答案】D
【解析】本题考查了多边形的内角和定理,理解分三种情况是关键.
首先求得内角和为720°的多边形的边数,即可确定原多边形的边数.
设内角和为720°的多边形的边数是n,则(n-2)?180=720,
解得:n=6.
则原多边形的边数为5或6或7.
故选:D.
随练1.4
【答案】70
【解析】
∵∠3=32°,正三角形的内角是60°,正四边形的内角是90°,正五边形的内角是108°,
∴∠4=180°-60°-32°=88°,
∴∠5+∠6=180°-88°=92°,
∴∠5=180°-∠2-108°??????
①,
∠6=180°-90°-∠1=90°-∠1
②,
∴①+②得,180°-∠2-108°+90°-∠1=92°,
即∠1+∠2=70°.
故答案为:70°.
随练1.5
【答案】见下表:
【解析】n边形过一个顶点可作条对角线,而n边形共有n个顶点,则共可作条对角线,而这条对角线中,有一半是重复计算的,抛去重复的这一半对角线,共有条对角线.
拓展1
【答案】D
【解析】只有⑥是正确的,其余说法均错误
拓展2
【答案】
【解析】从边形的一个顶点作对角线,把这个n边形分成个三角形.根据题意可知,这个多边形的边数是
拓展3
【答案】D
【解析】设内角和为1080°的多边形的边数是n,则(n﹣2)?180°=1080°,解得:n=8.
则原多边形的边数为7或8或9.
拓展4
【答案】能回到出发点,第一次回到出发点共走了.
【解析】根据题意可知,小明所走的路线为一个正多边形,其边数为,即左拐18次后回到出发点.因此小明从点A出发,第一次回到出发点共走了(m).
拓展5
【答案】m°+n°
【解析】如图,连结AB、BC、CD.
∵(∠3+∠9+∠10)+(∠5+∠11+∠12)+(∠7+∠13+∠14)=180°×3=540°,
∴(∠3+∠5+∠7)+(∠9+∠10+∠11+∠12+∠13+∠14)=540°,
∴∠3+∠5+∠7=540°﹣(∠9+∠10+∠11+∠12+∠13+∠14),
∵五边形ABCDE的内角和为(5﹣2)×180°=540°,
∴540°=∠1+∠2+∠9+∠10+∠4+∠11+∠12+∠6+∠13+∠14+∠8
=(∠1+∠2+∠4+∠6+∠8)+(∠9+∠10+∠11+∠12+∠13+∠14)
=(m°+n°)+(∠9+∠10+∠11+∠12+∠13+∠14),
∴∠9+∠10+∠11+∠12+∠13+∠14=540°﹣(m°+n°).
∴∠3+∠5+∠7=540°﹣[540°﹣(m°+n°)]=m°+n°.
0
