人教版数学九年级下册课件:27.1图形的相似(23张)
文档属性
| 名称 | 人教版数学九年级下册课件:27.1图形的相似(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 281.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
图形的相似
知识点、考点回顾:
一、比例:
3.比例中项:若a/b=c/d=bc,则b叫a、c的比例中项.
2.第四比例项:若a/b=c/d,则d叫a、b、c的第四比例项.
1、比例:如果a:b与c:d的比值相等,我们就说
这四个数a,b,c,d成比例,写成比例式a:b=c:d。
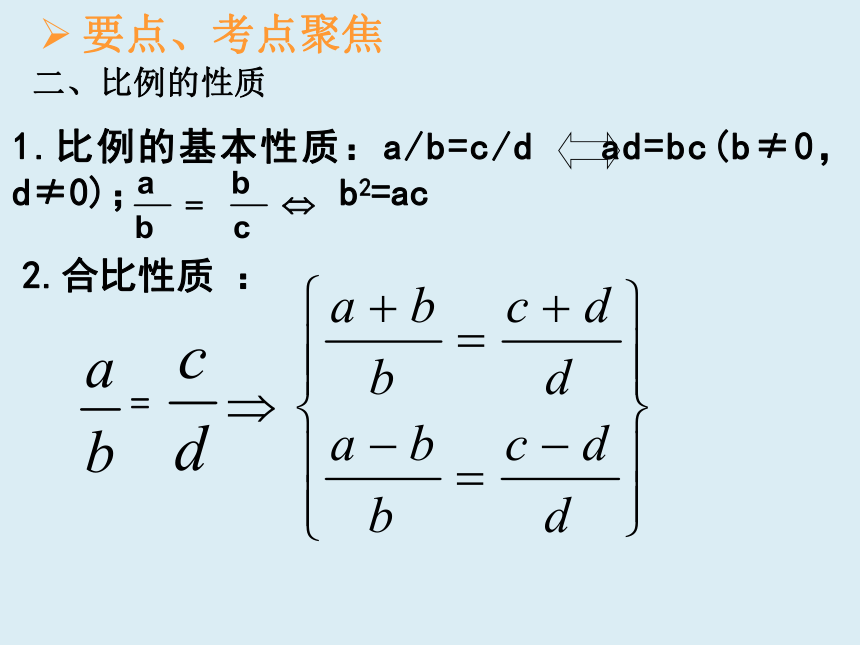
二、比例的性质
1.比例的基本性质:a/b=c/d
ad=bc(b≠0,d≠0);
b2=ac
=
2.合比性质
:
要点、考点聚焦
3.
等比性质:若
=
=…=
(b+d+…+n≠0),那么.
三、比例线段
2.比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段
叫做成比例线段,简称比例线段.
1、线段的比:选用同一长度单位的两条线段的长度的比。
3.
等比性质:若
=
=…=
(b+d+…+n≠0),那么.
四、黄金分割:
1、黄金分割点:若线段AB上一点C,满足AC/AB=BC/AC,则称点C是AB的黄金分割点。
2、黄金分割比:
3、黄金矩形:宽与长的比等于黄金比的矩形
。
1、相似三角形的定义:
对应角相等,对应边成比例的三角形.
2、探索两个三角形相似的条件:
判定定理1:两角对应相等的两个三角形相似.
判定定理2:两边对应成比例且夹角相等,两个三角形相似.
判定定理3:三边对应成比例的两个三角形相似
五、相似多边形:各角相等,各边对应成比例的两个多边形。(相似的符号是“∽”)对应边的比叫做相似比。
一、相似三角形的性质:
(1)相似三角形对应角相等,对应边成比例.
(2)相似三角形对应高线之比、对应中线之比和
对应角平分线之比分别都等于相似比.
(3)相似三角形周长之比等于相似比.
(4)相似三角形面积之比等于相似比的平方.
知识点、考点回顾:
注意:相似多边形也具有以上性质。
典型例题解析
【例1】在比例尺是1∶38000的南京交通游览图上,玄武湖隧道长约7cm,它的实际长度约为
(
)
A.0.266km
B.2.66km
C.26.6km
D.266km
【例2】设2a-3b=0,则
=
,
=
B
【例3】若4是x和
的比例中项,则x=
典型例题解析
【例4】如果
=
=
≠0,那么
的值是(
)
A.7
B.8
C.9
D.10
【解析】方法1:设x=2k,y=3k,z=4k,代入求值,这种方法比较适用,故选C.
方法2:利用比例的性质,
C
【例5】已知三个数1,
,
,
请你再添上一个
(只填一个)数,使它们能构成一个比例式,则这个数是
【解析】这是一道开放型考题,旨在考查学生的发散思维
能力,由于题中没有明确这四个数的顺序,因此所添的数有很大的灵活性,根据比例的基本性质:设这个数
为x则有
典型例题解析
【例6】
(1)把10厘米的线段进行黄金分割,则较长的线段的长是_______厘米.
(2)把一根2米的钢丝弯成一个矩形框,并使矩形框的宽与长之比成黄金比,则这个矩形的面积是__________.
(3)设P、Q是线段AB上的两个黄金分割点,且PQ=a,则AB=___________.
典型例题解析
2.如图所示,在平行四边形ABCD中,G是BC延长线上一点,AG与BD交于点E,与DC交于点F,则图中相似三角形共有(
)
A.3对
B.4对
C.5对
D.6对
【例7】
1、下列命题正确的是
(
)
A.所有的直角三角形都相似
B.所有的等腰三角形都相似
C.所有的等腰直角三角形都相似
D.以上结论都不正确
C
D
【例8】已知,如图所示的,△ABC中,AD⊥BC于D,下列条件:①∠B+∠DAC=90°②∠B=∠DAC③CD/AD=AC/AB④AB2=BD·BC能得到∠BAC=90°的有
(
)
A.0个
B.1个
C.2个
D.3个
C
典型例题解析:
典型例题解析:
【例9】如图所示,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,DE//BC,那么在下列三角形中,与△ABC相似的三角形是_______________.
÷
【例10】如图,正方形ABCD边长是2,BE=CE,MN=1,线段MN的两端在CD、AD上滑动,当DM=
时,
△ABE与以D、M、N为顶点的三角形相似。
典型例题解析:
【例10】如图所示,梯形ABCD中,AB∥CD,∠B=90°,MN∥AB,AB=6,BC=4,CD=3,设DM=x.
(1)设MN=y,用x的代数式表示y.
(2)设梯形MNCD的面积为S,用x的代数式表示S.
(3)若梯形MNCD的面积S等于梯形ABCD的面积的13,求DM.
典型例题解析
【例10】如图所示,梯形ABCD中,AB∥CD,∠B=90°,
MN∥AB,AB=6,BC=4,CD=3,设DM=x.
(1)设MN=y,用x的代数式表示y.
(2)设梯形MNCD的面积为S,用x
的代数式表示S.
【解析】(1)过D作DE⊥AB于E点交MN于F,MN=MF+FN=MF+3,在Rt△DAE中,AD=
由MN∥AB
(2)MN∥AB
∴S=
(DC+MN)·DF=
x2+
x(0<x<5)
(3)S梯ABCD=
(3+6)×4=18
∴S梯MNCD=
x1=-5+5
,x2=-5-5
<0(舍去).
即DM=-5+5
.
【例10】如图所示,梯形ABCD中,AB∥CD,∠B=90°,
MN∥AB,AB=6,BC=4,CD=3,设DM=x.
(1)y=3/5x+3(0(2)
(3)若梯形MNCD的面积S等于梯
形ABCD的面积的1/3,求DM.
∴S=
x2+
x(0<x<5)
【例12】已知,如图所示的四边形ABCD为菱形,AF⊥BC于F,
(1)求证:AD2=
DE·DB.
(2)过点E作EG⊥AF交AB于点G,若线段BE,DE(BE<DE)的长是方程x2-3mx+2m2=0(m>0)的两个根,且菱形ABCD的面积为
,求EG的长.
【解析】(1)证等积式,首先想到化成比例,但式子有1/2,应想到菱形的性质:对角线互相垂直平分,故连接AC交BD于O点,即BD=2DO,所以AD2=DE·DO
【例12】已知,如图所示的四边形ABCD为菱形,AF⊥BC于F,
(1)求证:AD2=
DE·DB.
(2)过点E作EG⊥AF交AB于点G,若线段BE,DE(BE<DE)的长是方程x2-3mx+2m2=0(m>0)的两个根,且菱形ABCD的面积为
,求EG的长.
典型例题解析
【解析】(1)要证
就得找三角形相似,即要证△ADE与△AOD相似,而∠EAD=90°,
AO⊥BD,所以△ADE∽△OAD.
(2)解方程DE=2m,BE=m,由AD∥BC
由AD2=
DE·BD
AD=
m
∴AE=
=m
∴EF=
m
AF=
m
则S菱ABCD=AF·BC=
m=2,m=-2<0(舍)
由GE⊥AF
GF∥BC
14、已知:在等腰梯形
ABCD中,AD∥BC,直线MN是梯形的对称轴,P是MN上的一点.直线BP交直线DC于F,交CE于E,且CE∥AB.
(1)若点P在梯形的内部,如图①.求证:BP
=PE·PF
;
(2)若点P在梯形的外部,如图②,那么(1)的结论是否成立?若成立,请证明;若不成立,请说明理由.
课时训练:
见讲义----基础演练
图形的相似
知识点、考点回顾:
一、比例:
3.比例中项:若a/b=c/d=bc,则b叫a、c的比例中项.
2.第四比例项:若a/b=c/d,则d叫a、b、c的第四比例项.
1、比例:如果a:b与c:d的比值相等,我们就说
这四个数a,b,c,d成比例,写成比例式a:b=c:d。
二、比例的性质
1.比例的基本性质:a/b=c/d
ad=bc(b≠0,d≠0);
b2=ac
=
2.合比性质
:
要点、考点聚焦
3.
等比性质:若
=
=…=
(b+d+…+n≠0),那么.
三、比例线段
2.比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段
叫做成比例线段,简称比例线段.
1、线段的比:选用同一长度单位的两条线段的长度的比。
3.
等比性质:若
=
=…=
(b+d+…+n≠0),那么.
四、黄金分割:
1、黄金分割点:若线段AB上一点C,满足AC/AB=BC/AC,则称点C是AB的黄金分割点。
2、黄金分割比:
3、黄金矩形:宽与长的比等于黄金比的矩形
。
1、相似三角形的定义:
对应角相等,对应边成比例的三角形.
2、探索两个三角形相似的条件:
判定定理1:两角对应相等的两个三角形相似.
判定定理2:两边对应成比例且夹角相等,两个三角形相似.
判定定理3:三边对应成比例的两个三角形相似
五、相似多边形:各角相等,各边对应成比例的两个多边形。(相似的符号是“∽”)对应边的比叫做相似比。
一、相似三角形的性质:
(1)相似三角形对应角相等,对应边成比例.
(2)相似三角形对应高线之比、对应中线之比和
对应角平分线之比分别都等于相似比.
(3)相似三角形周长之比等于相似比.
(4)相似三角形面积之比等于相似比的平方.
知识点、考点回顾:
注意:相似多边形也具有以上性质。
典型例题解析
【例1】在比例尺是1∶38000的南京交通游览图上,玄武湖隧道长约7cm,它的实际长度约为
(
)
A.0.266km
B.2.66km
C.26.6km
D.266km
【例2】设2a-3b=0,则
=
,
=
B
【例3】若4是x和
的比例中项,则x=
典型例题解析
【例4】如果
=
=
≠0,那么
的值是(
)
A.7
B.8
C.9
D.10
【解析】方法1:设x=2k,y=3k,z=4k,代入求值,这种方法比较适用,故选C.
方法2:利用比例的性质,
C
【例5】已知三个数1,
,
,
请你再添上一个
(只填一个)数,使它们能构成一个比例式,则这个数是
【解析】这是一道开放型考题,旨在考查学生的发散思维
能力,由于题中没有明确这四个数的顺序,因此所添的数有很大的灵活性,根据比例的基本性质:设这个数
为x则有
典型例题解析
【例6】
(1)把10厘米的线段进行黄金分割,则较长的线段的长是_______厘米.
(2)把一根2米的钢丝弯成一个矩形框,并使矩形框的宽与长之比成黄金比,则这个矩形的面积是__________.
(3)设P、Q是线段AB上的两个黄金分割点,且PQ=a,则AB=___________.
典型例题解析
2.如图所示,在平行四边形ABCD中,G是BC延长线上一点,AG与BD交于点E,与DC交于点F,则图中相似三角形共有(
)
A.3对
B.4对
C.5对
D.6对
【例7】
1、下列命题正确的是
(
)
A.所有的直角三角形都相似
B.所有的等腰三角形都相似
C.所有的等腰直角三角形都相似
D.以上结论都不正确
C
D
【例8】已知,如图所示的,△ABC中,AD⊥BC于D,下列条件:①∠B+∠DAC=90°②∠B=∠DAC③CD/AD=AC/AB④AB2=BD·BC能得到∠BAC=90°的有
(
)
A.0个
B.1个
C.2个
D.3个
C
典型例题解析:
典型例题解析:
【例9】如图所示,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,DE//BC,那么在下列三角形中,与△ABC相似的三角形是_______________.
÷
【例10】如图,正方形ABCD边长是2,BE=CE,MN=1,线段MN的两端在CD、AD上滑动,当DM=
时,
△ABE与以D、M、N为顶点的三角形相似。
典型例题解析:
【例10】如图所示,梯形ABCD中,AB∥CD,∠B=90°,MN∥AB,AB=6,BC=4,CD=3,设DM=x.
(1)设MN=y,用x的代数式表示y.
(2)设梯形MNCD的面积为S,用x的代数式表示S.
(3)若梯形MNCD的面积S等于梯形ABCD的面积的13,求DM.
典型例题解析
【例10】如图所示,梯形ABCD中,AB∥CD,∠B=90°,
MN∥AB,AB=6,BC=4,CD=3,设DM=x.
(1)设MN=y,用x的代数式表示y.
(2)设梯形MNCD的面积为S,用x
的代数式表示S.
【解析】(1)过D作DE⊥AB于E点交MN于F,MN=MF+FN=MF+3,在Rt△DAE中,AD=
由MN∥AB
(2)MN∥AB
∴S=
(DC+MN)·DF=
x2+
x(0<x<5)
(3)S梯ABCD=
(3+6)×4=18
∴S梯MNCD=
x1=-5+5
,x2=-5-5
<0(舍去).
即DM=-5+5
.
【例10】如图所示,梯形ABCD中,AB∥CD,∠B=90°,
MN∥AB,AB=6,BC=4,CD=3,设DM=x.
(1)y=3/5x+3(0
(3)若梯形MNCD的面积S等于梯
形ABCD的面积的1/3,求DM.
∴S=
x2+
x(0<x<5)
【例12】已知,如图所示的四边形ABCD为菱形,AF⊥BC于F,
(1)求证:AD2=
DE·DB.
(2)过点E作EG⊥AF交AB于点G,若线段BE,DE(BE<DE)的长是方程x2-3mx+2m2=0(m>0)的两个根,且菱形ABCD的面积为
,求EG的长.
【解析】(1)证等积式,首先想到化成比例,但式子有1/2,应想到菱形的性质:对角线互相垂直平分,故连接AC交BD于O点,即BD=2DO,所以AD2=DE·DO
【例12】已知,如图所示的四边形ABCD为菱形,AF⊥BC于F,
(1)求证:AD2=
DE·DB.
(2)过点E作EG⊥AF交AB于点G,若线段BE,DE(BE<DE)的长是方程x2-3mx+2m2=0(m>0)的两个根,且菱形ABCD的面积为
,求EG的长.
典型例题解析
【解析】(1)要证
就得找三角形相似,即要证△ADE与△AOD相似,而∠EAD=90°,
AO⊥BD,所以△ADE∽△OAD.
(2)解方程DE=2m,BE=m,由AD∥BC
由AD2=
DE·BD
AD=
m
∴AE=
=m
∴EF=
m
AF=
m
则S菱ABCD=AF·BC=
m=2,m=-2<0(舍)
由GE⊥AF
GF∥BC
14、已知:在等腰梯形
ABCD中,AD∥BC,直线MN是梯形的对称轴,P是MN上的一点.直线BP交直线DC于F,交CE于E,且CE∥AB.
(1)若点P在梯形的内部,如图①.求证:BP
=PE·PF
;
(2)若点P在梯形的外部,如图②,那么(1)的结论是否成立?若成立,请证明;若不成立,请说明理由.
课时训练:
见讲义----基础演练
