高中信息技术选修1教案-4.1.2 用解析法求解问题的实践-粤教版
文档属性
| 名称 | 高中信息技术选修1教案-4.1.2 用解析法求解问题的实践-粤教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 363.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-01-11 08:24:43 | ||
图片预览

文档简介
教学设计:用解析法求解问题的实践 ——设计数列运算程序
基本信息
课题名称
用解析法求解问题的实践——设计数列运算程序
课时
1个课时
所属教材
目录
新教材 粤教版必修1第四章第4单元第2课
(粤教版 必修模块1:数据与计算
第四章 程序设计基础
4.4运用循环结构描述问题求解过程
4.4.1 for循环的应用)
教学程序语言
Python语言
教学程序工具
Python 3.7
教材分析
本课是在学完for循环课程学习之后开展的实践活动课,培养学生的计算思维能力,灵活运用数学数列知识,应用计算机程序解决数学问题和日常生活中的实际问题,学生第一次参加一场竞赛,在学习时,老师可以引导学生参与基于问题的项目学习,经历建立数据模型、抽象数据、选择解决办法、算法实现、上机调试、问题解决的全过程。
学情分析
在上一节课中,学生学习了for循环语句。学生对这方面的知识有了初步的了解,也对程序设计逐渐显示出了更大的兴趣。然而遇到实际问题时候,学生不容易做出相关的题目,需要补充一些示范或范例材料,帮助学生理解。
教学目标
1.进一步深入学习for循环语句的应用。
2.逐渐掌握一种程序设计语言的基本知识,使用它实现简单的算法。
3.通过解决实际问题,体验程序设计的基本过程或流程,初步感受算法的效率,掌握程序调试与运行的方法。
4.培养竞争意识,力争上游,相互学习,知己知彼,取长补短。
5.收获通过计算机程序解决数学问题带来的喜悦,把已学的数学知识学以致用。
教学
重难点
重点
①算法的设计
②求数学问题解(计算思维)
③数值与计算实现for循环结构的程序
难点
①for循环结构的应用
②把握数据的逻辑关系(信息意识、逻辑思维)把算法描述实现为程序
③程序的调试
教学策略
与
设计说明
让学生在主动参与竞赛,基于项目的学习,实践活动中积累与构建信息技术学科核心素养。在数学数列问题情境中表现其思考问题设计算法的能力和学习品质,提高计算思维能力。
本节课通过循序渐进的几道题目,从完成知识的建构、思维的发展、信息文化的理解等多个方面进行的教学设计。
教学过程
教学环节
(开始--
结束)
教师活动
学生活动
设计意图
一
(1-2分钟)
导入:今天进行一场竞赛,看看大家的表现,同学们加油!
介绍如何打开本竞赛。
这次竞赛班上谁将是最厉害呢?
讨论,准备竞赛。
熟悉竞赛平台如何登入。
了解本次提交“竞赛”的规则,引导学生热身准备接受挑战,培养竞争意识,导入竞赛。
二
(3-4分钟)
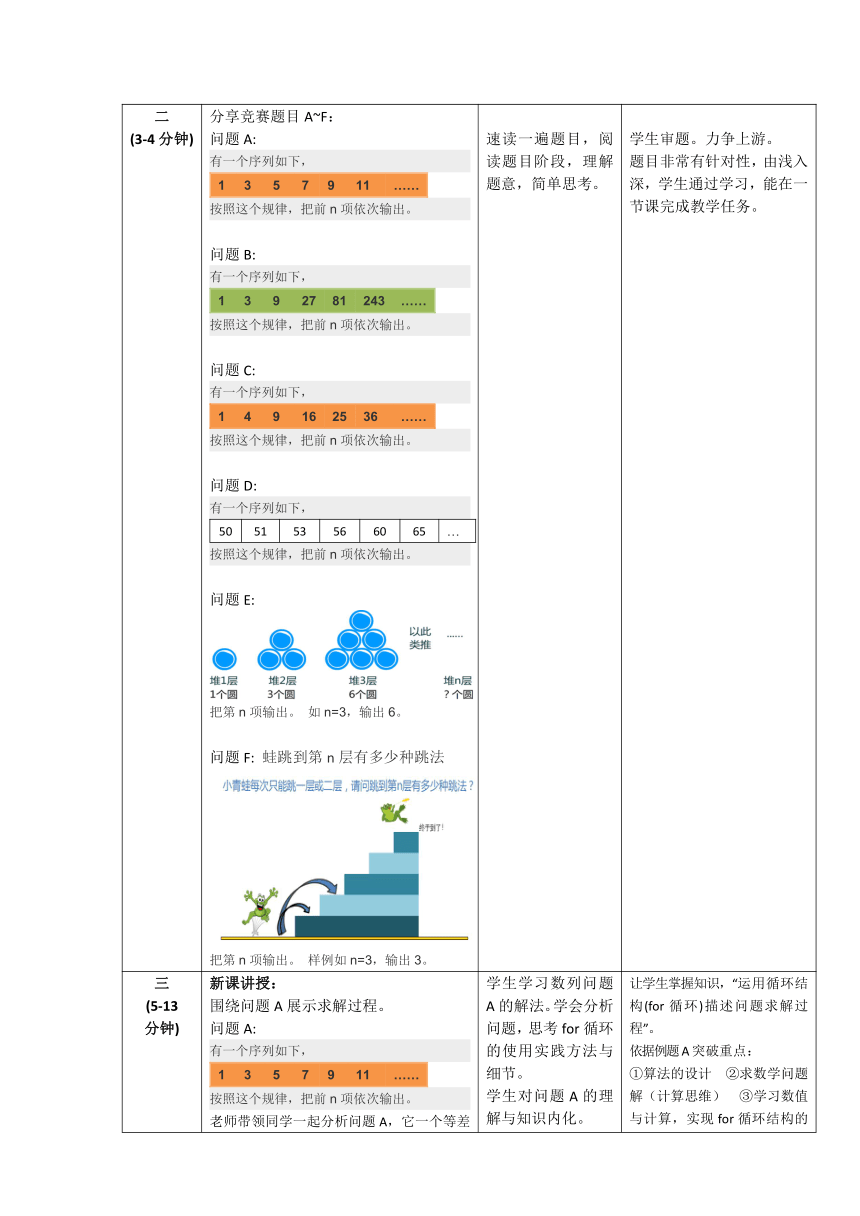
分享竞赛题目A~F:
问题A:
有一个序列如下,
1
3
5
7
9
11
……
按照这个规律,把前n项依次输出。
问题B:
有一个序列如下,
1
3
9
27
81
243
……
按照这个规律,把前n项依次输出。
问题C:
有一个序列如下,
1
4
9
16
25
36
……
按照这个规律,把前n项依次输出。
问题D:
有一个序列如下,
50
51
53
56
60
65
…
按照这个规律,把前n项依次输出。
问题E:
把第n项输出。 如n=3,输出6。
问题F: 蛙跳到第n层有多少种跳法
把第n项输出。 样例如n=3,输出3。
速读一遍题目,阅读题目阶段,理解题意,简单思考。
学生审题。力争上游。
题目非常有针对性,由浅入深,学生通过学习,能在一节课完成教学任务。
三
(5-13
分钟)
新课讲授:
围绕问题A展示求解过程。
问题A:
有一个序列如下,
1
3
5
7
9
11
……
按照这个规律,把前n项依次输出。
老师带领同学一起分析问题A,它一个等差数列,公差是2。
老师介绍该问题可以用通项式与递推式两种方法求解。
展示两种解法,并简单分析各方法的优劣。
学生学习数列问题A的解法。学会分析问题,思考for循环的使用实践方法与细节。
学生对问题A的理解与知识内化。
让学生掌握知识,“运用循环结构(for循环)描述问题求解过程”。
依据例题A突破重点:
①算法的设计 ②求数学问题解(计算思维) ③学习数值与计算,实现for循环结构的程序。
四
(14-40
分钟)
激烈比赛阶段
同学们开始竞赛,思考问题,设计算法,创设代码阶段,完成竞赛题目A~问题F共6题。
依据学生提交情况,适当的分析题目,给出相应的提示。
重点讲授分析最后一题问题F。
这题实际上是斐波那契数列应用题。
提示:先推算出前面的4或5层时的跳法,看看能不能看出规律,大胆设想数列。
怎么理解这个规律?假设现在要跳到第n层,思考:蛙从哪些层出发可以跳一次就能到该层,从而推出有多少个方法可以到达这第n层。
应用自顶而下,把大问题简化为子问题的方法去想。
如层数一共是5层,如何简化呢?我们试试把跳5层的跳法原问题分解为跳3层的子问题和4层的子问题。
5变成4是把哪边的拆呢?是拆分靠近地面的第一层还是快到终点的最后的一层?
明显如果拆分地面第一层,原问题不得简化。
我们接着试把快到终点的最后一层拆分,5层变4层,5层原问题的答案可以从子问题4层中推算。
蛙最后一跳可以从第几层出发呢?这时,蛙只跳一次直接到第5层?答案是:从第3层出发,只跳一次(2层)或者是从第4层出发,只跳一次(1层)即到达终点5。这两种出发的线路加起来的跳法就是总跳法。
我们于是可以把求跳5层的跳法原问题分解为跳3层的子问题和跳4层的子问题。
学生解答出类似的题,问题B问题C。
问题D和E就要知识迁移了,灵活梳理数理逻辑的关系。遇到不懂可讨论,借鉴老师的提示,求出题目的答案。
设计6题,帮助学生突破难点:
①for循环结构的应用
②把算法描述实现为程序
③程序的调试
在数学数列问题情境中表现其思考问题设计算法的能力和学习品质,提高计算思维能力。
五
(40-45
分钟)
总结本课学习内容,点评竞赛的完成情况。
学生认知自己的学习情况,归纳总结,反思,升华,内化。
回应本课程的主题,深化对数组与计算的理解。
课堂小结
学生通过竞赛训练,掌握所学的知识。以练为主,学生可以讨论,找出办法。
教学设计
流程图
导入——>展示问题——>新课讲授(求解过程)——>
学生竞赛——>总结点评竞赛情况
教学资源
竞赛题目与分析,
教学评价
教师通过设计竞赛环境,学生积极参与竞赛训练,经过简单复习,把原知识迁移并拓展新知识,从而突破本节课的教学重点。
竞赛时,实时地动态刷屏看到学生的做题情况,更有针对性地开展教学。启发学生深入思考,理解数理逻辑关系,巧妙突破难点。
作者结合新课标要求,教学围绕新课程理念,灵活应用新教材,语言通顺流利,亲和力强,打造了教学的亮点;搭建竞赛系统,实现提交与评价功能。题目设计有层次有梯度,能力培养符合学生的认知规律,从了解理解到类比再到探究,层层推进;一节课下来,我们能感受到学生动手能力强,大部分同学能完成学习任务。教学目标围绕信息技术核心素养进行设置,作者是一位善于引领学生思考、培养学生兴趣爱好、务实进取的优秀教师。
附:学生做题情况汇总
基本信息
课题名称
用解析法求解问题的实践——设计数列运算程序
课时
1个课时
所属教材
目录
新教材 粤教版必修1第四章第4单元第2课
(粤教版 必修模块1:数据与计算
第四章 程序设计基础
4.4运用循环结构描述问题求解过程
4.4.1 for循环的应用)
教学程序语言
Python语言
教学程序工具
Python 3.7
教材分析
本课是在学完for循环课程学习之后开展的实践活动课,培养学生的计算思维能力,灵活运用数学数列知识,应用计算机程序解决数学问题和日常生活中的实际问题,学生第一次参加一场竞赛,在学习时,老师可以引导学生参与基于问题的项目学习,经历建立数据模型、抽象数据、选择解决办法、算法实现、上机调试、问题解决的全过程。
学情分析
在上一节课中,学生学习了for循环语句。学生对这方面的知识有了初步的了解,也对程序设计逐渐显示出了更大的兴趣。然而遇到实际问题时候,学生不容易做出相关的题目,需要补充一些示范或范例材料,帮助学生理解。
教学目标
1.进一步深入学习for循环语句的应用。
2.逐渐掌握一种程序设计语言的基本知识,使用它实现简单的算法。
3.通过解决实际问题,体验程序设计的基本过程或流程,初步感受算法的效率,掌握程序调试与运行的方法。
4.培养竞争意识,力争上游,相互学习,知己知彼,取长补短。
5.收获通过计算机程序解决数学问题带来的喜悦,把已学的数学知识学以致用。
教学
重难点
重点
①算法的设计
②求数学问题解(计算思维)
③数值与计算实现for循环结构的程序
难点
①for循环结构的应用
②把握数据的逻辑关系(信息意识、逻辑思维)把算法描述实现为程序
③程序的调试
教学策略
与
设计说明
让学生在主动参与竞赛,基于项目的学习,实践活动中积累与构建信息技术学科核心素养。在数学数列问题情境中表现其思考问题设计算法的能力和学习品质,提高计算思维能力。
本节课通过循序渐进的几道题目,从完成知识的建构、思维的发展、信息文化的理解等多个方面进行的教学设计。
教学过程
教学环节
(开始--
结束)
教师活动
学生活动
设计意图
一
(1-2分钟)
导入:今天进行一场竞赛,看看大家的表现,同学们加油!
介绍如何打开本竞赛。
这次竞赛班上谁将是最厉害呢?
讨论,准备竞赛。
熟悉竞赛平台如何登入。
了解本次提交“竞赛”的规则,引导学生热身准备接受挑战,培养竞争意识,导入竞赛。
二
(3-4分钟)
分享竞赛题目A~F:
问题A:
有一个序列如下,
1
3
5
7
9
11
……
按照这个规律,把前n项依次输出。
问题B:
有一个序列如下,
1
3
9
27
81
243
……
按照这个规律,把前n项依次输出。
问题C:
有一个序列如下,
1
4
9
16
25
36
……
按照这个规律,把前n项依次输出。
问题D:
有一个序列如下,
50
51
53
56
60
65
…
按照这个规律,把前n项依次输出。
问题E:
把第n项输出。 如n=3,输出6。
问题F: 蛙跳到第n层有多少种跳法
把第n项输出。 样例如n=3,输出3。
速读一遍题目,阅读题目阶段,理解题意,简单思考。
学生审题。力争上游。
题目非常有针对性,由浅入深,学生通过学习,能在一节课完成教学任务。
三
(5-13
分钟)
新课讲授:
围绕问题A展示求解过程。
问题A:
有一个序列如下,
1
3
5
7
9
11
……
按照这个规律,把前n项依次输出。
老师带领同学一起分析问题A,它一个等差数列,公差是2。
老师介绍该问题可以用通项式与递推式两种方法求解。
展示两种解法,并简单分析各方法的优劣。
学生学习数列问题A的解法。学会分析问题,思考for循环的使用实践方法与细节。
学生对问题A的理解与知识内化。
让学生掌握知识,“运用循环结构(for循环)描述问题求解过程”。
依据例题A突破重点:
①算法的设计 ②求数学问题解(计算思维) ③学习数值与计算,实现for循环结构的程序。
四
(14-40
分钟)
激烈比赛阶段
同学们开始竞赛,思考问题,设计算法,创设代码阶段,完成竞赛题目A~问题F共6题。
依据学生提交情况,适当的分析题目,给出相应的提示。
重点讲授分析最后一题问题F。
这题实际上是斐波那契数列应用题。
提示:先推算出前面的4或5层时的跳法,看看能不能看出规律,大胆设想数列。
怎么理解这个规律?假设现在要跳到第n层,思考:蛙从哪些层出发可以跳一次就能到该层,从而推出有多少个方法可以到达这第n层。
应用自顶而下,把大问题简化为子问题的方法去想。
如层数一共是5层,如何简化呢?我们试试把跳5层的跳法原问题分解为跳3层的子问题和4层的子问题。
5变成4是把哪边的拆呢?是拆分靠近地面的第一层还是快到终点的最后的一层?
明显如果拆分地面第一层,原问题不得简化。
我们接着试把快到终点的最后一层拆分,5层变4层,5层原问题的答案可以从子问题4层中推算。
蛙最后一跳可以从第几层出发呢?这时,蛙只跳一次直接到第5层?答案是:从第3层出发,只跳一次(2层)或者是从第4层出发,只跳一次(1层)即到达终点5。这两种出发的线路加起来的跳法就是总跳法。
我们于是可以把求跳5层的跳法原问题分解为跳3层的子问题和跳4层的子问题。
学生解答出类似的题,问题B问题C。
问题D和E就要知识迁移了,灵活梳理数理逻辑的关系。遇到不懂可讨论,借鉴老师的提示,求出题目的答案。
设计6题,帮助学生突破难点:
①for循环结构的应用
②把算法描述实现为程序
③程序的调试
在数学数列问题情境中表现其思考问题设计算法的能力和学习品质,提高计算思维能力。
五
(40-45
分钟)
总结本课学习内容,点评竞赛的完成情况。
学生认知自己的学习情况,归纳总结,反思,升华,内化。
回应本课程的主题,深化对数组与计算的理解。
课堂小结
学生通过竞赛训练,掌握所学的知识。以练为主,学生可以讨论,找出办法。
教学设计
流程图
导入——>展示问题——>新课讲授(求解过程)——>
学生竞赛——>总结点评竞赛情况
教学资源
竞赛题目与分析,
教学评价
教师通过设计竞赛环境,学生积极参与竞赛训练,经过简单复习,把原知识迁移并拓展新知识,从而突破本节课的教学重点。
竞赛时,实时地动态刷屏看到学生的做题情况,更有针对性地开展教学。启发学生深入思考,理解数理逻辑关系,巧妙突破难点。
作者结合新课标要求,教学围绕新课程理念,灵活应用新教材,语言通顺流利,亲和力强,打造了教学的亮点;搭建竞赛系统,实现提交与评价功能。题目设计有层次有梯度,能力培养符合学生的认知规律,从了解理解到类比再到探究,层层推进;一节课下来,我们能感受到学生动手能力强,大部分同学能完成学习任务。教学目标围绕信息技术核心素养进行设置,作者是一位善于引领学生思考、培养学生兴趣爱好、务实进取的优秀教师。
附:学生做题情况汇总
同课章节目录
- 第一章 揭开计算机解决问题的神秘面纱
- 1.1 计算机解决问题的过程
- 1.2 算法和算法的描述
- 第二章 程序设计基础
- 2.1 VB语言急程序开发环境
- 2.2 程序的顺序结构
- 2.3 程序的选择结构
- 2.4 程序的循环结构
- 2.5 模块化程序设计
- 第三章 可视化编程
- 3.1 可视化编程的概念与方法
- 3.2 程序调试的方法
- 第四章 算法与程序实现
- 4.1 用解析法设计程序
- 4.2 用穷举法设计程序
- 4.3 查找算法设计
- 4.4 排序算法设计
- 4.5 递归算法与递归程序
- 第五章 面向对象的程序设计
- 5.1 面向对象程序设计的基本思想
- 5.2 面向对象程序设计的基本概念
- 5.3 面向对象的功能实现
- 第六章 程序设计实践
- 6.1 多媒体应用程序设计
- 6.2 数据库管理软件的开发
