人教版九年级数学上册教学设计:24.4弧长和扇形面积
文档属性
| 名称 | 人教版九年级数学上册教学设计:24.4弧长和扇形面积 |

|
|
| 格式 | zip | ||
| 文件大小 | 590.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 23:12:46 | ||
图片预览


文档简介
九年级数学上册教学设计
课题
24.4弧长和扇形面积
教学
目标
1.理解弧长和扇形面积公式,并会计算弧长和扇形的面积.
2.掌握圆锥的侧面积计算公式,并会应用公式解决问题.
3.通过用弧长及扇形面积公式解决实际问题,让学生体验数学与人类生活的密切联系.
教学
重点
1.推导弧长及扇形面积计算公式的过程.
2.掌握弧长及扇形面积计算公式,会用公式解决问题.
教学
难点
推导弧长及扇形面积计算公式的过程.
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、弧长的计算公式.
1.1°的圆心角所对的弧长是多少?n°的圆心角呢?
在半径为R的圆中,因为360°的圆心角所对的弧长就是圆周长C=2πR,所以1°的圆心角所对的弧长是,即.于是n°的圆心角所对的弧长为.
二、扇形面积的计算公式.
如图,由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.可以发现,扇形的面积除了与圆的半径有关外还与组成扇形的圆心角的大小有关,圆心角越大,扇形面积也就越大.怎样计算圆半径为R,圆心角为n°的扇形面积呢?
1.如何计算圆的面积?圆面积可以看作是多少度的圆心角所对的扇形的面积?1°的圆心角所对的扇形面积是多少?n°的圆心角呢?
在半径为R的圆中,因为360°的圆心角所对的扇形的面积就是圆面积S=πR2,所以1°的扇形面积是,于是圆心角为n°的扇形面积是S扇形=.
例1.
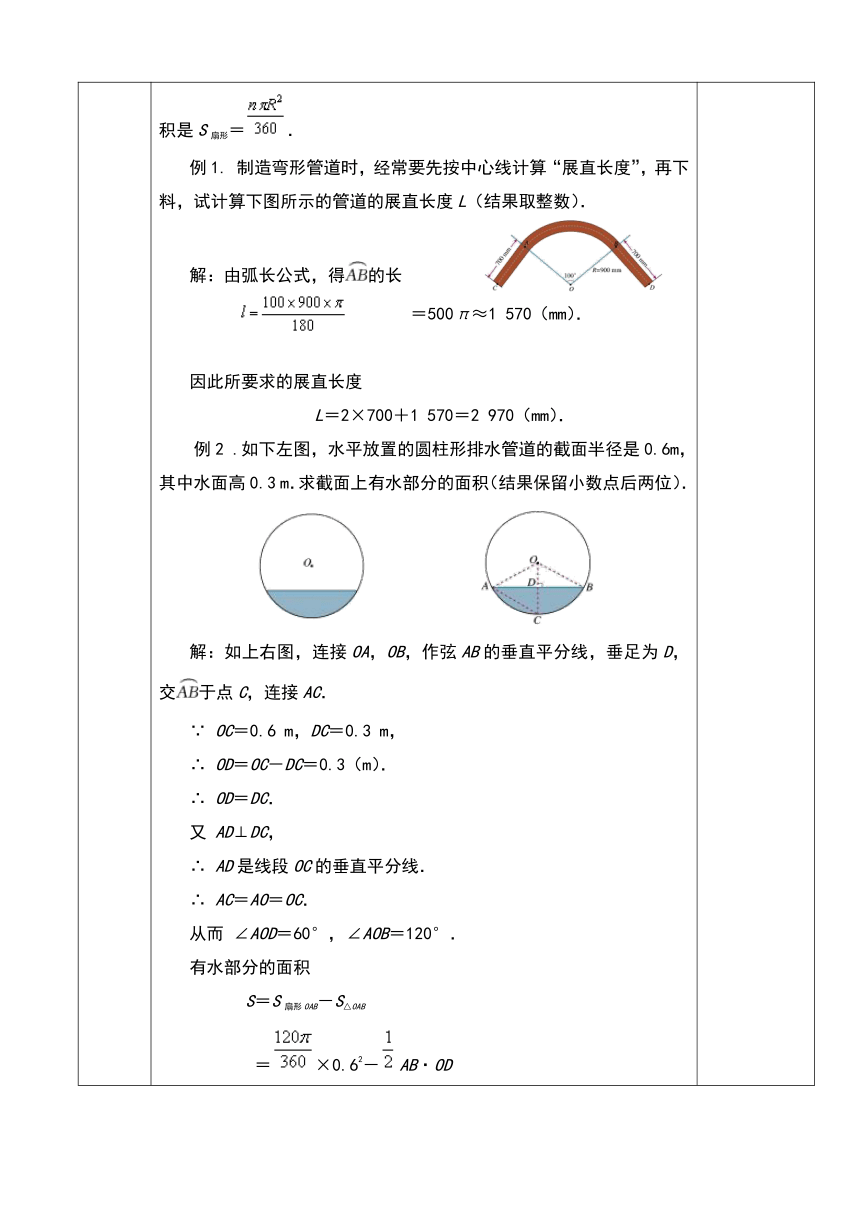
制造弯形管道时,经常要先按中心线计算“展直长度”,再下料,试计算下图所示的管道的展直长度L(结果取整数).
解:由弧长公式,得的长
=500π≈1
570(mm).
因此所要求的展直长度
L=2×700+1
570=2
970(mm).
例2
.如下左图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3
m.求截面上有水部分的面积(结果保留小数点后两位).
解:如上右图,连接OA,OB,作弦AB的垂直平分线,垂足为D,交于点C,连接AC.
∵
OC=0.6
m,DC=0.3
m,
∴
OD=OC-DC=0.3(m).
∴
OD=DC.
又
AD⊥DC,
∴
AD是线段OC的垂直平分线.
∴
AC=AO=OC.
从而
∠AOD=60°,∠AOB=120°.
有水部分的面积
S=S扇形OAB-S△OAB
=×0.62-AB·OD
=0.12π-×0.6×0.3
≈0.22(m2).
三、圆锥的侧面公式.
圆锥是由一个底面和一个侧面围成的几何体,我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.
1.圆锥的侧面展开图是什么图形?如何计算圆锥的侧面积?如何计算圆锥的全面积?
(1)如图,沿一条母线将圆锥侧面剪开并展平,容易得到,圆锥的侧面展开图是一个扇形.
(2)设圆锥的母线长为l,底面圆的半径为r,那么这个扇形的半径为l,扇形的弧长为2πr,因此圆锥的侧面积为πrl,圆锥的全面积为πr(r+l).
例3.
制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算下图中管道的展直长度,即的长(结果精确到0.1
mm).
分析:要求管道的展直长度,即求的长,根根弧长公式l=可求得的长,其中n为圆心角,R为半径.
解:R=40mm,n=110.
∴的长=πR=×40π≈76.8mm.
因此,管道的展直长度约为76.8mm.
例4.
圣诞节将近,某家商店正在制作圣诞节的圆锥形纸帽.已知纸帽的底面周长为58cm,高为20cm,要制作20顶这样的纸帽至少要用多少平方厘米的纸?(结果精确到0.1cm2
)
分析:根据题意,要求纸帽的面积,即求圆锥的侧面积.现在已知底面圆的周长,从中可求出底面圆的半径,从而可求出扇形的弧长.在高h、底面圆的半径r、母线l组成的直角三角形中,根据勾股定理求出母线l,代入S侧=πrl中即可.
解:设纸帽的底面半径为r
cm,母线长为l
cm,则r=
l=≈22.03cm,
S圆锥侧=πrl≈×58×22.03=638.87cm2.
638.87×20=12
777.4cm2.
所以,至少需要12
777.4cm2的纸.
课堂练习
1.如图,ABC为等腰直角三角形木板,为直角,米.将该木板绕着点B沿箭头所示方向旋转,使点A、B、C在同一直线上.则点A从开始到结束所走过的路径长度为(
)
A.(米)
B.(米)
C.(米)
D.(米)
2.已知圆锥的底面面积为,母线长为,则圆锥的侧面积是(
)
A.
B.
C.
D.
3.在圆心角为的扇形中,半径,则扇形的面积是(
)
A.
B.
C.
D.
4.已知的斜边,一条直角边,分别以以下三边所在直线为轴旋转一周所得几何体的表面积最大的为(
)
A.AB
B.AC
C.BC
D.不确定
5.如图,从一块直径为2的圆形铁皮上剪出一个圆心角为的扇形CAB,且点C,A,B都在上,将此扇形围成一个圆锥,则该圆锥底面圆的半径是(
)
A.
B.
C.
D.
6.扇形的圆心角是,弧长为,则扇形的面积为(
)
A.
B.
C.
D.
7.如图,是某同学制作的一个圆锥形纸帽的示意图,则围成这个纸帽的纸的面积为________.
8.的圆心角所对的弧长是,则此弧所在圆的半径是_____CM.
9.圆锥的底面半径为,高为,则它的表面积为________.(结果保留π)
10.如图,在矩形中,,,点E,F分别为AB,BC的中点.以点E为圆心、AB的长为直径作半圆,以点F为圆心、BC的长为直径作半圆,则阴影部分的面积为________.
11.用一张面积为的正方形硬纸片围成一个圆柱的侧面,这个圆柱的底面直径是________(精确到).
激趣导入,引入主题。
板
书
设
计
一、弧长的计算公式.
二、扇形面积的计算公式.
三、探索圆锥的侧面公式.
教
学
反
思
课题
24.4弧长和扇形面积
教学
目标
1.理解弧长和扇形面积公式,并会计算弧长和扇形的面积.
2.掌握圆锥的侧面积计算公式,并会应用公式解决问题.
3.通过用弧长及扇形面积公式解决实际问题,让学生体验数学与人类生活的密切联系.
教学
重点
1.推导弧长及扇形面积计算公式的过程.
2.掌握弧长及扇形面积计算公式,会用公式解决问题.
教学
难点
推导弧长及扇形面积计算公式的过程.
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、弧长的计算公式.
1.1°的圆心角所对的弧长是多少?n°的圆心角呢?
在半径为R的圆中,因为360°的圆心角所对的弧长就是圆周长C=2πR,所以1°的圆心角所对的弧长是,即.于是n°的圆心角所对的弧长为.
二、扇形面积的计算公式.
如图,由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.可以发现,扇形的面积除了与圆的半径有关外还与组成扇形的圆心角的大小有关,圆心角越大,扇形面积也就越大.怎样计算圆半径为R,圆心角为n°的扇形面积呢?
1.如何计算圆的面积?圆面积可以看作是多少度的圆心角所对的扇形的面积?1°的圆心角所对的扇形面积是多少?n°的圆心角呢?
在半径为R的圆中,因为360°的圆心角所对的扇形的面积就是圆面积S=πR2,所以1°的扇形面积是,于是圆心角为n°的扇形面积是S扇形=.
例1.
制造弯形管道时,经常要先按中心线计算“展直长度”,再下料,试计算下图所示的管道的展直长度L(结果取整数).
解:由弧长公式,得的长
=500π≈1
570(mm).
因此所要求的展直长度
L=2×700+1
570=2
970(mm).
例2
.如下左图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3
m.求截面上有水部分的面积(结果保留小数点后两位).
解:如上右图,连接OA,OB,作弦AB的垂直平分线,垂足为D,交于点C,连接AC.
∵
OC=0.6
m,DC=0.3
m,
∴
OD=OC-DC=0.3(m).
∴
OD=DC.
又
AD⊥DC,
∴
AD是线段OC的垂直平分线.
∴
AC=AO=OC.
从而
∠AOD=60°,∠AOB=120°.
有水部分的面积
S=S扇形OAB-S△OAB
=×0.62-AB·OD
=0.12π-×0.6×0.3
≈0.22(m2).
三、圆锥的侧面公式.
圆锥是由一个底面和一个侧面围成的几何体,我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.
1.圆锥的侧面展开图是什么图形?如何计算圆锥的侧面积?如何计算圆锥的全面积?
(1)如图,沿一条母线将圆锥侧面剪开并展平,容易得到,圆锥的侧面展开图是一个扇形.
(2)设圆锥的母线长为l,底面圆的半径为r,那么这个扇形的半径为l,扇形的弧长为2πr,因此圆锥的侧面积为πrl,圆锥的全面积为πr(r+l).
例3.
制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算下图中管道的展直长度,即的长(结果精确到0.1
mm).
分析:要求管道的展直长度,即求的长,根根弧长公式l=可求得的长,其中n为圆心角,R为半径.
解:R=40mm,n=110.
∴的长=πR=×40π≈76.8mm.
因此,管道的展直长度约为76.8mm.
例4.
圣诞节将近,某家商店正在制作圣诞节的圆锥形纸帽.已知纸帽的底面周长为58cm,高为20cm,要制作20顶这样的纸帽至少要用多少平方厘米的纸?(结果精确到0.1cm2
)
分析:根据题意,要求纸帽的面积,即求圆锥的侧面积.现在已知底面圆的周长,从中可求出底面圆的半径,从而可求出扇形的弧长.在高h、底面圆的半径r、母线l组成的直角三角形中,根据勾股定理求出母线l,代入S侧=πrl中即可.
解:设纸帽的底面半径为r
cm,母线长为l
cm,则r=
l=≈22.03cm,
S圆锥侧=πrl≈×58×22.03=638.87cm2.
638.87×20=12
777.4cm2.
所以,至少需要12
777.4cm2的纸.
课堂练习
1.如图,ABC为等腰直角三角形木板,为直角,米.将该木板绕着点B沿箭头所示方向旋转,使点A、B、C在同一直线上.则点A从开始到结束所走过的路径长度为(
)
A.(米)
B.(米)
C.(米)
D.(米)
2.已知圆锥的底面面积为,母线长为,则圆锥的侧面积是(
)
A.
B.
C.
D.
3.在圆心角为的扇形中,半径,则扇形的面积是(
)
A.
B.
C.
D.
4.已知的斜边,一条直角边,分别以以下三边所在直线为轴旋转一周所得几何体的表面积最大的为(
)
A.AB
B.AC
C.BC
D.不确定
5.如图,从一块直径为2的圆形铁皮上剪出一个圆心角为的扇形CAB,且点C,A,B都在上,将此扇形围成一个圆锥,则该圆锥底面圆的半径是(
)
A.
B.
C.
D.
6.扇形的圆心角是,弧长为,则扇形的面积为(
)
A.
B.
C.
D.
7.如图,是某同学制作的一个圆锥形纸帽的示意图,则围成这个纸帽的纸的面积为________.
8.的圆心角所对的弧长是,则此弧所在圆的半径是_____CM.
9.圆锥的底面半径为,高为,则它的表面积为________.(结果保留π)
10.如图,在矩形中,,,点E,F分别为AB,BC的中点.以点E为圆心、AB的长为直径作半圆,以点F为圆心、BC的长为直径作半圆,则阴影部分的面积为________.
11.用一张面积为的正方形硬纸片围成一个圆柱的侧面,这个圆柱的底面直径是________(精确到).
激趣导入,引入主题。
板
书
设
计
一、弧长的计算公式.
二、扇形面积的计算公式.
三、探索圆锥的侧面公式.
教
学
反
思
同课章节目录
