4.3.1角课件(共20张ppt)
图片预览



文档简介
(共20张PPT)
§4.3.1
角
授课人:赵佳峰
珍珠山乡冲河学校
找
出
下
列
图
片
中
哪
部
分
具
有
角
的
形
象
请你找角
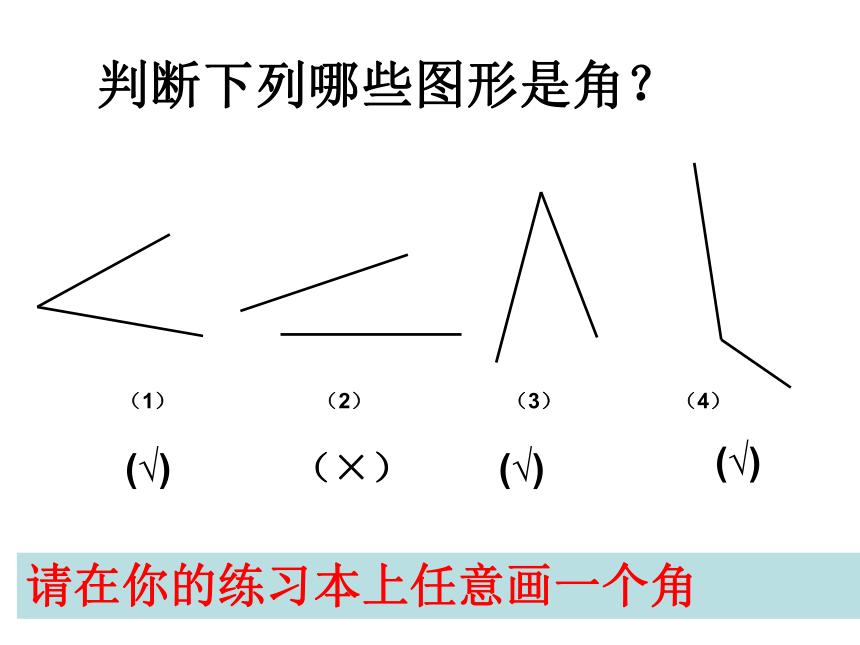
判断下列哪些图形是角?
(√)
(√)
(√)
(×)
(1)
(2)
(3)
(4)
请在你的练习本上任意画一个角
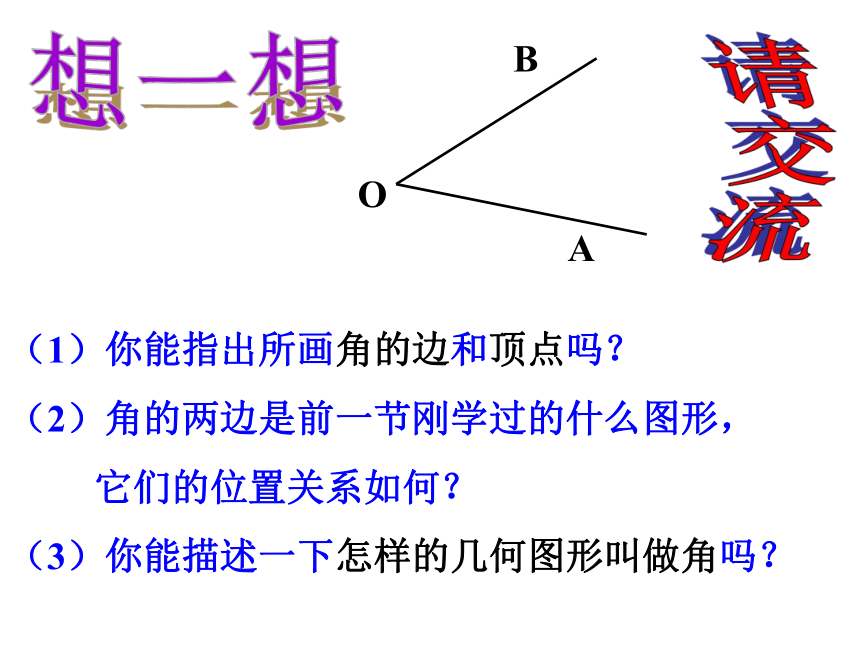
(1)你能指出所画角的边和顶点吗?
(2)角的两边是前一节刚学过的什么图形,
它们的位置关系如何?
(3)你能描述一下怎样的几何图形叫做角吗?
O
A
B
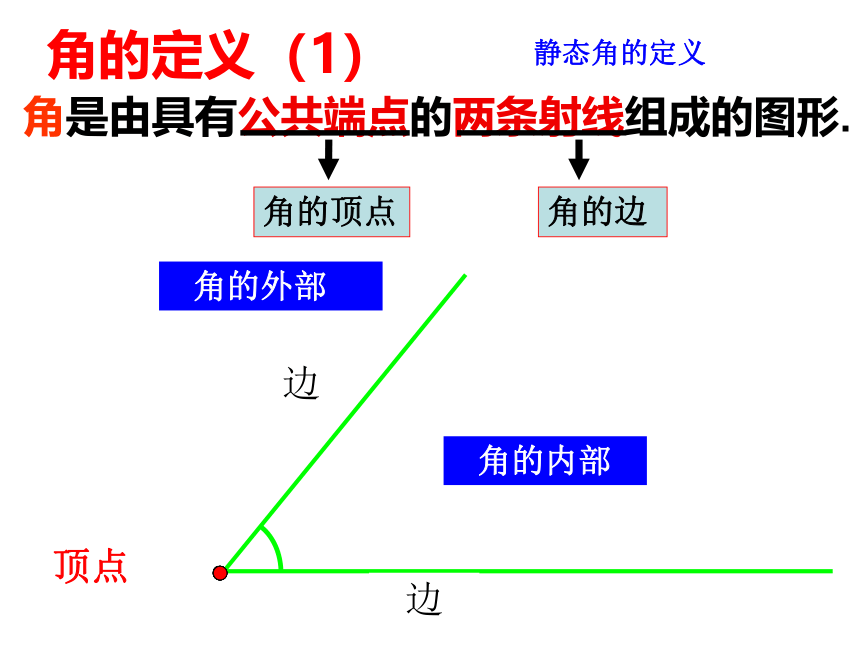
角是由具有公共端点的两条射线组成的图形.
顶点
射线
射线
边
边
角的定义(1)
静态角的定义
角的顶点
角的边
角的内部
角的外部
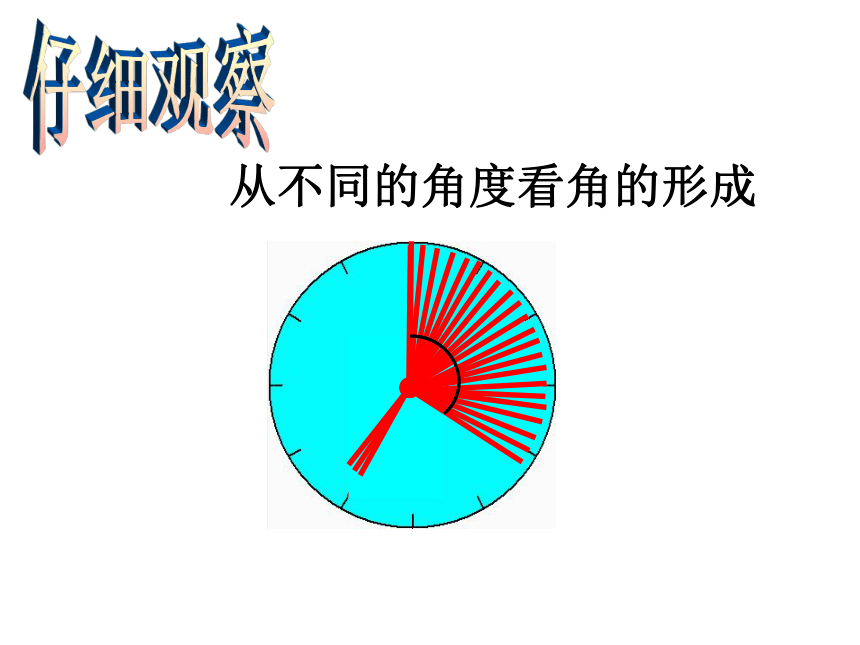
从不同的角度看角的形成
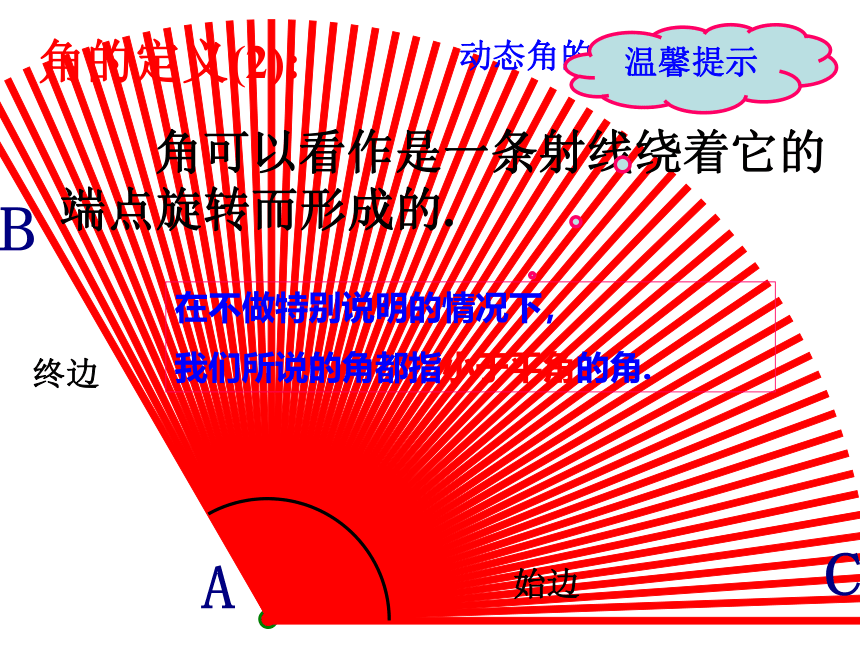
角的定义(2):
动态角的定义
角可以看作是一条射线绕着它的端点旋转而形成的.
温馨提示
在不做特别说明的情况下,
我们所说的角都指小于平角的角.
始边
终边
O
A
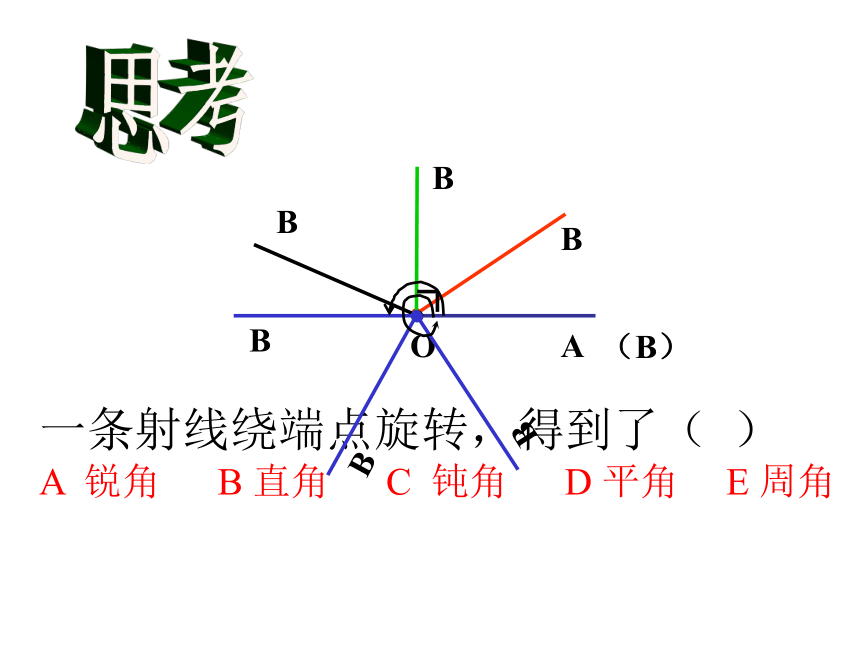
一条射线绕端点旋转,得到了(
)
A
锐角
B
直角
C
钝角
D
平角
E
周角
B
B
B
B
(B)
B
B
判断题:
(1)两条射线组成的图形叫角.
(2)直线是一个平角.
(3)具有公共端点的两条射线组成角.
(4)角的边画得越长,角就越大.
(5)角的两边是两条线段.
(6)18时整,时针和分针成一个平角.
角用符号“∠
”表示,读做“角”.
(1)用三个大写字母表示,但表示顶点的字母一定要写在中间.
如∠AOB或∠BOA
(2)
用一个字母表示角,
如∠O
∠
A
O
B
∠
(3)
用一个数字表示角,在靠近顶点处画上弧线,写上数字.
如∠1
1
(4)用一个希腊字母表示,在靠近顶点处画上弧线,写上希腊字母.
如∠α
α
但必须是以这个字母为顶点的角只有一个.
C
P
O
C
A
①⑥
1.将图中的角表示成下列形式:
①∠APO
②∠AOP
③
OPC
④∠O
⑤∠COP
⑥∠P
其中正确的有
(把你认为正确的序号都填上.)
2.如图,回答下列问题:
C
D
B
A
(1)∠ABD与∠ABC是同一个角吗?
(2)能用一个大写字母表示的角有几个?
(3)以点A为顶点的角有哪几个?以点D为顶点的角呢?
(4)图中共有多少个角?分别是哪些角?
(4)解:7个,分别是
∠ABC、
∠ACB
∠BAC、
∠BAD、
∠CAD
∠ADB、
∠ADC
(3)解:
表示方法
图标
记法
注意事项
用三个大写的字母表示
用一个顶点的字母表示
用一个数字表示
C
A
B
ABC
o
1
α
顶点字母在中间
顶点处只有
一个角时
在靠近顶点处
画弧线,
注上数字
或希腊字母
1
o
α
用希腊字母表示
1.
能用哪种方法表示下面闪烁的角
A
B
1
O
(1)
∠1
(2)
∠AOB
(3)
∠O
2.
将图中已标出的角用不同的方法表示出来,
并填入下表.
∠1
∠3
∠4
∠BCA
∠ABC
A
D
C
B
E
5
4
3
1
2
∠BCE
∠2
∠BAE
∠DAB
∠5
B
经常用量角量一个角的度数,度、分、秒是常用的角的度量单位,把一个周角分成360份,一份就是1°,把1°分成60份,一份就是1′,把1
分成60份,一份就是1″,以度、分、秒为单位的角的度量制就是角度制。
谈谈你对角度制的认识
1周角=
°
1平角=
°
1
°=
′
,
1′=
″
(1)23°31
′25
″+
42°37
′56
″;
(2)
42°31
′56
″-
23°37
′25
″;
(3)
23°31
′25
″×3;
(4)21°17
′22″×5;
选做题:如图,在∠AOB内部引射线,
(1)从同一顶点O处引出1条射线,则可以得到
个角;
(2)从同一顶点O处引出2条射线,则可以得到
个角;
(3)从同一顶点O处引出3条射线,则可以得到
个角;
(4)从同一顶点O处引出n条射线,则可以得到
个角.
你能解决下列问题吗?试一试
C
D
B
A
O
小结
角的定义
角的表示方法
本节课你有什么收获?
还有什么困惑?
必做题:
练习册
P126:7、10
红角和蓝角到底谁大谁小?
角的大小与边的长短无关!
§4.3.1
角
授课人:赵佳峰
珍珠山乡冲河学校
找
出
下
列
图
片
中
哪
部
分
具
有
角
的
形
象
请你找角
判断下列哪些图形是角?
(√)
(√)
(√)
(×)
(1)
(2)
(3)
(4)
请在你的练习本上任意画一个角
(1)你能指出所画角的边和顶点吗?
(2)角的两边是前一节刚学过的什么图形,
它们的位置关系如何?
(3)你能描述一下怎样的几何图形叫做角吗?
O
A
B
角是由具有公共端点的两条射线组成的图形.
顶点
射线
射线
边
边
角的定义(1)
静态角的定义
角的顶点
角的边
角的内部
角的外部
从不同的角度看角的形成
角的定义(2):
动态角的定义
角可以看作是一条射线绕着它的端点旋转而形成的.
温馨提示
在不做特别说明的情况下,
我们所说的角都指小于平角的角.
始边
终边
O
A
一条射线绕端点旋转,得到了(
)
A
锐角
B
直角
C
钝角
D
平角
E
周角
B
B
B
B
(B)
B
B
判断题:
(1)两条射线组成的图形叫角.
(2)直线是一个平角.
(3)具有公共端点的两条射线组成角.
(4)角的边画得越长,角就越大.
(5)角的两边是两条线段.
(6)18时整,时针和分针成一个平角.
角用符号“∠
”表示,读做“角”.
(1)用三个大写字母表示,但表示顶点的字母一定要写在中间.
如∠AOB或∠BOA
(2)
用一个字母表示角,
如∠O
∠
A
O
B
∠
(3)
用一个数字表示角,在靠近顶点处画上弧线,写上数字.
如∠1
1
(4)用一个希腊字母表示,在靠近顶点处画上弧线,写上希腊字母.
如∠α
α
但必须是以这个字母为顶点的角只有一个.
C
P
O
C
A
①⑥
1.将图中的角表示成下列形式:
①∠APO
②∠AOP
③
OPC
④∠O
⑤∠COP
⑥∠P
其中正确的有
(把你认为正确的序号都填上.)
2.如图,回答下列问题:
C
D
B
A
(1)∠ABD与∠ABC是同一个角吗?
(2)能用一个大写字母表示的角有几个?
(3)以点A为顶点的角有哪几个?以点D为顶点的角呢?
(4)图中共有多少个角?分别是哪些角?
(4)解:7个,分别是
∠ABC、
∠ACB
∠BAC、
∠BAD、
∠CAD
∠ADB、
∠ADC
(3)解:
表示方法
图标
记法
注意事项
用三个大写的字母表示
用一个顶点的字母表示
用一个数字表示
C
A
B
ABC
o
1
α
顶点字母在中间
顶点处只有
一个角时
在靠近顶点处
画弧线,
注上数字
或希腊字母
1
o
α
用希腊字母表示
1.
能用哪种方法表示下面闪烁的角
A
B
1
O
(1)
∠1
(2)
∠AOB
(3)
∠O
2.
将图中已标出的角用不同的方法表示出来,
并填入下表.
∠1
∠3
∠4
∠BCA
∠ABC
A
D
C
B
E
5
4
3
1
2
∠BCE
∠2
∠BAE
∠DAB
∠5
B
经常用量角量一个角的度数,度、分、秒是常用的角的度量单位,把一个周角分成360份,一份就是1°,把1°分成60份,一份就是1′,把1
分成60份,一份就是1″,以度、分、秒为单位的角的度量制就是角度制。
谈谈你对角度制的认识
1周角=
°
1平角=
°
1
°=
′
,
1′=
″
(1)23°31
′25
″+
42°37
′56
″;
(2)
42°31
′56
″-
23°37
′25
″;
(3)
23°31
′25
″×3;
(4)21°17
′22″×5;
选做题:如图,在∠AOB内部引射线,
(1)从同一顶点O处引出1条射线,则可以得到
个角;
(2)从同一顶点O处引出2条射线,则可以得到
个角;
(3)从同一顶点O处引出3条射线,则可以得到
个角;
(4)从同一顶点O处引出n条射线,则可以得到
个角.
你能解决下列问题吗?试一试
C
D
B
A
O
小结
角的定义
角的表示方法
本节课你有什么收获?
还有什么困惑?
必做题:
练习册
P126:7、10
红角和蓝角到底谁大谁小?
角的大小与边的长短无关!
